数据结构: 线段树
文章目录
- 简介
- 树节点
- 建树
- 区间查询
- 单点改变
- 区间改变
- 例题
- 博客示例完整代码
简介
线段树是一种二叉树形数据结构,1977年由Jon Louis Bentley发明, 上面的每个节点用来存储区间和线段,特别的,叶子节点存储长度为1的线段,即一个值。对区间的查找和节点的更新都可以在 O ( l o g N ) O(logN) O(logN)的内完成。其空间复杂度为 O ( 4 N ) O(4N) O(4N)。运用延迟更新技术,其可用于区间的更新,时间复杂度仍然为 O ( l o g N ) O(logN) O(logN)。
树节点
const int MAXN = 100000;
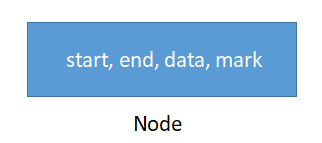
struct Node
{
int start;
int end;
int data;
int mark;
}segment_tree[MAXN*4];
- start:区间的起始
- end:区间的结束
- data:节点的值, 代表区间[start, end)的属性 (根据实际问题赋值)
- mark:用于延迟更新(根据实际问题赋值)
- 注意1: 这篇博客遵循传统的 S T L STL STL库,区间采用前开后闭的形式,即 [ s t a r t , e n d ) [start, end) [start,end)。
- 注意2: 这篇博客我们采用查询区间[a,b)的最小值, 单点改变某个值,对区间[a,b)的每个数加减一个数进行举例。
建树
线段树的建立是一个线段的二分过程。采用递归建树的方法。
- 示意图:对数组 [4,1,2,3,5,6] 建树
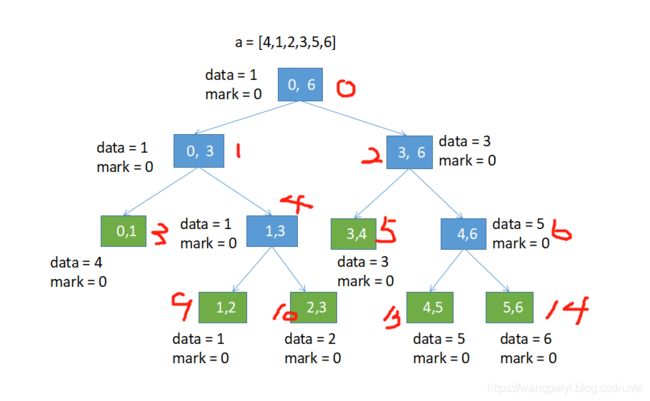
- 绿色节点: 叶子节点。
- 节点中数字: 代表区间。
- 红色数字: 代表节点存在于实际数组中的下标。
- data: 该区间最小值,data值的计算是自底向上的。
- mark:区间改变量。因为只是初始化,因此改变量为0。
- 代码:根据示意图,很容易写出递归建树代码
void build(int start, int end, int index)
{
/*
[start, end): 目前建立节点负责区间负责区间
index: 目前建立结点在segment_tree数组中的下标
使用方式: 如针对数据: int base[6] = {4,1,2,3,5,6};
调用build(0, 6, 0)完成建树
*/
// 赋值区间
segment_tree[index].start = start ;
segment_tree[index].end = end;
// 如果已经到了叶子节点
if(segment_tree[index].start == segment_tree[index].end - 1)
{
segment_tree[index].data = base[segment_tree[index].start];
segment_tree[index].mark = 0;
return;
}
// 递归建左子树和右子树
int mid = (start + end) >> 1;
build(start, mid, (index << 1) + 1);
build(mid, end, (index << 1) + 2);
// 根据左儿子右儿子更新当前结点的值
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
segment_tree[index].mark = 0;
}
区间查询
区间查询,即查询给定区间[a, b)的最小值。
- 查询策略: 若当前结点为Node

- 例: 在上方树中,查询区间[1, 5)最小值

- 黄色:需要细化查询, 返回左右儿子返回值的最小值。
- 绿色:完全被[1,5)覆盖,直接返回当前data。
- 红色:[1,5)之外的区间,不应该影响最终结果,返回一个极大值。
- 代码:根据示意图,很容易写出代码:
int query(int a, int b, int index)
{
/*
[a, b): 查询区间
index: 当前查询节点在segment_tree数组中的下标
返回: [a,b)和[Node.start, Node.end)交集的最小值。 其中Node = segment_tree[index]
*/
// 情况一:完全覆盖
if(a <= segment_tree[index].start && segment_tree[index].end <= b)
{
return segment_tree[index].data;
}
// 情况二:交集为空
else if(a >= segment_tree[index].end || b <= segment_tree[index].start)
{
return INF;
}
// 情况三:细化查询
int v1 = query(a, b, (index << 1) + 1);
int v2 = query(a, b, (index << 1) + 2);
return min(v1, v2);
}
单点改变
现在我们要改变线段树叶子节点的某一个值。比如将第1个值1改为3。很明显,我们需要先定位,更改,再将影响向上传播。示意图如下:

- 代码:根据示意图,很容易写出代码:
void update_one(int p, int x, int index)
{
/*
p: 要更改的元素位置
x: 将位置p的元素更改为x
index: 当前结点在segment_tree数组中的下标
*/
// 定位成功
if(segment_tree[index].start == p && segment_tree[index].start == segment_tree[index].end-1)
{
segment_tree[index].data = x;
return;
}
int mid = (segment_tree[index].start + segment_tree[index].end) >> 1;
// 需要更改的位置在右子树
if(p >= mid)
{
update_one(p, x, (index << 1) + 2);
}
// 需要更改的位置在左子树
else
{
update_one(p, x, (index << 1) + 1);
}
// 根据左右儿子更新当前结点值
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
}
区间改变
这里我们模拟将整个区间[a, b)整体加上一个数字c。 可用的策略是对区间[a, b)的每个数都进行一个单点更新,但是最终会导致O(NlogN)的时间复杂度。为了降低复杂度,我们引入延时更新策略:
- (1)完全包含: 区间[a,b)完全包含[Node.start, Node,end),那我们先将该更新记录到Node的mark中,并只更新Node的data, 同时更新其祖先的值。
- (2)毫不相交:不做处理
- (3)需要细化: 直到细化区间更新或者细化区间查询操作到来, 我们将父节点记录的更新信息传递给子节点。
现在我们逐一解释该策略:
- 对(1): 如图,我们对区间[1,3)的每个数都增加3, 因此我们将代表区间[1,3)的节点的mark值记为3,并更新其data,更新后,我们便不再继续向下更新,而是直接返回并更新其祖先的值。
- 对(3): 遇到细化区间更新,比如在更区间[1,3)基础上,我们希望再将区间[0,2)的值增加2。因为[0,2)和区间[1,3)有交集也有不同。因此我们先将[1,3)的更新信息传递到子节点。
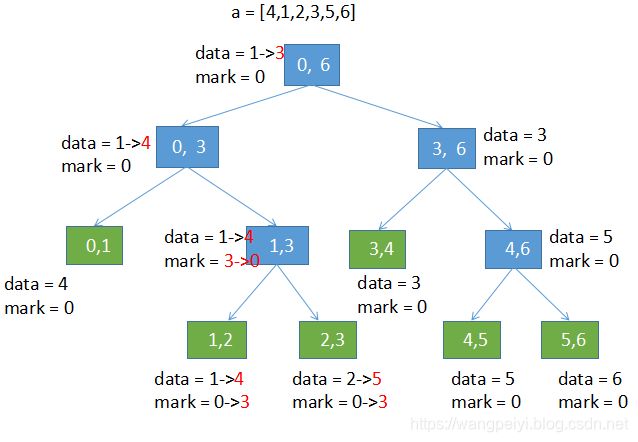
然后再执行对[0,2)加2的更新操作

最后完成更新。 - 代码:根据图示,我们很容易写出代码
void push_down(int index)
{
/*
将segment_tree[index]的段更新信息传递到子节点,并清除掉自己的标记
*/
int mark = segment_tree[index].mark;
if(mark != 0)
{
segment_tree[(index << 1) + 1].mark += mark;
segment_tree[(index << 1) + 2].mark += mark;
segment_tree[(index << 1) + 1].data += mark;
segment_tree[(index << 1) + 2].data += mark;
}
segment_tree[index].mark = 0;
}
void update_seg(int a, int b, int add, int index)
{
/*
[a, b): 需要更新的区间
add: 区间[a, b)需要增加的数
index: 当前结点在segment_tree中的下标
*/
// 情况一: 完全包含, 只维护该节点与其祖先
if(a <= segment_tree[index].start && segment_tree[index].end <= b)
{
segment_tree[index].data += add;
segment_tree[index].mark += add;
return;
}
// 情况二:完全不相交,跳过
else if(a >= segment_tree[index].end || b <= segment_tree[index].start)
{
return;
}
// 情况三:需要细化更新
push_down(index); // 将当前结点保存的更新信息推向儿子节点
update_seg(a, b, add, (index << 1) + 1);
update_seg(a, b, add, (index << 1) + 2);
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
}
- 对(3): 遇到细化区间查询是指在如下状态时:
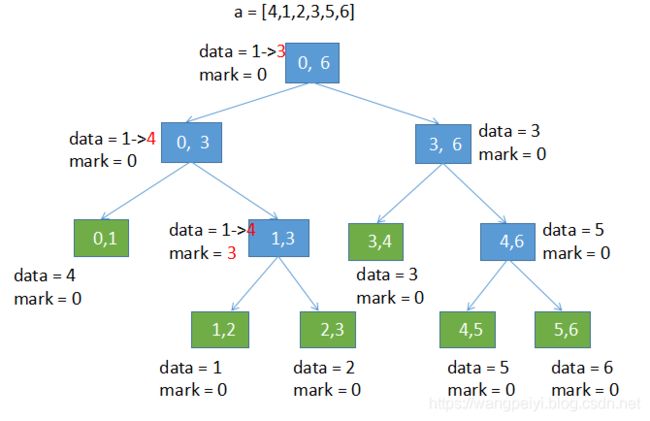
我们希望查询[0,2)的最小值。这时我们需要将[1,3)区间的节点的更新信息先传递下去。

这样,我们才能查询到[1,2)节点的最新信息。
- 代码:我们只需要对原始代码稍作修改
int query(int a, int b, int index)
{
/*
[a, b): 查询区间
index: 当前查询节点在segment_tree数组中的下标
返回: [a,b)和[Node.start, Node.end)交集的最小值。 其中Node = segment_tree[index]
*/
// 情况一:完全覆盖
if(a <= segment_tree[index].start && segment_tree[index].end <= b)
{
return segment_tree[index].data;
}
// 情况二:交集为空
else if(a >= segment_tree[index].end || b <= segment_tree[index].start)
{
return INF;
}
// 情况三:细化查询
// --------------------加入此行---------------------------------
push_down(index);
// -----------------------------------------------------------
int v1 = query(a, b, (index << 1) + 1);
int v2 = query(a, b, (index << 1) + 2);
return min(v1, v2);
}
例题
- Balanced Lineup(维护区间最大最小值,区间查询)
- Minimizing maximizer(动态规划+维护区间最小值,单点更新)
- A Simple Problem with Integers(维护区间和,区间整体更新查询)
- Crane(维护区间向量和, 区间整体更新查询)
博客示例完整代码
#include
using namespace std;
const int MAXN = 100000;
const int INF = 100000+5;
struct Node
{
int start;
int end;
int data;
int mark;
}segment_tree[MAXN*4];
int base[MAXN];
void build(int start, int end, int index)
{
/*
[start, end): 目前建立节点负责区间负责区间
index: 目前建立结点在segment_tree数组中的下标
使用方式: 针对数据: int base[6] = {4,1,2,3,5,6};
调用build(0, 6, 0)完成建树
*/
// 赋值区间
segment_tree[index].start = start ;
segment_tree[index].end = end;
// 如果已经到了叶子节点
if(segment_tree[index].start == segment_tree[index].end - 1)
{
segment_tree[index].data = base[segment_tree[index].start];
segment_tree[index].mark = 0;
return;
}
// 递归建左子树和右子树
int mid = (start + end) >> 1;
build(start, mid, (index << 1) + 1);
build(mid, end, (index << 1) + 2);
// 根据左儿子右儿子更新当前结点的值
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
segment_tree[index].mark = 0;
}
void update_one(int p, int x, int index)
{
/*
p: 要更改的元素位置
x: 将位置p的元素更改为x
index: 当前结点在segment_tree数组中的下标
*/
// 定位成功
if(segment_tree[index].start == p && segment_tree[index].start == segment_tree[index].end-1)
{
segment_tree[index].data = x;
return;
}
int mid = (segment_tree[index].start + segment_tree[index].end) >> 1;
// 需要更改的位置在右子树
if(p >= mid)
{
update_one(p, x, (index << 1) + 2);
}
// 需要更改的位置在左子树
else
{
update_one(p, x, (index << 1) + 1);
}
// 根据左右儿子更新当前结点值
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
}
void push_down(int index)
{
/*
将segment_tree[index]的段更新信息传递到子节点,并清除掉自己的标记
*/
int mark = segment_tree[index].mark;
if(mark != 0)
{
segment_tree[(index << 1) + 1].mark += mark;
segment_tree[(index << 1) + 2].mark += mark;
segment_tree[(index << 1) + 1].data += mark;
segment_tree[(index << 1) + 2].data += mark;
}
segment_tree[index].mark = 0;
}
void update_seg(int a, int b, int add, int index)
{
/*
[a, b): 需要更新的区间
add: 区间[a, b)需要增加的数
index: 当前结点在segment_tree中的下标
*/
// 情况一: 完全包含, 只维护该节点与其祖先
if(a <= segment_tree[index].start && segment_tree[index].end <= b)
{
segment_tree[index].data += add;
segment_tree[index].mark += add;
return;
}
// 情况二:完全不相交,跳过
else if(a >= segment_tree[index].end || b <= segment_tree[index].start)
{
return;
}
// 情况三:需要细化更新
push_down(index); // 将当前结点保存的更新信息推向儿子节点
update_seg(a, b, add, (index << 1) + 1);
update_seg(a, b, add, (index << 1) + 2);
segment_tree[index].data = min(segment_tree[(index << 1) + 1].data, segment_tree[(index << 1) + 2].data);
}
int query(int a, int b, int index)
{
/*
[a, b): 查询区间
index: 当前查询节点在segment_tree数组中的下标
返回: [a,b)和[Node.start, Node.end)交集的最小值。 其中Node = segment_tree[index]
*/
// 情况一:完全覆盖
if(a <= segment_tree[index].start && segment_tree[index].end <= b)
{
return segment_tree[index].data;
}
// 情况二:交集为空
else if(a >= segment_tree[index].end || b <= segment_tree[index].start)
{
return INF;
}
// 情况三:细化查询
push_down(index);
int v1 = query(a, b, (index << 1) + 1);
int v2 = query(a, b, (index << 1) + 2);
return min(v1, v2);
}
int main()
{
int n;
cout << "输入数组长度:" << endl;
cin >> n;
cout << "输入" << n << "个整数(空格隔开):" << endl;
for(int i=0; i> base[i];
}
cout << "正在建树.." << endl;
build(0, n, 0);
cout << "建树完成.." << endl;
int op;
int a, b;
int add;
int pos;
int x;
do{
cout << "输入操作:" << endl;
cout << "0: 退出\n1: 查询区间最小值\n2: 单点改变某个值\n3: 区间整体增加某个值\n";
cin >> op;
if(op == 1)
{
cout << "输入区间起始位置a,b(区间为:[a, b)):" << endl;
cin >> a >> b;
cout << "区间[" << a << "," << b << ")最小值为:";
cout << query(a, b, 0) << endl;
}
else if(op == 2)
{
cout << "输入改变值的位置:";
cin >> pos;
cout << "输入改变后的值:";
cin >> x;
update_one(pos, x, 0);
cout << "单点改变成功" << endl;
}
else if(op == 3)
{
cout << "输入区间其实位置a,b(区间为:[a, b))" << endl;
cin >> a >> b;
cout << "要增加的值:" << endl;
cin >> add;
update_seg(a, b, add, 0);
cout << "区间更改成功" << endl;
}
cout << endl << endl;
}while(op != 0);
return 0;
}