【python】sort函数的时间+空间复杂度(包括py内置.sort())
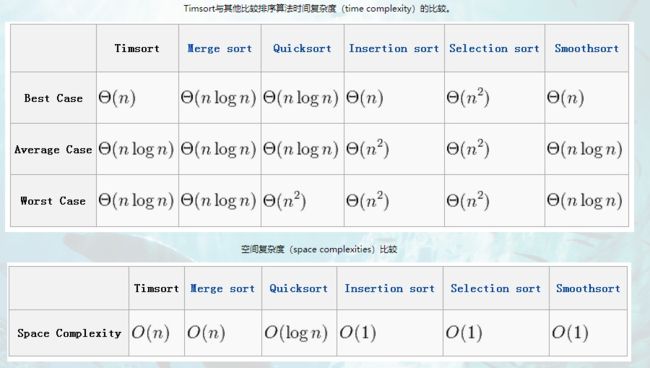
python有个内置的nums.sort()排序函数,其内部实现机制为:Timesort
最坏时间复杂度为:O(n log n)
空间复杂度为:O(n)
顺便整理一下其他的各种排序算法:
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 排序方式 | 稳定性 |
|---|---|---|---|---|---|---|
| 插入排序 | O(n²) | O(n) | O(n²) | O(1) | In-place | 稳定 |
| 冒泡排序 | O(n²) | O(n) | O(n²) | O(1) | In-place | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | In-place | 不稳定 |
| 快速排序 | O(n log n) | O(n log n) | O(n²) | O(log n) | In-place | 不稳定 |
| 希尔排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | In-place | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Out-place | 稳定 |
直接插入排序:
def insert_sort(array):
for i in range(len(array)):
for j in range(i):
if array[i] < array[j]:
array.insert(j, array.pop(i))
break
return array
希尔排序:
def shell_sort(array):
gap = len(array)
while gap > 1:
gap = gap // 2
for i in range(gap, len(array)):
for j in range(i % gap, i, gap):
if array[i] < array[j]:
array[i], array[j] = array[j], array[i]
return array
选择排序:
def select_sort(array):
for i in range(len(array)):
x = i # min index
for j in range(i, len(array)):
if array[j] < array[x]:
x = j
array[i], array[x] = array[x], array[i]
return array
堆排序:
def heap_sort(nums):
# 调整堆
# 迭代写法
def adjust_heap(nums, startpos, endpos):
newitem = nums[startpos]
pos = startpos
childpos = pos * 2 + 1
while childpos < endpos:
rightpos = childpos + 1
if rightpos < endpos and nums[rightpos] >= nums[childpos]:
childpos = rightpos
if newitem < nums[childpos]:
nums[pos] = nums[childpos]
pos = childpos
childpos = pos * 2 + 1
else:
break
nums[pos] = newitem
# 递归写法
def adjust_heap(nums, startpos, endpos):
pos = startpos
chilidpos = pos * 2 + 1
if chilidpos < endpos:
rightpos = chilidpos + 1
if rightpos < endpos and nums[rightpos] > nums[chilidpos]:
chilidpos = rightpos
if nums[chilidpos] > nums[pos]:
nums[pos], nums[chilidpos] = nums[chilidpos], nums[pos]
adjust_heap(nums, pos, endpos)
def heap_sort(array):
def heap_adjust(parent):
child = 2 * parent + 1 # left child
while child < len(heap):
if child + 1 < len(heap):
if heap[child + 1] > heap[child]:
child += 1 # right child
if heap[parent] >= heap[child]:
break
heap[parent], heap[child] = \
heap[child], heap[parent]
parent, child = child, 2 * child + 1
heap, array = array.copy(), []
for i in range(len(heap) // 2, -1, -1):
heap_adjust(i)
while len(heap) != 0:
heap[0], heap[-1] = heap[-1], heap[0]
array.insert(0, heap.pop())
heap_adjust(0)
return array
冒泡排序:
def bubble_sort(array):
for i in range(len(array)):
for j in range(i, len(array)):
if array[i] > array[j]:
array[i], array[j] = array[j], array[i]
return array
快速排序:
def Quick_sort(num_list):
'''
快速排序,时间复杂度:O(nlog₂n),空间复杂度:O(nlog₂n),不是稳定排序
'''
if len(num_list)<2:
return num_list
left_list = [] #存放比基准结点小的元素
right_list = [] #存放比基准元素大的元素
base_node = num_list.pop(0) #在这里采用pop()方法的原因就是需要移除这个基准结点,并且赋值给base_node这个变量
#在这里不能使用del()方法,因为删除之后无法再赋值给其他变量使用,导致最终数据缺失
#快排每轮可以确定一个元素的位置,之后递归地对两边的元素进行排序
for one_num in num_list:
if one_num < base_node:
left_list.append(one_num)
else:
right_list.append(one_num)
return Quick_sort(left_list) + [base_node] + Quick_sort(right_list)
归并排序:
def merge_sort(nums):
if len(nums) <= 1:
return nums
mid = len(nums) // 2
# 分
left = merge_sort(nums[:mid])
right = merge_sort(nums[mid:])
# 合并
return merge(left, right)
def merge(left, right):
res = []
i = 0
j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
res.append(left[i])
i += 1
else:
res.append(right[j])
j += 1
res += left[i:]
res += right[j:]
return res
基数排序:
def radix_sort(array):
bucket, digit = [[]], 0
while len(bucket[0]) != len(array):
bucket = [[], [], [], [], [], [], [], [], [], []]
for i in range(len(array)):
num = (array[i] // 10 ** digit) % 10
bucket[num].append(array[i])
array.clear()
for i in range(len(bucket)):
array += bucket[i]
digit += 1
return array
参考大佬整理内容,附链接:
【算法】八大排序以及时间空间复杂度分析以及用Python实现 - 雪原那么远 - 博客园 (cnblogs.com)