2011NOIP普及组初赛真题解析

---

前言

11年的题目选择题考得比较广，还好考得比较基础难度并不高，比较烦人的是那种 计算机基础知识题和常识题，对于普通中学生来说计算机基础知识这块是比较薄弱的，只能 多积累。还考到了比较多的 进制、 计算机单位之类的计算类题目，虽然不难但计算的时候要细心，不然容易出错。

填空题考了排列组合和dp，排列组合如果掌握了基本模型的话还是不算太难。dp那道题目难度还是很大的，如果没有做过编辑距离那道题临阵磨枪的话几乎是不可能做出来的。要暴力枚举出来也很容易出错，不是很容易的事情，要是在考场上遇到，对普通人来说，乱填一个答案是更明智的选择。

代码阅读还是很简单的，3道题目都是模拟，样例也很小，要拿下不是什么难事。最后一道递归直接做比较麻烦，本来递归的求解过程就比较复杂还包含了重叠子问题，把它倒过来当做递推来做就很快了。

代码填空第1题是简单的模拟，变量命名很规范，而且很多要填的空都有很明显的对比、对称关系。如果是学过高精度、二分法，基础还可以的同学，第2题还是很简单的，好多空的思路都是很像的，毕竟高精度的处理都大同小异。

具体的考点如下图：

视频链接：2011NOIP普及组初赛真题解析

选择题

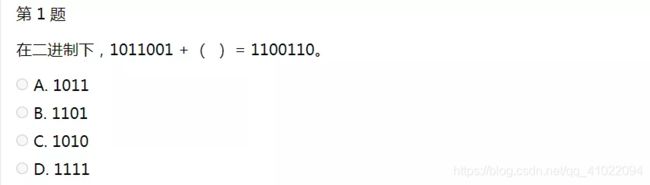★考点：
二进制运算
解析：
二进制运算和十进制运算一样，只是把运算法则变成了逢二进一、借一当二。
相： 1100110
减： 1011001
结果：0001101
故选B

★考点：
字符
解析：
字符中数字的ASCII码是连续的，'0’的ASCII码是48，'9’的ASCII码=48+9，故选B



★考点：
计算机单位
解析：
8G=(8*1024M)/2M≈4000，故选C



★考点：
计算机基础知识
解析：
选C，没什么好说的，靠积累


★考点：
图论
解析：
可以先画出当顶点数为2、3、4的完全无向图，观察边的数量，看看能否看出规律。

  根据完全无向图的概念，7个顶点的每一个顶点都要和其它的6个顶点要有边。顶点1要和剩下6个顶点(2、3、4、5、6、7)有边，边数+6；顶点2也要和剩下5个顶点(3,、4、5、6、7)有边，边数+5；顶点3要和剩下的4个顶点(4、5、6、7)有边，边数+4…，以此类推，7个顶点的完全无向图边数为1+2+3+4+5+6=21。故选B



★考点：
计算机基础知识
解析：
选C，多积累

★考点：
二叉树
解析：
深度最少就是要树尽可能的矮，也就是要完全二叉树，由图可知

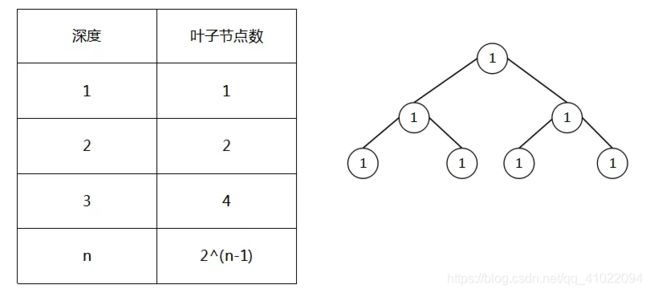
当完全二叉树深度为n时，叶子节点总数为2^(n-1) ，2^(12-1)=2047>=2011，故选C



★考点：
插入排序
解析：
  操场上是已经排好序的队伍，刚来到操场的同学从后往前找到合适的位置插入进去，很明显是插入排序，故选B



★考点：
进制转换
解析：
  4位二进制可以用一位十六进制来表示，所以100位的二进制可以用100/4=25位的十六进制表示，故选C



★考点：
常识题
解析：
选C，我不明白这和编程有啥关系



★考点：
bfs
解析：
bfs访问的节点顺序需要保证先进先出的顺序，故选B



★考点：
空间复杂度
解析：
选A，考空间复杂度的概念，就算没可以去背，也可以用排除法选出来



★考点：
链表
解析：
  个人认为题目有点歧义，把最快情况下改成最坏情况下会更恰当，链表访问元素只能一个一个往下找，故选C



★考点：
常识题
解析：
  都不明白它想考啥，把考点归类为常识题，看生物特征识别的概念，辨别两样不用的东西是用某些特征、属性去辨别的。写过一点程序都知道，密码验证都是把直接把验证的密码和正确密码比较是否相同，而不是对比特征、属性，故选C



★考点：
哈夫曼算法
解析：
按照题目要求构造哈夫曼树：
1、从所有的次数集合里挑选两个最小的权值，作为左右子树，将它们合并后的权值作为左右子树的根节点；
2、删除那两个最小的权值，将根节点的权值加入到次数集合中；
3、重复1、2步骤，直到只剩下1个权值，构建好的树即是哈夫曼树；

由图可知"也"字的编码长度是3，故选D



★考点：
计算机基础知识
解析：
  python、c++、java之类的都是高级语言，和人打交道比较多，人比较容易看得懂，封装程度高，速度比较慢。汇编语言是低级语言，和计算机硬件打交道比较多，没那么容易看懂，封装程度低，比较接近机器所以运算速度快。说白了高级语言向人靠近接近人类的思维方式，低级语言向机器靠近和，但低级语言并不低级，也是非常重要的语言，大学还要专门开课去学习。故选D



★考点：
dfs回溯
解析：
  找到一个方向一条路走到黑，走到无路可走就退回来尝试其它的选择，这是dfs回溯的思想，故选A



★考点：
计算机基础知识
解析：
选A，记住就会，没记住就碰运气，记吧



★考点：
图论
解析：
把四个选项代进去，检查5个点是否连通，选A



★考点：
计算机基础知识
解析：
  冯·诺依曼理论的要点是：数字计算机的数制采用二进制；计算机应该按照程序顺序执行。故选C

填空题

★考点：
排列组合
解析：
  有效的序列号可以有0、2、4、6、8个位置是1，计算每一种情况的方案数，把它们加起来就是答案。相当于是在8个位置上挑选0、2、4、6、8个位置，挑选的位置如果改变顺序不影响答案，所以是组合问题。答案为：C（8,0）+C（8，2）+C（8，4）+C（8,6）+C（8,8）=1+28+70+28+1=128，故填128



★考点：
区间dp
解析：
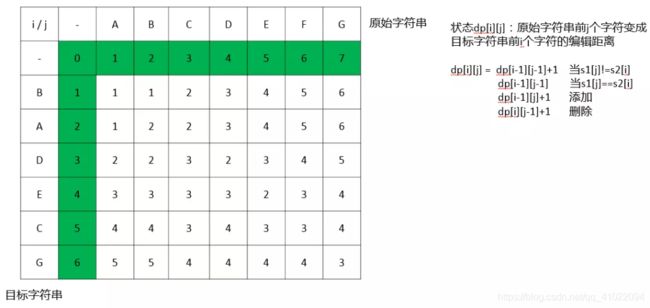
编辑距离，经典dp问题，"ABCDFEFG"为原始串s，"BADECG"为目标串t。
状态划分：先找到重叠子问题，原始串前i个位置到目标串前j个位置的编辑距离就是重叠子问题，建立一个二维的数组，dp[i][j]表示原始串前i个位置到目标串前j个位置的编辑距离。

状态推导：考虑问题的最后一步，编辑问题的最后一步是目标串的第j个字符怎么来的。
  题意已知有删除、插入、修改三种操作，如果最后一步操作是删除，上一次的状态是dp[i][j-1]，状态推导为dp[i][j]=dp[i][j-1]+1，+1是要算上最后一步；如果最后一步是插入，上一次的状态是dp[i-1][j]，状态推导为dp[i][j]=dp[i-1][j]+1。

  如果最后一步是替换，分两种情况，当原始串的第i个字符和目标串第j个字符不相等时，是正常的替换，上一次的状态是dp[i-1][j-1]，状态推导为dp[i][j]=dp[i-1][j-1]+1。当原始串的第i个字符和目标串第j个字符相等时，相当于最后一次替换这个操作不用进行，上一次的状态是dp[i-1][j-1]，状态推导为dp[i][j]=dp[i-1][j-1]。

小结一下，状态dp[i][j]的推导有下面4种情况，取最小值。

• dp[i-1][j]+1
• dp[i][j-1]+1
• dp[i-1][j-1]+1，s[i]!=t[j]
• dp[i-1][j-1]+1，s[i]==t[j]

  样例具体推导如下图所示，"-"相当于是空字符串，原谅色的状态是边界。原字符串到变成空字符串每次只有删除操作，编辑距离为原字符串的长度，空字符串变成目标字符串每次只有插入操作，编辑距离为目标字符串的长度。

代码阅读

第23题
阅读程序写结果
输入：10 20

#include
using namespace std;

int main()
{
    int i,n,m,ans;
    cin>>n>>m;
    i=n;
    ans=0;
    while(i<=m){
       ans+=i;
       i++;
    }
    cout<<ans<<endl;
    return 0;
}

★考点：
模拟
解析：
  i初始化值为n，在while循环里，i每次自增1,直到m为止，ans每次加上i，ans的值为10+11+12+…+19+20=165，故输出为165


第24题
阅读程序写结果
输入：CCF-NOIP-2011

#include
#include
using namespace std;

int main()
{
    string map= "2223334445556667778889999";
    string tel;
    int i;
    cin>>tel;
    for(i=0;i<tel.length();i++)
       if((tel[i]>='0') && (tel[i]<='9') )
           cout<<tel[i];
       else if( (tel[i]>='A') && (tel[i]<='Z'))
           cout<<map[tel[i]-'A'];
    cout<<endl;
    return 0;
}

★考点：
模拟、字符串
解析：
  读入字符串后遍历字符串，如果字符是数字直接打印，如果是大写字母，先减去’A’得到这是第几个大写字母，然后打印map中对应的数字，故输出为22366472011


第25题
阅读程序写结果
输入：
11
4 5 6 6 4 3 3 2 3 2 1

#include
#include
using namespace std;

const int SIZE = 100;

int main()
{
    int n,i,sum,x,a[SIZE];
    
    cin>>n;
    memset(a,0,sizeof(a));
    
    for(i=1;i<=n;i++){
        cin>>x;
        a[x]++;
    }
    i=0;
    sum=0;
    while(sum<(n/2+1)){
        i++;
        sum+=a[i];
    }
    cout<<i<<endl;
    return 0;
}

★考点：
模拟、计数排序
解析：
输入n个数字，在a数组的每个位置上+1，a数组相当于是记录每个数字出现的次数。

  在while循环里，i初始值为0，每次自增，sum初始值为0，每次加上a[i]（即数字i出现的次数），即sum记录数字0到数字i的出现次数，当出现次数大于等于一半退出循环，最后打印i。故输出为3


第26题
阅读程序写结果
输入：7 4

#include
using namespace std;

int solve(int n,int m)
{
    int i,sum;
    if(m==1) return 1;
    sum=0;
    for(i=1;i<n;i++)
       sum+= solve(i,m-1);
    return sum;
}

int main()
{
    int n,m;
    cin>>n>>m;
    cout<<solve(n,m)<<endl;
    return 0;
}

★考点：
递归、递推
解析：
  考的是递归，如果正常按照流程去求解，部分过程如下图，递归的求解过程很麻烦，而且有大量的重叠子问题。

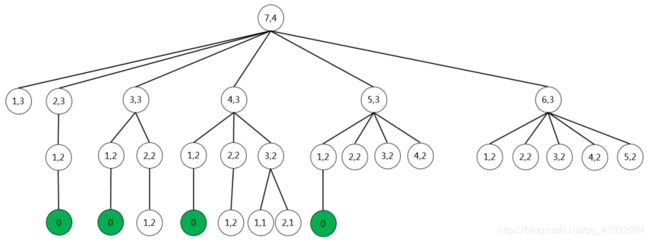
  可以把它倒过来思考，当做是递推来做，求解过程如下，由递归函数可以知道当m==1返回1，当n ==1返回0，当做是边界，图中标成了原谅色。

故输出为20

代码填空

第 27 题 完善程序 （子矩阵）给输入一个n1m1的矩阵a，和n2m2的矩阵b，问a中是否存在子矩阵和b相等。若存在，输出所有子矩阵左上角的坐标：若不存在输出“There is no answer”。

#include
using namespace std;

const int SIZE = 50;

int n1,m1,n2,m2,a[SIZE][SIZE],b[SIZE][SIZE];


int main()
{
    int i,j,k1,k2;
    bool good ,haveAns;

    cin>>n1>>m1;
    for(i=1;i<=n1;i++)
       for(j=1;j<=m1;j++)
          cin>>a[i][j];
          
    cin>>n2>>m2;
    for(i=1;i<=n2;i++)
       for(j=1;j<=m2;j++)
           [ ① ];
          
    haveAns=false;
    for(i=1;i<=n1-n2+1;i++)
       for(j=1;j<= [ ② ];j++){
            [ ③ ];
           for(k1=1;k1<=n2;k1++)
               for(k2=1;k2<=[ ④ ] ;k2++){
                  if(a[i+k1-1][j+k2-1]!=b[k1][k2])
                     good=false;
               }
          if(good){
             cout<<i<<' '<<j<<endl;
             [ ⑤ ];
          }
       }
    if(!haveAns)
       cout<<"There is no answer"<<endl;

    return 0;
}

★考点：
模拟
解析：
  题目已经告诉我们程序的功能了，先简单略读一下程序，明白代码的大概含义，写上一些注释，然后再去填空。

#include
using namespace std;
const int SIZE = 50;
int n1,m1,n2,m2,a[SIZE][SIZE],b[SIZE][SIZE];
int main()
{
    int i,j,k1,k2;
    bool good ,haveAns;
  //输入矩阵a 
    cin>>n1>>m1;
    for(i=1;i<=n1;i++)
       for(j=1;j<=m1;j++)
          cin>>a[i][j];
    //输入矩阵b      
    cin>>n2>>m2;
    for(i=1;i<=n2;i++)
       for(j=1;j<=m2;j++)
           [   ①     ];
    //判断a是否存在子矩阵b      
    haveAns=false;//是否存在子矩阵b的标记 
    for(i=1;i<=n1-n2+1;i++)//枚举行，从1到n1-n2+1，很明显这是枚举子矩阵的行 
       for(j=1;j<= [    ②     ];j++){//这里应该是枚举子矩阵的列 
            [   ③    ];
           //判断子矩阵是否和b相同 
       for(k1=1;k1<=n2;k1++)
               for(k2=1;k2<=[    ④    ] ;k2++){
                  if(a[i+k1-1][j+k2-1]!=b[k1][k2])//如果子矩阵的数字和b矩阵上的数字对不上 
                     good=false;//由此可见，good是判断子矩阵是否和b相同的标记 
               }
          if(good){//如果good为true，说明目前的子矩阵和b矩阵相同，打左上角的下标 
             cout<<i<<' '<<j<<endl;
             [       ⑤      ];
          }
       }
    //如果遍历所有的子矩阵都没有找到和b矩阵相同的，说明不存在，可知haveAns变量是用来判断有无矩阵b额标记 
  if(!haveAns)
       cout<<"There is no answer"<<endl;

    return 0;
}

1、由14行注释可知，这两个嵌套for循环的作用是输入矩阵b，故第1个空为cin>>b[i][j]。

2、22行的for循环是用来子矩阵的列，故第2个空为m1-m2+1。

3、由28行和33行可知good是判断子矩阵是否和b相同的标记 ，但在判断子矩阵和b是否相同前没有对good进行初始化，故第3个空为good=true。

4、由24行的注释可知嵌套fo循环k1、k2是用来枚举矩阵b，判断是否和子矩阵相同的，故第4个空为m2。

5、由36行的代码可知，变量haveAns是用来判断是否存在矩阵b的标记，如果发现了和矩阵b相同的子矩阵，应该要更新haveAns这个标记，故第5个空为haveAns=true。


第 28 题
完善程序
(大整数开方) 输入一个正整数n（1≤n≤10^100），试用二分法计算它的平方根的整数部分。

#include
#include
using namespace std;

const int SIZE=200;
struct hugeint{
    int len,num[SIZE];
};
//其中len表示大整数的位数；num[1]表示个位，num[2]表示十位，以此类推

hugeint times(hugeint a,hugeint b)
// 计算大整数a和b的乘积
{
    int i,j;
    hugeint ans;
    memset(ans.num,0,sizeof(ans.num));
    for(i=1;i<=a.len;i++)
       for(j=1;j<=b.len;j++)
            [ ① ] +=a.num[i]*b.num[j];
    for(i=1;i<=a.len+b.len;i++){
        ans.num[i+1]+=ans.num[i]/10;
        [ ② ];
    }
    if(ans.num[a.len+b.len]>0)
        ans.len=a.len+b.len;
    else
        ans.len=a.len+b.len-1;
    return ans;
}

hugeint add(hugeint a,hugeint b)
//计算大整数a和b 的和
{
    int i;
    hugeint ans;
    memset(ans.num,0,sizeof(ans.num));
    if(a.len>b.len)
        ans.len=a.len;
    else
        ans.len=b.len;
    for(i=1;i<=ans.len;i++){
        ans.num[i]+= [ ③ ] ;
        ans.num[i+1]+= ans.num[i]/10;
        ans.num[i]%=10;
    }
    if(ans.num[ans.len+1]>0)
        ans.len++;
    return ans;
}

hugeint average(hugeint a,hugeint b)
//计算大整数a和b的平均数的整数部分
{
    int i;
    hugeint ans;
    ans=add(a,b);
    for(i=ans.len;i>=2;i--){
        ans.num[i-1]+=([ ④ ])*10;

        ans.num[i]/=2;
    }
    ans.num[1]/=2;
    if(ans.num[ans.len]==0)
        ans.len--;
    return ans;
}

hugeint plustwo(hugeint a)
// 计算大整数a加2之后的结果
{
    int i;
    hugeint ans;
    ans=a;
    ans.num[1]+=2;
    i=1;
    while( (i<=ans.len)&&(ans.num[i]>=10) ){
        ans.num[i+1]+=ans.num[i]/10;
        ans.num[i]%=10;
        i++;
    }
    if(ans.num[ans.len+1]>0)
        [ ⑤ ];
    return ans;
}

bool over(hugeint a,hugeint b)
// 若大整数a>b则返回true，否则返回false
{
    int i;
    if([ ⑥ ])
        return false;
    if( a.len>b.len )
        return true;
    for(i=a.len;i>=1;i--){
        if(a.num[i]<b.num[i])
           return false;
        if(a.num[i]>b.num[i])
           return true;
    }
    return false;
}

int main()
{
    string s;
    int i;
    hugeint target,left,middle,right;
    cin>>s;
    memset(target.num,0,sizeof(target.num));
    target.len=s.length();
    for(i=1;i<=target.len;i++)
        target.num[i]=s[target.len-i]-[ ⑦ ];
    memset(left.num,0,sizeof(left.num));
    left.len=1;
    left.num[1]=1;
    right=target;
    do{
        middle=average(left,right);
        if(over([ ⑧ ]))
            right=middle;
        else
            left=middle;
    }while(!over(plustwo(left),right) );
    for(i=left.len;i>=1;i--)
       cout<<left.num[i];
    return 0;
}

★考点：
二分法、高精度
解析：
  二分法求高精度大数的平方根，注释已经写得比较明白了，如果知道二分法和高精度的话，是很容易做出来的，基本上是送分，美滋滋。

1、times(a,b)求a和b乘积的函数，上面的嵌套for循环是拿来求a乘b的结果保存到ans对应的位置，故第1个空为ans.num[i+j-1]。如果不放心，可以拿几个小样例 测试一下，下图为数字345*21的运算过程，黄色的表示参与运算的数字，绿色的表示更新过的结果

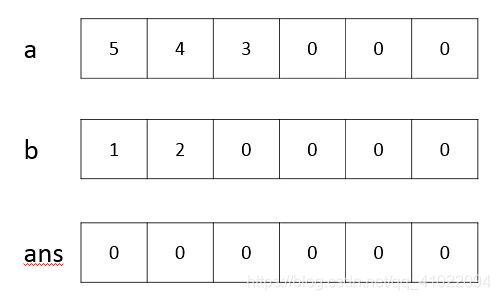
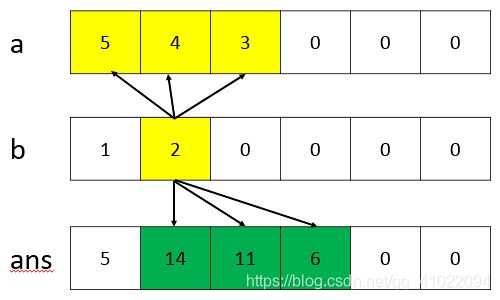
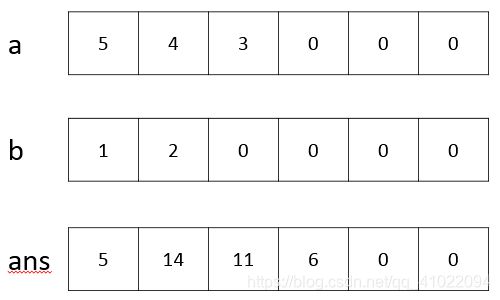
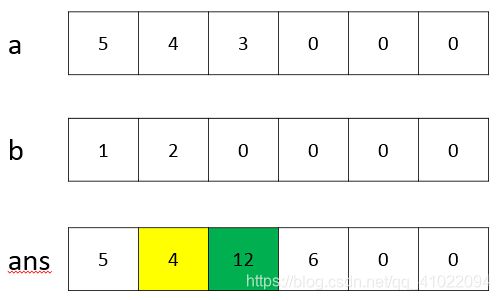
2、times(a,b)下面的循环是来处理进位的，ans.num[i+1]+=ans.num[i]/10；这行代码是将第i个位置的进位加到第i+1位，接下来还要取数字的个位保存到第i个位置，故第2个空为ans.num[i]%=10。下图为数字345*21的运算后结果的处理进位过程，黄色的当前要处理的数字，绿色的表示更新过的进位

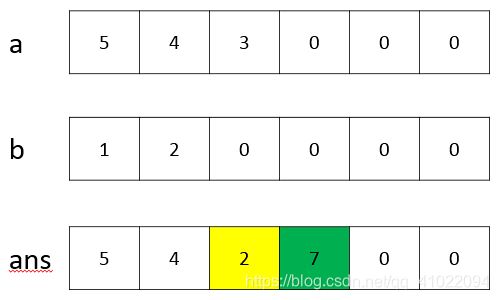
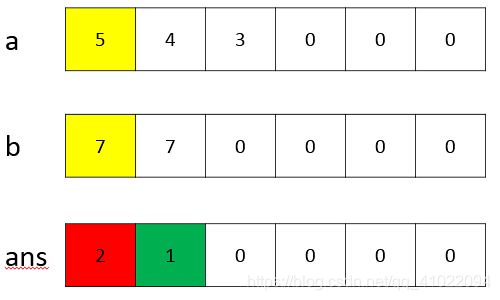
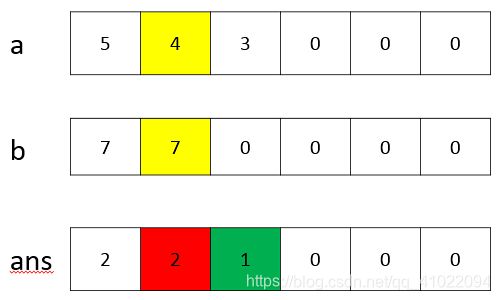
3、第3个空后面的两行代码是对ans.num[i]上的数字进行处理，所以在这应该已经把a、b的和加好了，故第3个空为a.num[i]+b.num[i]。下图为数字345+77的运算过程，黄色的当前要参与运算的数字，红色的表示运算后存放的结果，绿色的表示要新过的进位

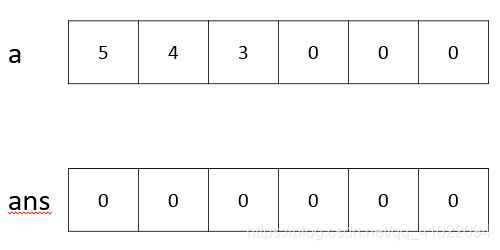
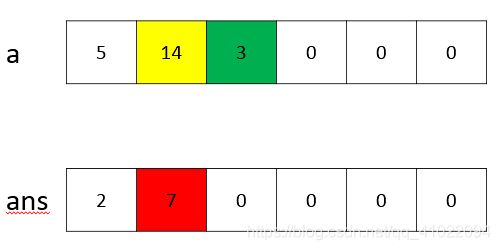
4、average(a,b)是计算大整数a和b的平均数的整数部分，计算方法是求a和b的和，把和从高位到低位除以2，把除不尽余下的数乘以10加到下一位，第4个空的代码是要除不尽余下的数放到下一位，故第4个空为ans.num[i]%2。下图为数字345除2的运算过程，黄色的当前要参与运算的数字，红色的表示运算后存放的结果，绿色的表示要新的数字

5、plustwo(a)是计算a+2，在a的基础上+2之后，进行了进位处理，如果最高位的上一位是大于0的话，说明有进位溢出了，需要把ans的长度+1，故第5个空填ans.len++

6、over(a,b)判断a>b，哪个数字长就是哪个数字大，如果数字一样长，就把数字从高位往低位比。如果a的高位比b的高位大，说明a>b，反之说明a<=b，故第6个空填a.len

7、读入的s是字符串，我们要放到target中，不仅要倒着放而且要存放数字，所以要把每个字符都转成数字，故第7个空填’0’

8、over(a,b)是用来比较a、b大小的，由附件的二分代码可知，求平方根是通过比较中间值middle²和目标值target的大小。如果middle²>target，说明middle大了，right=middle，否则说明小了，left=middle，故第8个空填times(middle,middle),targe


没有人，想在年少的时候成为一个普通人。感谢你的观看，欢迎点赞、评论，也欢迎关注我的公众号【可乐学算法】，更多noip/csp真题解析在我的公众号上。