【文科生带你读JavaScript数据结构与算法】1. 双向链表与LRU缓存算法原理与实现（上）

前言：最近又开始重学数据结构与算法了（嗯，这么些年来确实重学N遍了，但这次和winter大神《重学前端》里讲的“重学”概念比较接近了，对自己来说应该会有比较明显的学习效果），和优秀的前辈一起交流学习果然能极速提升自己的思维水平和认知格局，比起自己一个人闷头啃书或者刷视频来的高效多了，能遇到一位乐意与自己交流技术的code-mate，绝对是自己成长道路上极其宝贵的财富。在这里首先感谢一下我身边那位科班出身见多识广的C++大佬超哥，从CPU外部三大总线结构到C++多线程与并发控制实践经验再到线程安全性与线程锁的性能权衡，从OSI七层模型的数据链路层、传输层与网络层详解到丢包对TCP和UDP应用层各协议分别的影响再到数据的大小端模式差异都能娓娓道来，给我讲的头头是道，比听德云社相声都得劲儿。如果你也可以和我一样，那么我觉得，这件事情——太酷啦！回家后果断决定趁热打铁，开始写个新的专栏。不过，这个专栏系列并没有严格遵循从哪儿到哪儿的那种逻辑次序，不定期更新，哪天看到哪个然后心血来潮了就先写哪个吧 ​​​​​​​​​​​​​​

---

 打个广告：欢迎关注我的B站主页，本文也同步更新B站专栏文章

【松尾鷹志的个人空间-哔哩哔哩】 https://b23.tv/NsEL2y9​​​​​​​​​​​​​​

福利：首先这里强烈安利一个方便前端同学快速理解数据结构与算法的保姆级人类高质量开源项目，我不允许你不知道：The Algorithms - JavaScript，整个项目中有相当详细的注释、文档、图解，多种实现方式的代码，以及一整套测试场景覆盖齐全的jest自动化测试案例，目前GitHub上的Star数已经达到26.5k+了，还愣着干嘛，快去点起来啊！

OK，回归正题，今天来聊一聊数据结构中的双向链表（doubly linked list），以及一种前端框架中相当常见，且日常工作中也非常实用的优化算法——LRU缓存（Least Recently Used Cache）算法，因为LRU缓存算法是我转行前端早些年接触过印象最深（这里的印象深刻仅仅指的是觉得卧槽好高大上好牛逼但就是啥啥都不懂的那种‍♂️）的一个优化算法，Vue的keep-alive组件缓存机制、用来处理缓存逻辑的知名npm包lru-momoize，还有Redis的过期策略和内存淘汰机制，他们缓存逻辑的核心算法也都是用它来实现的，所以第一篇就先写它好了（对不住了，队列、优先队列二位兄台，只能下次有机会再聊你俩了）。 

Are you ready? Let’s start!

---

目录

双向链表（doubly linked list） 

原理篇

基本概念

基本结构

基本操作方法

增

删

查

改（没这种操作️）

逆向

其他方法 

复杂度

代码篇

双向链表节点构造类DoublyLinkedListNode

​​​​​​​实现方式

双向链表构造类DoublyLinkedList

构造方法

增方法 prepend(value)

增方法 append(value)

删方法 delete(value)

删方法 deleteHead()

删方法 deleteTail()

查方法 find(value)

逆向方法reverse()

其他方法

---

双向链表（doubly linked list） 

原理篇

基本概念

国际惯例，先上一个相对官方的概念。以下概念整理自上述项目的说明文档中：

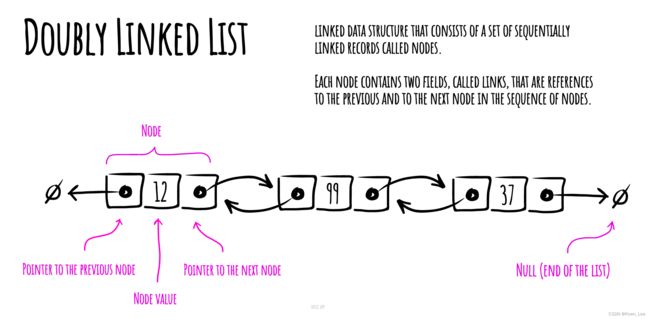
在计算机科学中, 一个 双向链表（doubly linked list 或者我们俗称它为双链表也行），是由一组称为节点的顺序链接记录组成的链接数据结构。每个节点包含两个字段，称为链接，它们是对节点序列中上一个节点和下一个节点的引用。开始节点和结束节点的上一个链接和下一个链接分别指向某种终止节点，通常是前哨节点或null，以方便遍历列表。如果只有一个前哨节点，则列表通过前哨节点循环链接。它可以被概念化为两个由相同数据项组成的单链表，但顺序相反。

没xx说个图，那就先看图吧：

结合这张字迹优雅的示意图（人家原作者画的，字体是真的漂亮，求同款！）来看，上面这段概念的前半段说实话一点也不难理解，node、value、pointer、previousNode、nextNode这些个概念都还挺直观的，但是后半段需要稍微多咀嚼几遍才能绕明白，总之就是不够白话，甚至有点枯燥。不过，既然这是一个主张在轻松愉悦氛围下学习的文科生专栏，当然还是说人话比较有意思。要让我说，就直接拿火车来举例好了

（提示：以下内容可能有点中二，看不看随你，不想看的话从目录直接跳去看代码就行。）

基本结构

双链表这种数据结构呢，就像火车车厢一样，一节连着一节，每一节都有它的前一节（previous）和后一节（next）（注意这绝对不是废话，如果你仔细想想的话）。

假设我们现在正乘坐着一列刚从列车工厂（双链表构造类 DoublyLinkedList Class）下线，名为“双链表号”由5节车厢组成的列车组（双链表实例对象 new DoublyLikedList() ），前往目的地为数据结构与算法的极乐净土。我们分别用A-B-C-D-E（value）来表示每一节车厢（node），比如其中B车厢的前一节（previous）是A车厢，后一节（next）是C车厢。但是这些都不是重难点，因为双链表只是“看上去像”一列火车而已，它和普通的火车有一个本质的区别，这一点比前面这些概念都重要！

讲个恐怖故事，你以为这列看上去风平浪静的“双链表号”列车组的车头（head）是A，车尾（tail）是E对吗？这么理解似乎也没什么问题，因为双链表的head属性的确是A，tail属性也的确是E，但问题就出在头（head）并不是真正意义上的“头”，尾（tail）也并不是真正意义上的“尾”。这列特殊的列车组“真正的车头”（我也不知道专业术语叫啥，就用start来表示吧）根本就不是A，“真正的车尾”（用end来表示）也根本就不是E。为什么呢？因为，它是一列——无头无尾的幽灵列车！（start和end都为null）。我们肉眼能看到的，以为是车头的A车厢前面（previous）其实还挂了一节真正的车头——幽灵车厢null，只是出于某种原因，我们普通人根本就感知不到它的存在。同样，你以为是车尾的E车厢后面（next），其实也还挂了另一节真正的车尾——幽灵车厢null（null--A--B--C--D--E--null）。哪怕受到某种超自然力量的作用，整个列车组被吞噬到只剩下唯一一节车厢C，那么C车厢也是夹在两个幽灵车厢null中间的（此时C既是head又是tail，在结构上长这个样子：null--C--null），除非它也被毁灭了

OK，咱接着往下捋：

两个节点链接允许在任一方向上遍历列表。

在双向链表中进行添加或者删除节点时,需做的链接更改要比单向链表复杂得多。这种操作在单向链表中更简单高效,因为不需要关注一个节点（除第一个和最后一个节点以外的节点）的两个链接,而只需要关注一个链接即可。

至于单链表咱回头再说，总之双链表需要比单链表多维护一个previous，与之相对应的增加（insertion）和删除（deletion）操作显然就会更复杂一些。

基本操作方法

增

比如出于某种原因，哪一天这个“双链表号”列车组需要增加一节车厢F，也就是往E的后面（next），幽灵车尾null的前面（previous）连一节新车厢的话，就需要完成这样一系列的操作：请来个能看到幽灵车尾null的超能力者，把链接着E和null的那个“隐形铰链”拆了跟null一起先揣兜里，换个麻瓜也能看到的那种实体铰链，用这个新的铰链往E的后面（next）挂上新车厢F（傻子都知道，F前面（previous）的那一节肯定是E）。然后，从兜里掏出刚才拆下来的隐形铰链和null，在F的后面（next）隐形铰链挂上null。

当然，也可以在中间任意位置插入新的node，比如新增一个value为D2的车厢，也就是往D的后面（next）E的前面（previous）插入，这时候的操作方法本质上跟刚才那种差不多，只不过没有隐形铰链和幽灵车厢（null）了，只需要把D跟E先解除链接，加个新的铰链然后给这俩中间挂上D2就行。这一顿操作下来，差不多就相当于双链表的插入（ append(value) ）操作的实现过程。

除了append(value)这种往任意指定位置插入的操作，双链表还有一种类似于新加个“车头”（一般人能看见的那个）的那种头部插入（ prepend(value) ）操作。整个操作过程就不多废话了，类比一下上面那段内容，懂的都懂。

删

接下来说说删除（deletion）操作，这个就厉害了。双链表共有三种删除操作方法，分别是掐头（ deleteHead() ）、去尾（ deleteTail() ）、指哪儿删哪儿（ delete(value) ）。从参数也能看出个名堂来，前两种没参数的方法就是最简单的掐头去尾操作，也没必要举例子了。重点是最后一种delete(value)，跟刚才的append一样，同样需要我们传入一个参数value比如C，把C这节车厢给揪出来，拆掉它前（previous）后（next）的铰链，把他前面的（previousNode）和后面的（nextNode）车厢重新链接起来。至于这个被开除车籍的倒霉蛋C嘛（C语言：勿cue…），就让它自生自灭去吧，不管是被外星人带走还是被炸毁到灰都不剩的那种。

查

双链表除了刚才提到的增、删操作之外，当然还有最基本的查（find）操作，不过因为比较简单就先不举例了，一会儿直接看代码分析就行。

改（没这种操作️）

没错，双链表的确没有一个直接类似于Map的set方法或者对象的setter那种改操作，原因也很好理解，就像是你没法把C车厢直接原地变成一个新的V车厢一样。想实现类似改功能的话，也只能通过删和增配合着来了，需要从头（head）或者尾（tail），多做几轮删+增的交叉操作，最终达到同样的效果，比起HashMap什么的，这种操作的复杂度自然会高一些，不过毕竟这个数据结构本身被设计出来也不是专门拿来干这事儿的。

逆向

虽然双链表的结构决定了它没法实现原地替换，但它可以轻松实现原地逆向（reverse），就像小学语文里我们伟大的中国铁路之父詹天佑发明的双头列车一样，直接把车尾当车头（head），车头当车尾（tail），所有的前（previous）后（next）关系都反转一下就行。

其他方法 

最后，除了增删查这些基本方法，双链表还可以有包括但不限于toArray、fromArray、toString这种输出类的“附赠品”方法，当然你也可以根据个人喜好自行扩充别的啥方法。

复杂度

最后来看一下双链表的复杂度：

时间复杂度

Access	Search	Insertion	Deletion
O(n)	O(n)	O(1)	O(1)

空间复杂度

O(n)

双链表的空间复杂度为O(n)，而从时间复杂度上来看，双链表的增（insertion）、删（deletion）操作都具备最低的常数级复杂度，所以它也就挺适合被拿来做LRU缓存算法的。

双链表的概念、基本构成、基本实现和相关操作方法实现差不多就是这些了，下面进入激动人心的coding环节，如果你不看前面那些，直接跳过来看也完全OK。

---

代码篇

双向链表节点构造类DoublyLinkedListNode

实现方式

要完整实现一个双链表构造类，需要先实现一个双链表节点（doubly linked list node）的构造类DoublyLinkedListNode，下面是用ECMAScript 6的class来实现这个DoublyLinkedListNode构造类的方法。

export default class DoublyLinkedListNode {
  constructor(value, next = null, previous = null) {
    this.value = value;
    this.next = next;
    this.previous = previous;
  }

  toString(callback) {
    return callback ? callback(this.value) : `${this.value}`;
  }
}

因为它只是一个最简单的node模型，所以代码也就这么几行。首先，DoublyLinkedListNode的构造方法中包含value、next、previous三个基本属性，每个属性分别是用来干嘛的大家肯定也都懂。除此之外还有一个用来把value属性转为字符串输出的toString方法，这个方法有一个可选参数callback，用来实现自定义格式化的value字符串输出。

双向链表构造类DoublyLinkedList

构造方法

接下来进入正式环节，来看看双链表的构造类DoublyLinkedList的实现方式：

import DoublyLinkedListNode from './DoublyLinkedListNode';
import Comparator from '../../utils/comparator/Comparator';

export default class DoublyLinkedList {
  /**
   * @param {Function} [comparatorFunction]
   */
  constructor(comparatorFunction) {
    /** @var DoublyLinkedListNode */
    this.head = null;

    /** @var DoublyLinkedListNode */
    this.tail = null;

    this.compare = new Comparator(comparatorFunction);
  }
  ...
}

首先来看看构造方法，一个双链表的构造方法中包含两个分别代表头节点和尾节点的属性head和tail，还有一个通过我们引入的Comparator类实例化出来的方法compare，方便用来做后续操作中的比较运算。

那就顺便让我们看看这个Comparator类里面都有哪些好康的。

export default class Comparator {
  /**
   * Constructor.
   * @param {function(a: *, b: *)} [compareFunction] - It may be custom compare function that, let's
   * say may compare custom objects together.
   */
  constructor(compareFunction) {
    this.compare = compareFunction || Comparator.defaultCompareFunction;
  }

  /**
   * Default comparison function. It just assumes that "a" and "b" are strings or numbers.
   * @param {(string|number)} a
   * @param {(string|number)} b
   * @returns {number}
   */
  static defaultCompareFunction(a, b) {
    if (a === b) {
      return 0;
    }

    return a < b ? -1 : 1;
  }

  /**
   * Checks if two variables are equal.
   * @param {*} a
   * @param {*} b
   * @return {boolean}
   */
  equal(a, b) {
    return this.compare(a, b) === 0;
  }

  /**
   * Checks if variable "a" is less than "b".
   * @param {*} a
   * @param {*} b
   * @return {boolean}
   */
  lessThan(a, b) {
    return this.compare(a, b) < 0;
  }

  /**
   * Checks if variable "a" is greater than "b".
   * @param {*} a
   * @param {*} b
   * @return {boolean}
   */
  greaterThan(a, b) {
    return this.compare(a, b) > 0;
  }

  /**
   * Checks if variable "a" is less than or equal to "b".
   * @param {*} a
   * @param {*} b
   * @return {boolean}
   */
  lessThanOrEqual(a, b) {
    return this.lessThan(a, b) || this.equal(a, b);
  }

  /**
   * Checks if variable "a" is greater than or equal to "b".
   * @param {*} a
   * @param {*} b
   * @return {boolean}
   */
  greaterThanOrEqual(a, b) {
    return this.greaterThan(a, b) || this.equal(a, b);
  }

  /**
   * Reverses the comparison order.
   */
  reverse() {
    const compareOriginal = this.compare;
    this.compare = (a, b) => compareOriginal(b, a);
  }
}

Comparator类其实就是一个封装了一系列比较算法的工具类，它有一个构造方法compare，可以通过传入的​​​​​​​compareFunction参数来自定义比较算法函数，如果不传这个参数则使用Comparator类上的静态方法defaultCompareFunction（比较两个值，如果相等就返回0，前面的小于后面的就返回-1，反之则返回1）作为默认的比较算法。Comparator类所封装的几个普通方法包括相等（equal）、小于（lessThan）、大于（greaterThan）、小于等于（lessThanOrEqual）、大于等于（greaterThanOrEqual），此外还有一个用于交换俩参数反转比较顺序的方法reverse。

回到刚才的DoublyLinkedList类，接着看它最重要的几个增删查方法各自的具体实现。

增方法 prepend(value)

​​​​​​​首先来看看头部插入操作的方法prepend(value)：

  /**
   * @param {*} value
   * @return {DoublyLinkedList}
   */
  prepend(value) {
    // Make new node to be a head.
    const newNode = new DoublyLinkedListNode(value, this.head);

    // If there is head, then it won't be head anymore.
    // Therefore, make its previous reference to be new node (new head).
    // Then mark the new node as head.
    if (this.head) {
      this.head.previous = newNode;
    }
    this.head = newNode;

    // If there is no tail yet let's make new node a tail.
    if (!this.tail) {
      this.tail = newNode;
    }

    return this;
  }

prepend方法接收一个任意类型的参数value，返回执行完头部插入操作后的双链表实例对象自身，方便后续操作的链式调用。

增操作的第一步自然是先创建实例，也就是使用我们刚才引入的双链表节点构造类DoublyLinkedListNode，创建一个node实例对象newNode。该实例对象的value和head属性分别为prepend方法参数传入的value，以及这个链表构造方法内的头属性head。

接下来需要有一个条件判断。如果我们的双链表没有头（自然也就没有尾）也就是空链表的话，那就给它增加个头（也是尾），把head属性设为这个新创建的node实例对象newNode，相反如果它有头，那就把原来的头节点的上一个节点（head.previous）指向新增加的这个节点，也就是将head的previous属性设为newNode。另外，如果这个双链表没尾（tail），那就把新增加的这个节点同样作为尾，也就是将tail属性也设为newNode，就是之前例子中提到的那个只剩下一节车厢的情况。

增方法 append(value)

双链表的另一个增方法，append(value)：

 /**
   * @param {*} value
   * @return {DoublyLinkedList}
   */
  append(value) {
    const newNode = new DoublyLinkedListNode(value);

    // If there is no head yet let's make new node a head.
    if (!this.head) {
      this.head = newNode;
      this.tail = newNode;

      return this;
    }

    // Attach new node to the end of linked list.
    this.tail.next = newNode;

    // Attach current tail to the new node's previous reference.
    newNode.previous = this.tail;

    // Set new node to be the tail of linked list.
    this.tail = newNode;

    return this;
  }

可以看到，append和prepend这俩方法其实都差不多，无非就是多了个往中间某个位置插入的情况，需要修改前序和后续两个相邻节点分别的next和previous指向。当然，使用append也能做往头部插的操作。

删方法 delete(value)

双链表最厉害的删方法delete(value)，这块重点看下：

  /**
   * @param {*} value
   * @return {DoublyLinkedListNode}
   */
  delete(value) {
    if (!this.head) {
      return null;
    }

    let deletedNode = null;
    let currentNode = this.head;

    while (currentNode) {
      if (this.compare.equal(currentNode.value, value)) {
        deletedNode = currentNode;

        if (deletedNode === this.head) {
          // If HEAD is going to be deleted...

          // Set head to second node, which will become new head.
          this.head = deletedNode.next;

          // Set new head's previous to null.
          if (this.head) {
            this.head.previous = null;
          }

          // If all the nodes in list has same value that is passed as argument
          // then all nodes will get deleted, therefore tail needs to be updated.
          if (deletedNode === this.tail) {
            this.tail = null;
          }
        } else if (deletedNode === this.tail) {
          // If TAIL is going to be deleted...

          // Set tail to second last node, which will become new tail.
          this.tail = deletedNode.previous;
          this.tail.next = null;
        } else {
          // If MIDDLE node is going to be deleted...
          const previousNode = deletedNode.previous;
          const nextNode = deletedNode.next;

          previousNode.next = nextNode;
          nextNode.previous = previousNode;
        }
      }

      currentNode = currentNode.next;
    }

    return deletedNode;
  }

delete方法接收一个任意类型的参数value，返回的不是一双链表实例对象本身，而是被删的那个node对象，返回值形式类似于Array的pop和shfit操作。

首先判断一下双链表有没有头，没的话直接返回一个null，表示啥都没删到。接下来先分别声明两个临时变量：

deleteNode —— 初始值为null，用来指向将被删除的node对象。

currentNode —— 初始值为head，用来标记从头遍历整个链表的当前进度。

接下来就是删方法delete的核心实现。我们从头（head）开始遍历整个链表，通过比较当前currentNode的value属性与传参进来的value是否相等，来匹配整个链表中需要被删除的node元素。如果找到了目标node，就把deleteNode从指向null改为指向currentNode。找到了要删除的node元素只是一个开始，接下来在不同情况下的后续操作才是我们最应该关注的。

找到目标node之后，有三种不同的情况等着我们去处理。

CASE 1⃣️ 要删的是头

如果要删的目标节点是头节点（head），就把双链表的head重新指向deleteNode的next属性所表示的节点，也就是原来的头节点（head）后面的那个节点（deleteNode.next or head.next ）成为了新的头节点（head）。如果删完之后链表中还有头节点（head），也就是删除之前链表至少有两个节点，就把头节点的上一个​​​​​​​（head.previous）指向null。接下来，这里还有一种特殊情况之前没有提到，因为无论参数value还是各节点的value属性都没有唯一性限制，那么肯定也存在这样一种情况——整个链表上有所有节点的value属性跟要删除的目标节点的value值一样，这种情况的判断条件等价于deleteNode === this.head && deleteNode === this.tail。如果碰到这种情况，我们就得把所有一样的node都给它一口气删光，这里就可以非常果断地直接执行this.tail = null，这也能说明为啥双链表删操作的时间复杂度可以做到这么低。

CASE 2⃣️ 要删的是尾

如果要删的目标节点是尾节点（tail），那好说，直接把尾节点改为要删的目标节点的前序节点（deleteNode.previous），再把尾节点的后续指向null就行了。

CASE 3⃣️ 要删的在头和尾之间

如果要删的目标节点在头和尾之间，这种情况涉及的操作前面的例子里也有说到过，也比较好实现，只需分别修改要删的目标节点的前序节点（deleteNode.previous）的next指向，以及后续节点的previous指向即可。

删方法 deleteHead()

双链表掐头去尾操作之掐头，实现如下：

  /**
   * @return {DoublyLinkedListNode}
   */
  deleteHead() {
    if (!this.head) {
      return null;
    }

    const deletedHead = this.head;

    if (this.head.next) {
      this.head = this.head.next;
      this.head.previous = null;
    } else {
      this.head = null;
      this.tail = null;
    }

    return deletedHead;
  }

掐头去尾操作方法都不需要参数，具体的删方法实现也没啥可说的。没头就return null，只有一个节点就把头尾都指向null形成一个空链表，有两个以上节点的话就把链表的第二个节点变成头，最后返回被删的头节点。

删方法 deleteTail()

双链表掐头去尾操作之去尾，实现如下：

  /**
   * @return {DoublyLinkedListNode}
   */
  deleteTail() {
    if (!this.tail) {
      // No tail to delete.
      return null;
    }

    if (this.head === this.tail) {
      // There is only one node in linked list.
      const deletedTail = this.tail;
      this.head = null;
      this.tail = null;

      return deletedTail;
    }

    // If there are many nodes in linked list...
    const deletedTail = this.tail;

    this.tail = this.tail.previous;
    this.tail.next = null;

    return deletedTail;
  }

去尾操作deleteTail和掐头操作大差不差。没头就return null，只有一个节点就把头尾都指向null，有两个以上节点就把倒数第二个节点变成尾节点，最后返回被删的尾节点。

查方法 find(value)

双链表唯一的查方法find之前没举例，直接看实现吧：

  /**
   * @param {Object} findParams
   * @param {*} findParams.value
   * @param {function} [findParams.callback]
   * @return {DoublyLinkedListNode}
   */
  find({ value = undefined, callback = undefined }) {
    if (!this.head) {
      return null;
    }

    let currentNode = this.head;

    while (currentNode) {
      // If callback is specified then try to find node by callback.
      if (callback && callback(currentNode.value)) {
        return currentNode;
      }

      // If value is specified then try to compare by value..
      if (value !== undefined && this.compare.equal(currentNode.value, value)) {
        return currentNode;
      }

      currentNode = currentNode.next;
    }

    return null;
  }

find方法接收一个对象类型的可选参数findParams，该对象有两个属性——表示要查的value值的value（任意类型，默认值undefined），以及自定义遍历方法callback（function类型，默认值undefined）。find方法的返回值为从链表中查到的那个节点对象。如果没有头就不查了，直接返回null。接下来声明一个临时变量currentNode作为从头（head）到尾遍历整个链表的进度标记。

如果findParams的value属性有设置，就比较当前currentNode的value属性与findParams的value属性是否相等，是的话直接返回currentNode。

如果findParams还设置了一个合法的callback属性，就使用这个callback方法处理当前currentNode节点的value属性，最终返回currentNode。

如果找不到需要匹配的节点就返回null。

逆向方法reverse()

之前也有看到过，The two node links allow traversal of the list in either direction. 逆向也是双向链表的一个特色功能，实现如下：

  /**
   * Reverse a linked list.
   * @returns {DoublyLinkedList}
   */
  reverse() {
    let currNode = this.head;
    let prevNode = null;
    let nextNode = null;

    while (currNode) {
      // Store next node.
      nextNode = currNode.next;
      prevNode = currNode.previous;

      // Change next node of the current node so it would link to previous node.
      currNode.next = prevNode;
      currNode.previous = nextNode;

      // Move prevNode and currNode nodes one step forward.
      prevNode = currNode;
      currNode = nextNode;
    }

    // Reset head and tail.
    this.tail = this.head;
    this.head = prevNode;

    return this;
  }

从头到尾线性遍历整个链表，把每个节点上的next和previous指向互换一下，头和尾互换一下，就是逆向操作的实现方式。

其他方法

双链表还有几个其他的补充方法，实现如下：

  /**
   * @return {DoublyLinkedListNode[]}
   */
  toArray() {
    const nodes = [];

    let currentNode = this.head;
    while (currentNode) {
      nodes.push(currentNode);
      currentNode = currentNode.next;
    }

    return nodes;
  }

  /**
   * @param {*[]} values - Array of values that need to be converted to linked list.
   * @return {DoublyLinkedList}
   */
  fromArray(values) {
    values.forEach((value) => this.append(value));

    return this;
  }

  /**
   * @param {function} [callback]
   * @return {string}
   */
  toString(callback) {
    return this.toArray().map((node) => node.toString(callback)).toString();
  }

这些就不说了，很简单的几个遍历操作，当然也可以再自行扩充一些新的实用方法。

关于JavaScript中双向链表（doubly linked list）的所有内容就先写到这儿吧，字数也有点多了，能耐心看到这儿的肯定都是真爱了。那LRU缓存算法的内容就放到下篇去展开吧，先列个基本大纲——下篇将继续使用通俗易懂的文字来讲述LRU缓存算法的概念、核心价值观、基本原理和前后端应用场景，以及通过两种方式实现一个能满足基本使用的LRU缓存算法，其中一种就会用到本篇中的双向链表来实现。如果你着急着想了解LRU缓存算法，就用我开篇提到的那个开源项目去学习吧，可以多跑几遍jest测试案例强化理解。（本篇完）