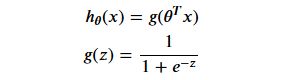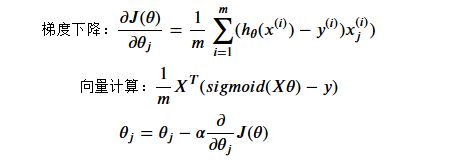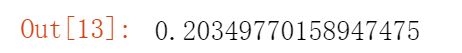逻辑回归【保姆级注释Python实现】

1. 引入头文件

import pandas as pd
import numpy as np
import matplotlib.pylab as plt
import scipy.optimize as opt

2. 读取数据

百度网盘地址如下：

链接：https://pan.baidu.com/s/12iVi93AQStYRmgUhhYR0Zg 提取码：9kgk

# 根据自己存放的路径进行修改
path='ML-homework-main\ex2-logistic regression\ex2data1.txt'
data=pd.read_csv(path,header=None,names=['Exam1','Exam2','Admitted']
# 查看效果图【这种查看方式只能再jupyter中使用】
data.head()

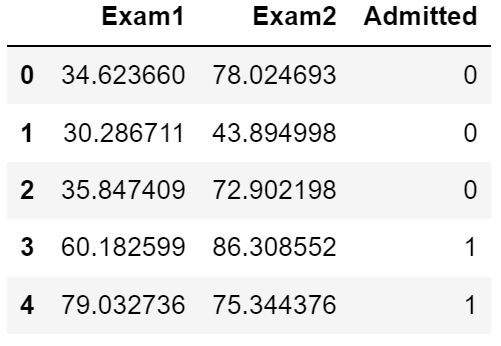
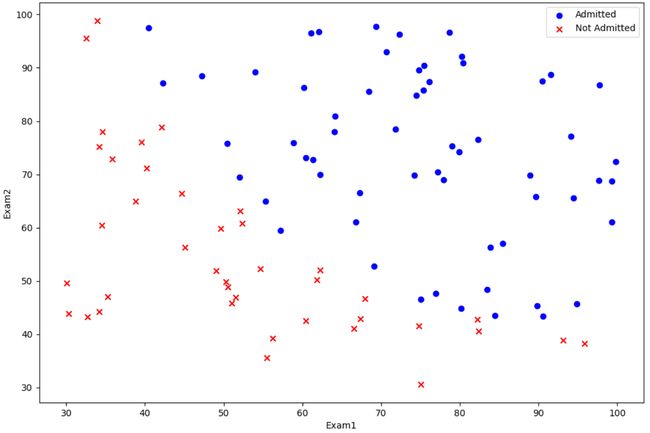
3. 绘制样本

# 将Admitted为1的部分提出来，组成positive
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]

plt.figure(figsize=(12, 8))
# 头两个参数是X轴与Y轴数据，c是颜色，marker是散点图形状
plt.scatter(positive['Exam1'], positive['Exam2'],c='b',marker='o',label='Admitted')
plt.scatter(negative['Exam1'], negative['Exam2'],c='r',marker='x',label='Not Admitted')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.legend(loc=True)
plt.show()

4. sigmoid函数

在二分类问题中，Y取值只可能是0或1，激活函数很好满足了这个特点，当X越大，Y越接近1，换一种说法即X越大越可能取1，因此我们选其作为分类问题中的拟合函数

其中sigmoid的参数仍然采用线性表达的形式

# g(z)，z越大越靠近1，z越小越靠近0
def sigmoid(z):
    return 1/(1+np.exp(-z))

4.1 绘制sigmoid图形

# 取[-10,10]之间的数作为x轴，步距为0.5
num=np.arange(-10,10,step=0.5)
plt.plot(num,sigmoid(num),'r')
plt.show()

5. 代价函数

代价函数的作用是使预测结果出错时给予惩罚，正确时给予奖励

如Y现实中应该为1，但是预测结果却为0，此时代价函数值应该很大，起惩罚作用，让操作者知道预测出现问题；反之，若预测正确，代价函数值应该很小，起奖励作用，让操作者知道预测问题不大
总之代价函数值反映了预测结果的准确程度，我们希望它越小越好

为何此处代价函数不选用常见的平方损失函数，而要选这么复杂的形式？

1. 代价函数的选择与拟合函数有关，此处拟合函数为激活函数，代入平方损失函数中得到的代价函数无法确定是否为凸函数，因此不一定能找到最优解，同时由于激活函数中有指数项，若后期需要对代价函数进行求导等操作时不好处理

2. 根据我们的计算习惯，通常有指数项的都需要用一个对数对其进行处理，方便操作。同时我们也可以发现，上述代价函数在Y取0或1时是截然不同的结果，实则是将两段函数整合为一个函数。

3. 由于激活函数取值h必定处于(0,1)，因此对于-ln(h)以及-(ln(1-h))也仅仅关注其(0,1)范围上的取值情况，为了便于观察函数取值情况，先暂时忽略与取值情况无关的累加符以及i上标

4. 当预测值Y==1时，J(θ)=-ln(h)，此时h越靠近1，J(θ)越靠近0，即预测正确时，代价很小

   反之，当h越靠近0，J(θ)越靠近+∞，即预测错误时，代价很大

5. 当预测值Y==0时，J(θ)=-ln(1-h)，此时h越靠近1，J(θ)越靠近+∞，即预测错误时，代价很大

   反之，当h越靠近0，J(θ)越靠近0，即预测正确时，代价很小

由此可以得出结论，此代价函数是一个凸函数【即可用梯度下降法迭代θ】，表达式方便求导等运算，也保证了在预测正确时给予奖励，预测错误时给予惩罚，由此我们选择其作为代价函数。

# 代价函数
def cost(theta, X, Y):
    # [email protected]即当前的预测值|
    first = Y*np.log(sigmoid(X@theta.T))
    second = (1-Y)*np.log(1-sigmoid(X@theta.T))
    return -1*np.mean(first+second)

6. 梯度下降

J(θ)对θj求偏导的推导过程

其中向量计算是梯度下降的矩阵表示，1/m二者相同不多做解释，主要解释后面部分为何一致，解释如下【最好辅助画图理解】：

1. 首先把目光移到向量计算中括号内的元素：

• $X$矩阵行向量代表样本，列向量代表特征，一行一样本，一列一特征
• $X\theta$即每一个样本值与参数向量$\theta$进行线性组合，得到的是每一个样本值在当前参数$\theta$下的预测值，其最终结果是向量，规模与结果$Y$一致，因此减去$Y$后仍然是$m$维列向量，记作$\beta$
• $X^T$则与$X$正好相反，一行一特征【每行的值分别为$x_j^i,x_j^{i+1}...$】，一列一样本
• 所以整体相乘的结果为一个列向量$\alpha$，规模与$\theta$一致，每一维代表一个$J(\theta )$对${\theta }_j$求导的取值

2. 再将目光转回梯度下降公式：

• 每进行一次$h-y$计算对应$\beta$【$\beta$上边有提及其形状】的一维元素，再乘上$x_j^i$实则等同于乘上$X^T$一行的一个元素【按顺序进行计算】。
• 按如上规则进行累加，即对应$\alpha$的第一维的值，其为$J(\theta )$对${\theta }_0$求导的结果，以此类推，对不同的${\theta }_j$求导值分别存储在$\alpha$的不同维度中
• 由此证明，向量计算的公式与梯度下降的公式完全一致

注意⚠！！！这仅仅是求导的处理，并没有真正实现梯度下降，若要实现真正梯度下降还需要确定迭代次数、学习率等

# 梯度下降的向量计算表示
def gradient(theta, X, Y):
    # 结果返回J(θ)对不同θj的的求导结果
    return 1/len(X)*X.T@(sigmoid(X@theta.T)-Y)

7. 数据预处理

# 由于激活函数参数仍然采用线性表示，因此需要填充一列1，使线性表达式能用矩阵向量表示
data.insert(0,'Ones',1)
# 行全取，列只有最后一列不取
X=data.iloc[:,0:-1].values
# 行全取，列只取最后一列，保证Y是一维的，否则cost函数会出错
Y = data.iloc[:, -1].values
# 在当前数据下只需要3个θ，theta初始值全0，是行向量
theta=np.zeros(3)

8. 检查已写好的函数是否能正常运行

# 观察初始θ值对应的预测函数
# 发现代价函数为0.69，说明准确率还不赖！【瞎猫碰上死耗子】
cost(theta,X,Y)

# J(θ)对不同θ进行求导后的取值
gradient(theta,X,Y)

9. 拟合参数【得到拟合后的$\theta$】

此处实现梯度下降我们使用scipy.optimize包中内置方法进行实现，不再像刚学梯度下降时手动编写函数进行迭代，若有需求可看此文章

机器学习之梯度下降

# func是要最小化的函数【代价函数】
# x0是最小化函数的自变量【θ值】
# fprime是最小化的方法【梯度下降】
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, Y))
# 看看result是啥，发现result[0]是你和后的θ
result

# 此时result[0]中存放的就是根据目前算法得出的θ最优解
# 更新θ值
theta=result[0]
# 看看当前cost值，发现代价值相对于前面的0.68更小了，说明预测准确率进一步上升
cost(result[0],X,Y)

10. 预测分析

此时我们已经得到了$\theta$值，只需要带回h函数即可得到预测情况

根据$\theta$进行预测：$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}X}}$

$h_{\theta }\ge 0.5$, 预测$y=1$

$h_{\theta }<0.5$, 预测$y=0$

# 预测函数
def predict(theta, X):
    # 得到m个预测值
    probability = sigmoid(X @ theta.T)
    # 如果预测值大于等于0.5，则预测为1；反之预测为0
    return [1 if x >= 0.5 else 0 for x in probability]

# predictions存放当前X对应的预测值
predictions = predict(np.matrix(theta), X)
# ^是异或符号，二者同说明预测成功，此时为异或值0，在correct中标记为1
# zip函数起打包作用，即同时从predictions，Y中取对应元素a,b
correct = [1 if a^b == 0 else 0 for (a,b) in zip(predictions, Y)]
# 预测正确的长度除总长度即预测准确率
accuracy = (sum(correct) / len(correct))
print(f'accuracy = {accuracy*100}%')

11. 决策边界

我们知道，在激活函数$h(x)$中，如果$x>0$，则$y$被预测为$1$，反之预测为$0$，因此$x=0$就是一个分界线

而在我们的模型中，激活函数的参数是由${\theta }^{T}X$来表示的，因此如果我们令${\theta }^{T}X=0$并画出这条直线，则会在散点图中呈现出分界线的效果，分界效果的好坏与预测准确率相关

${\theta }^{T}X=0$

${\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2=0$

$x_2=-(\frac{{\theta }_0}{{\theta }_2}{x}_0+\frac{{\theta }_1}{{\theta }_2}{x}_1)$

其中$x_0$是我们为了便于矩阵计算所加上去的，其值恒为$1$

$\because$我们画图以$x_2$为纵坐标，$x_1$为横坐标

$\therefore x2$对应我们认知中的$y$轴，$x_1$对应我们认知中的$x$轴

# 结果为三个θ都除θ2再乘-1，结果由列表保存
coef=-(theta/theta[2])
# x取值为[30,100]，步幅为0.5
x=np.arange(30,100,0.5)
# θ0对应参数为x0，而x0恒为1；θ1对应参数为x1
y=coef[0]+coef[1]*x

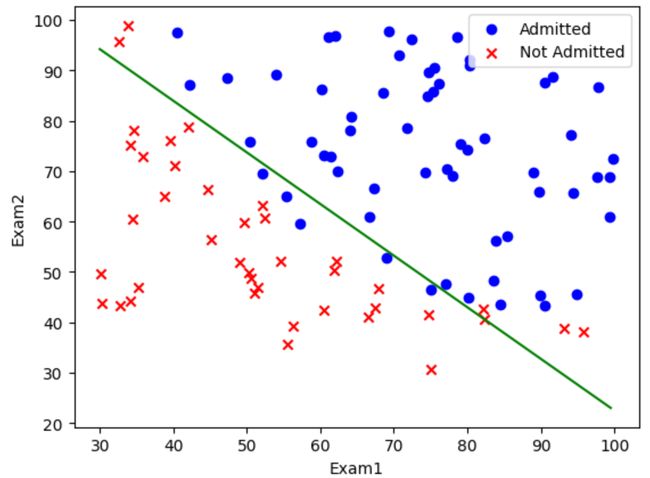
12. 绘制决策边界

终于来到最后一步了！！！

# 头两个参数是X轴与Y轴数据，c是颜色，marker是散点图形状
plt.scatter(positive['Exam1'], positive['Exam2'],c='b',marker='o',label='Admitted')
plt.scatter(negative['Exam1'], negative['Exam2'],c='r',marker='x',label='Not Admitted')
# 传入x与y数据绘制折线图
plt.plot(x,y,c='g')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.legend(loc=True)
plt.show()

13. 写在最后

本文代码主体来自于这位大佬的笔记吴恩达机器学习笔记，在此基础上加上了自己对于一些代码的注释从而更加方便理解，本人是新手入门，有错误在所难免，望各位不吝赐教。若本文对于你理解逻辑回归有些许帮助，也不妨给个赞鼓励一下，你们的支持是我创作最大的动力！