数据结构-----Trie树

Trie树

Trie树，又称字典树，前缀树，单词查找树。是字符串算法中一个比较基础的结构。在字符串查找方面有着线性时间的查找速度，是因为查找时间与Trie中的数据总量无关，只与待查找的字符串的长度有关。

字典树可以应用在多数字符串查找问题上，
比如说，给定一个非常大的文本，文本中每一行是一个单词，然后查询文本中是否包含某个单词，或者询问某个单词出现的次数。
再比如Trie + KMP算法就构成了AC自动机，可以实现多模式匹配问题。
当然首先，需要学会如何构建一棵Trie树。

Trie树的思想是利用词的公共前缀进行存储，这也正是树结构天生自带的优势，两个词具有公共前缀就意味着具有相同的父节点，而公共前缀就是从根节点到父节点这条路径所表示的内容。
Trie树的构建有array和linked-list两种，本文只介绍利用数组构建的方法。

Trie树节点

要构建一棵Trie树，首先应该解决的问题是，如何定义树节点。
假设Trie树只存储英文单词，只由26个小写英文字母组成，那么从一个节点出发，就有26种可能，也就是每个节点都有26个孩子节点（如果某个节点表示的是字符a，那么紧接着它的字符可能是a,b,c,d,e,…,z中的任何一个，因为英文单词有很多种）。

注：但是因为开辟的大小是事先规定好的，所以能够存储的范围非常有限。如果想要存储中文字符，可以使用《双数组Trie数》。

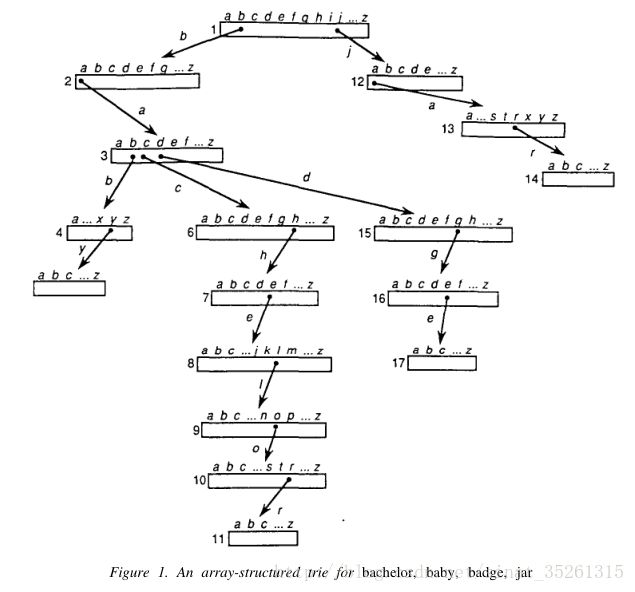
如图，每个节点表示一个英文字母，同时每个节点又有26个孩子节点，这些孩子节点分别表示从a到z的英文字母。这样，当从根节点沿着一条路径走下来后，将所有经过的节点表示的字母连接起来，就是一个完整的英文单词。

另外需要注意的是，构造Trie树时是每次插入一个完整的单词，所以只有当沿着某条路径走到特定节点后，连接起来的单词才是完整的单词，所以在每个节点中需要有一个bool型变量记录从根节点到当前结点这条路径表示的单词是否存在。

这样就可以为每一个树节点都开辟一个数组来存储孩子节点指针，像这样：

const size_t LETTER_SIZE = 26;

class TrieNode
{
public:
    TrieNode(const char& pAlpha = '\0'):
        m_pAlpha(pAlpha),
        m_pExist(false),
        m_pString("")
    {
        m_pNext = new TrieNode*[LETTER_SIZE];
        for(size_t i = 0; i < LETTER_SIZE; ++i)
            m_pNext[i] = NULL;
    }
    char m_pAlpha;
    bool m_pExist;  //记录从根节点到当前结点所构成的字符串是词典中的单词
    string m_pString;   //记录从根节点到当前结点所构成的字符串(单词），只有当m_pExist为true时该变量才有实际意义
    TrieNode **m_pNext;  //存储孩子节点指针的数组
}

在实际应用中，还可以根据需要为TrieNode增加多个成员变量，比如说

size_t m_pNextSize; //记录next数组中有多少个非空指针，即有多少个孩子不是NULL
size_t m_pCount; //在统计某个单词出现次数时使用

定义中将m_pNext数组中的每一元素都设置成NULL，表示这个节点没有孩子节点，也就是没有其它英文字母在它的后面。而且为了简便，可以认为表示a到z的孩子节点在next数组中是按顺序存储的，这样因为小写字母a到z的ASCII码是从97开始的，所以在m_pNext数组内想要确定哪个单词存在，就可以直接判断m_pNext[pAlpha - 97]是否是NULL即可。pAlpha可以是从a到z的任意字符。
像这样：

//想要判断pNode节点后面是否还有表示字符b的节点
if(pNode->m_pNext['b' - 97] != NULL)
    return true;
else
    return false;

注：对于上面的第二张图，根节点的左孩子节点表示字符a，它的26个孩子节点中只有表示字符b,d,f的节点存在。所以很显然利用数组表示的Trie会存在大量的空间浪费。
另外可能也注意到了Trie树的根节点root，它不表示任何字符，只用来分出不同的字符。

对于Trie树，构建操作主要就是将词典中的单词拆成一个个字符，每个字符申请一个节点，后一个字符作为前一个字符的孩子。当申请完一个单词的所有节点后，需要把最后一个节点的m_pExist设置成true，表示从根到目前节点所表示的字符串在词典中存在。

插入函数

在Trie树的类中，使用insert()函数实现上述对每个单词处理然后添加的操作

class Trie
{
public:
    Trie();
    ~Trie();

    void insert(const string& pKey); 
    bool exist(const string& pKey);
private:
    TrieNode *m_pRoot;
}

插入函数的思路如下：
1.先判断是否已经申请了前缀部分的节点，因为具有公共前缀的单词只有一份前缀。例如上面的”abc”，”ada”和”af”，三者具有相同的前缀’a’，所以在添加”abc”后添加”ada”时，就不需要再为第一个字符’a’申请节点了，直接移动到字符’a’，为表示字符’a’的节点申请表示字符’d’的孩子。”af”也是如此。
2.不断遍历，如果存在当前要申请的节点，则不用再次申请内存，直接移动到那个位置。
3.为最后一个节点的exist变量赋值为true。

代码实现如下：

void Trie::insert(const string& pKey)
{
    TrieNode* pNode = m_pRoot; //从根节点开始寻找是否已经申请了某些节点
    for(size_t i = 0; i < pKey.length(); ++i)
    {
        char pAlpha = pKey.at(i);
        //如果当前结点没有表示pAlpha的孩子节点时，申请节点
        if(pNode->m_pNext[pAlpha - 97] == NULL)
        {
            TrieNode *ppNode = new TrieNode(pAlpha);
            pNode->m_pNext[pAlpha - 97] = ppNode;
        }
        //移动到表示pAlpha的节点，继续申请
        pNode = pNode->m_pNext[pAlpha - 97];
    }

    //将最后一个节点的m_pExist变量设置为true，表示单词存在
    pNode->m_pExist = true;
    pNode->m_pString = pKey;
}

判断某个字符串是否出现在词典中

insert函数是用于构造Trie树，而exist函数则是为了解决给定文本文件，每行为一个单词，然后给定一个单词问是否在其中出现的问题。首先需要将文本文件读入，将每一行的单词使用insert函数插入到Trie树中，然后进行查询。因为使用的是数组，而某个字符是否存在只需要判断当前结点是否有表示这个字符的孩子节点即可，所以查询的速度非常快，也只有要查询的字符串的长度有关。

bool Trie::exist(const string& pKey)
{
    TrieNode *pNode = m_pRoot;
    for(size_t i = 0; i < pKey.length(); ++i)
    {
        char pAlpha = pKey.at(i);
        if(pNode->m_pNext[pAlpha - 97] != NULL)
        {
            pNode = pNode->m_pNext[pAlpha - 97];
        }
        else
        {
            return false;
        }
    }

    return true;
}

问题

由于每个节点的next数组不可能都有元素存在，而更可能的情况是每个节点的next数组的元素都比较少，造成了大量的空间浪费，要想解决这一问题，可以考虑用链表将孩子节点连接起来，但是在查询的过程中就会比较耗时。
另一种解决办法是采用双数组Trie树，仅用两个数组描述的字典树，同时可以处理各种字符，比较实用。

注：
图一来自于http://www.cnblogs.com/en-heng/p/6265256.html