LeetCode 236: 二叉树的最近公共祖先
二叉树的最近公共祖先
题目描述:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
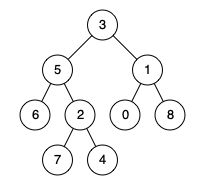
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2 输出:1
链接:
236. 二叉树的最近公共祖先 - 力扣(LeetCode) (leetcode-cn.com)
解题思路
思路一:递归解决
如果树为空树或p、q中任一节点为根节点,那么p、q的最近公共节点为根节点;如果不是,即二叉树不为空树,且p、q为非根节点,则递归遍历左右子树,获取左右子树的最近公共祖先:
- 如果p、q节点在左右子树的最近公共祖先都存在,说明p、q节点分布在左右子树的根节点上,此时二叉树的最近公共祖先为root;
- 若p、q节点在左子树最近公共祖先为空,那p、q节点位于左子树上,最终二叉树的最近公共祖先为右子树上p、q节点的最近公共祖先;
- 若p、q节点在右子树最近公共祖先为空,同左子树p、q节点的最近公共祖先为空一样的判定逻辑;
- 如果p、q节点在左右子树的最近公共祖先都为空,则返回null
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
if (root == null || root == p || root == q) return root;
const left = lowestCommonAncestor(root.left, p, q);
const right = lowestCommonAncestor(root.right, p, q);
if(left === null) return right;
if(right === null) return left;
return root;
};时间复杂度: O(n)
空间复杂度: O(n)
方法二:存储父节点
思路
我们可以用哈希表存储所有节点的父节点,然后我们就可以利用节点的父节点信息从 p 结点开始不断往上跳,并记录已经访问过的节点,再从 q 节点开始不断往上跳,如果碰到已经访问过的节点,那么这个节点就是我们要找的最近公共祖先。
算法:
从根节点开始遍历整棵二叉树,用哈希表记录每个节点的父节点指针。
从 p 节点开始不断往它的祖先移动,并用数据结构记录已经访问过的祖先节点。
同样,我们再从 q 节点开始不断往它的祖先移动,如果有祖先已经被访问过,即意味着这是 p 和 q 的深度最深的公共祖先,即 LCA 节点。
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function(root, p, q) {
let parent = new WeakMap;
let queue = [];
parent.set(root, null); //根节点没有父节点,所以为空
queue.push(root);
// 直到两个节点都找到为止
while (!parent.has(p) || !parent.has(q)) {
let node = queue.pop();
if (node.left != null) {
// 左子节点不为空,记录下他的父节点
parent.set(node.left, node);
// 左子节点不为空,把它加入到队列中
queue.push(node.left);
}
// 右节点同上
if (node.right != null) {
parent.set(node.right, node);
queue.push(node.right);
}
}
let set = new WeakSet;
//记录下p和他的祖先节点,从p节点开始一直到根节点。
while (p != null) {
set.add(p);
p = parent.get(p);
}
//查看p和他的祖先节点是否包含q节点,如果不包含再看是否包含q的父节点……
while (!set.has(q))
q = parent.get(q);
return q;
}时间复杂度: O(n)
空间复杂度: O(n);