广义回归神经网络(GRNN)的实现(Python,附源码及数据集)
文章目录
- 一、理论基础
-
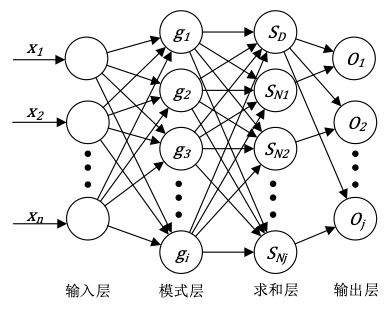
- 1、广义回归神经网络结构
- 2、输入层
- 3、模式层
- 4、求和层
- 5、输出层
- 6、优化思路
- 二、广义回归神经网络的实现
-
- 1、实现过程(GRNN.py)
- 2、预测结果
- 3、参考源码及实验数据集
一、理论基础
广义回归神经网络(Generalized Regression Neural Network,简称GRNN)是一种具有较好的非线性逼近能力的四层前向传播神经网络,它属于径向基神经网络的一种变形形式,数据输入网络后依次经过输入层、模式层、求和层、输出层后得到输出结果,与反向传播神经网络(BPNN)不通的是该网络没有训练过程,主要通过对模式层的平滑因子进行优化来获得好的输出结果。
反向传播神经网络(BPNN)原理参考:
反向传播神经网络(BPNN)的实现(Python,附源码及数据集)
1、广义回归神经网络结构
2、输入层
这一层主要实现数据的输入过程,并将输入数据传递至模式层,该层的节点数为输入数据的特征维度。
3、模式层
一般使用高斯函数对输入数据进行处理,节点数为训练样本的个数,具体的计算公式如下:
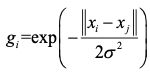
其中x_i为训练样本,x_j为学习样本,σ为平滑因子,
4、求和层
假设输出样本维度为k,则该层节点数为k+1,其中一个节点输出S_D为模式层输出的算术和,其余节点输出S_Ni均为模式层输出的加权和,具体的计算公式如下:


其中ω_ij为加权系数。
5、输出层
该层节点数为输出样本维度,主要根据求和层求出的算术和与加权和进行计算输出,计算公式如下:
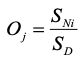
6、优化思路
虽然GRNN无需进行网络训练,但模式层的平滑因子σ对网络的性能影响较大,平滑因子过大或过小会分别导致网络出现欠拟合与过拟合的现象,而在实验中通常难以将平滑因子设定至较优的数值,因此若想获得较好的网络性能,一般选用高效的智能优化算法对平滑因子进行寻优。
常见的智能优化算法介绍
二、广义回归神经网络的实现
以数据预测为例,下面介绍基于Python实现径向基神经网络的过程。
选用某省市的表层土壤重金属元素数据集作为实验数据,该数据集总共96组,随机选择其中的24组作为测试数据集,72组作为训练数据集。选取重金属Ti的含量作为待预测的输出特征,选取重金属Co、Cr、Mg、Pb作为模型的输入特征。
1、实现过程(GRNN.py)
#库的导入
import numpy as np
import pandas as pd
#输入层
#读取训练数据
print('------------------------1. Load train data------------------------')
df = pd.read_csv("train.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
inputX = np.mat([Co,Cr,Mg,Pb])
inputX = inputX.transpose()
inputY = np.mat(Ti)
inputY = inputY.transpose()
#读取测试数据
print('------------------------2. Load test data-------------------------')
df = pd.read_csv("test.csv")
df = pd.read_csv("test.csv")
df.columns = ["Co", "Cr", "Mg", "Pb", "Ti"]
Co = df["Co"]
Co = np.array(Co)
Cr = df["Cr"]
Cr = np.array(Cr)
Mg=df["Mg"]
Mg=np.array(Mg)
Pb = df["Pb"]
Pb =np.array(Pb)
Ti = df["Ti"]
Ti = np.array(Ti)
testX = np.mat([Co,Cr,Mg,Pb])
testX = testX.transpose()
testY = Ti
#模式层
#计算样本欧式距离
print('----------------3. Calculate euclidean distance-------------------')
m, n = np.shape(inputX)
p = np.shape(testX)[0]
distance = np.mat(np.zeros((p, m)))
for i in range(p):
for j in range(m):
distance[i,j] = np.linalg.norm(testX[i,:]-inputX[j,:])
#计算高斯矩阵
print('------------------4. Calculate gaussian matrix--------------------')
sigma = 2 #平滑因子
Gauss = np.mat(np.zeros((p,m)))
for i in range(p):
for j in range(m):
Gauss[i,j] = np.exp(- distance[i,j] / (2 * (sigma ** 2)))
#求和层
print('----------------------5. Output of sum Layer----------------------')
n = np.shape(inputY)[1]
sum_mat = np.mat(np.zeros((p,n+1)))
#计算算术和
for i in range(p):
sum_mat[i, 0] = np.sum(Gauss[i, :], axis=1)
#计算加权和
for i in range(p):
for j in range(n):
total = 0.0
for s in range(m):
total += Gauss[i,s] * inputY[s,j]
sum_mat[i,j+1] = total
#输出层
print('--------------------6. Output of output Layer---------------------')
#计算预测值
predict = np.mat(np.zeros((p,n)))
for i in range(n):
predict[:,i] = sum_mat[:,i+1] / sum_mat[:,0]
predict = predict.transpose()
predict = np.array(predict)
output1=predict.flatten()#降成一维数组
predict=output1.tolist()
#预测效果评估
print('----------------7. Forecasting effect evaluation------------------')
#预测差值err
err = predict - testY
#MAE等评价指标的计算
mae = np.sum(np.abs(predict-testY))/p
average_loss1=np.sum(np.abs((predict-testY)/testY))/p
mape="%.2f%%"%(average_loss1*100)
f1 = 0
for m in range(p):
f1 = f1 + np.abs(testY[m]-predict[m])/((np.abs(testY[m])+np.abs(predict[m]))/2)
f2 = f1 / p
smape="%.2f%%"%(f2*100)
#计算预测值与真实值误差与真实值之比的分布
A=0
B=0
C=0
D=0
E=0
for m in range(p):
y1 = np.abs(testY[m]-predict[m])/np.abs(testY[m])
if y1 <= 0.1:
A = A + 1
elif y1 > 0.1 and y1 <= 0.2:
B = B + 1
elif y1 > 0.2 and y1 <= 0.3:
C = C + 1
elif y1 > 0.3 and y1 <= 0.4:
D = D + 1
else:
E = E + 1
print("The distribution of the predicted difference ratio in different intervals is as follows:")
print("Ratio <= 0.1 :",A)
print("0.1< Ratio <= 0.2 :",B)
print("0.2< Ratio <= 0.3 :",C)
print("0.3< Ratio <= 0.4 :",D)
print("Ratio > 0.4 :",E)
print("The different error index values are as follows:")
print("the MAE is :",mae)
print("the MAPE is :",mape)
print("the SMAPE is :",smape)
#保存误差和真实值
np.save("GRNN-err.npy",err)
np.save("GRNN-output.npy",predict)
print("The prediction value and real value comparison figure has been generated !")
2、预测结果

注:广义回归神经网络中参数主要是平滑因子,因此当设置不同取值的平滑因子时预测效果会存在一定差别。
3、参考源码及实验数据集
参考源码及实验数据集