神经网络（一）：GRNN广义回归神经网络理论概念笔记

GRNN广义回归神经网络以及相关概念

https://blog.csdn.net/zengxiantao1994/article/details/72787849
https://blog.csdn.net/guoyunlei/article/details/76101899参考博客
小小白入坑系列，欢迎大佬的指教!

算法网上铺天盖地的，我只是把自己对算法的理解和学习经验发到了这个帖子里面

把GRNN和RBF做一个对比，就会发现有以下区别：

1. 在实现上面，GRNN仅与RBF的输出层不同
2. 都对非线性数据具有很好的拟合效果
3. 在实际拟合过程中，数据比较优秀的时候，RBF的效果很好，不过在数据精准度比较差的时候，GRNN有很大优势，因为GRNN用的非参数估计进行后续的概率处理。

GRNN理论基础（汇总）

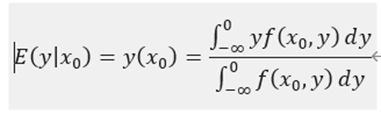
根据简单的概率论公式我们就能看懂上面的表达式，因为我们要用到parzan非参数估计，所以这里还是记录一下概率密度估计的一些内容（碎碎念，可以pass）

经典的参数估计：极大似然估计

这个是很多入手算法的朋友都会听过的概念，最经典的就是有一本书叫《概率机器人》里面有详细解读。

一切还是要从贝叶斯概率说起

后验概率 = (似然性*先验概率)/标准化常量。
这个式子告诉我们什么：我们在知道经验基础上可以推断出后续将要发生的事情的概率。

P(A):先验概率，表示每种类别分布的概率。
P（B|A）：类条件概率：表示某种类别前提下，某事发生的概率。

这个式子是很完美的，也产生很多不可避免的情况：
大多数时候下，不会有人告诉你P（A）和P（B|A）这两个数据的大小。
1.对与P（A），这个是很好搞定的，我们可以直接用样本进行估计就可以得到答案。
2.对与P(B|A)，这个就是一个很难啃的骨头，所以我们引出了极大似然估计

重要前提：训练样本的分布必须的能代表样本的真实分布

极大似然估计

就是很多时候，因为数据的误差存在，所以很多时候我们不能通过直接参数带入然后完成概率的估计，但是我们可以直接通过样本估计这个概率。
这里用到了求乘积最大，我理解就是乘积越大表示离真实概率越近，就好像最小二乘法那个R的估计一样，一个衡量指标，越大越好。

假设样本独立分布 D = {x1，x2…xn};

那么我们就设一个可以方便估计出P（A|B）的参数θ ， 要求通过θ求出P（A|B）。

这里，我们就设A=θ ，θ 知道了，根据贝叶斯公式，P（A）知道了，通过样本可以估计出P（B）（因为单独的样本都好估计），然后就差一个东西了，我们列出表达式：

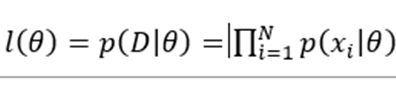
这里用θ ̂ 表示最大值

因为后续求出θ ̂ 的过程设计涉及求导，所以用ln函数来简化一下乘法求导的运算

然后对θ ̂ 直接求梯度 = 0就可以算出值了。
参数估计出来了就可以算出概率密度。

万事大吉了？

非参数估计的引入
传统的概率密度估计中，经典的概率密度函数都是单峰的，而且高维的一些概率密度也不一定和一维的运算关系差不多，所以上述的运算模型很有可能不适用，那么为了解决问题，数学家们引出了这个东西

parzen窗口估计和k临近估计

理论基础

概率密度的估计

设 向量x落在R内的概率如下

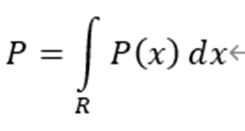
当R的提及很小时候，我们可以近似看成概率密度乘以体积

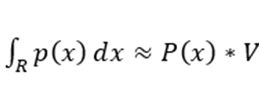
所以p（x） =P/V

设n个样本X1，X2…Xn,其中k个样本P（X） = Pk
Pk满足二项分布

所以 E（k） = nP ，因为已知k个样本了，所以E（k） = k
所以P = k\n;

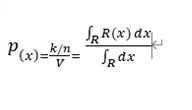
真实情况

上面我们其实做了很多假设，那么我们现在来实现这些假设用数学描述再进行理想化实现

第一个式子表示：体积足够小
第二个式子表示落入的k最够大，以代表概率密度
第三个表示样本容量足够大

那么我们需要实现这个等式，就要让这些等式成立，我们做这样的事情，分别对v和k进行操作。

所以就得到了两个算法
基本原理都是当概率为P（x）时候，容纳了k个样本的时，借此估计此时的概率密度

1.parzen窗估计

终于写到这里了。。
这里，我们定义R是以x为中心的超立方体，h为这个超立方体的边长，d是维度，V = h^d;
我们假设xi是第i个样本，那么我们这个样本落入超立方体的话，他就是1，没落入就是0

这个时候我们就可以看到落入到样本里面的k的数目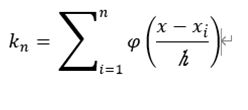
带入公式，就可以得到

这个就是窗的基本原理

2.kn临近估计

kn临近就是随着样本的增大，我们不断扩大体积，直到近似容纳k个样本为止，可以估算出此时的概率密度函数。

广义回归神经网络

回到正题，了解到parzen窗之后，我们把parzan窗的概率密度估算公式带入最初的式子

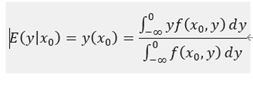
经过推导可以得出

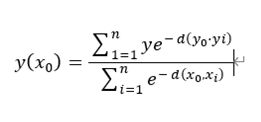
GRNN是需要
这个就是GRNN的理论基础辽，下篇敲matlab

不喜勿喷