TypeScript算法题实战——剑指 Offer篇(6)
目录
- 一、圆圈中最后剩下的数字
- 1.1、题目描述
- 1.2、题解
- 二、股票的最大利润
- 2.1、题目描述
- 2.2、题解
- 三、求1+2+…+n
- 3.1、题目描述
- 3.2、题解
- 四、不用加减乘除做加法
- 4.1、题目描述
- 4.2、题解
- 五、构建乘积数组
- 5.1、题目描述
- 5.2、题解
- 六、把字符串转换成整数
- 6.1、题目描述
- 6.2、题解
- 七、 二叉搜索树的最近公共祖先
- 7.1、题目描述
- 7.2、题解
- 八、二叉树的最近公共祖先
- 8.1、题目描述
- 8.2、题解
- 九、机器人的运动范围
- 9.1、题目描述
- 9.2、题解
- 十、H 指数
- 10.1、题目描述
- 10.2、题解
一支笔,一双手,一道力扣(Leetcode)做一宿!
在本文中,我们将使用TypeScript来解决剑指offer的算法题。这些问题涵盖了各种各样的主题,包括数组、字符串、链表、树、排序和搜索等。我们将使用TypeScript的强类型和面向对象的特性来解决这些问题,并通过实际的代码示例来演示如何使用TypeScript来解决算法问题。
题目全部来源于力扣题库:《剑指 Offer(第 2 版)》本章节包括的题目有(难度是我个人感受的难度,非官方标准):
| 题目 | 难度 |
|---|---|
| 圆圈中最后剩下的数字 | 困难 |
| 股票的最大利润 | 中等 |
| 求1+2+…+n | 中等 |
| 不用加减乘除做加法 | 困难 |
| 构建乘积数组 | 中等 |
| 把字符串转换成整数 | 中等 |
| 二叉搜索树的最近公共祖先 | 简单 |
| 二叉树的最近公共祖先 | 简单 |
| 机器人的运动范围 | 中等 |
| H 指数 | 简单 |
一、圆圈中最后剩下的数字
1.1、题目描述
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
输入: n = 5, m = 3
输出: 3
示例 2:
输入: n = 10, m = 17
输出: 2
1.2、题解
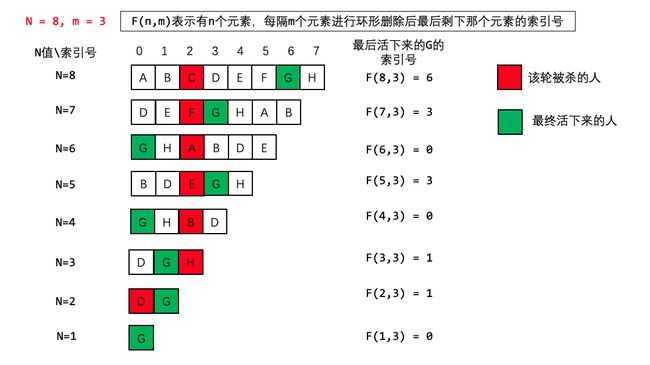
本题是著名的 “约瑟夫环” 问题,数字环是首尾相接的。
首先使用模拟法来想,首先建立一个长度为n的链表,每轮删除第m个节点,直至链表长度为1时结束,返回最后剩余的节点。但是模拟法要删除n-1轮,每轮要在链表中寻找需要m次,时间复杂度达到了O(n*m),明显会超时。
所以使用动态规划,全文最重要的点是只关心最终活着那个人的下标变化,设解为dp[i],dp[i]表示最后剩下来的数的当前下标
举个例子:
假设有一圈数字[0,1,2,3,4,5],m=3
我们令删除后的元素的后一个元素放在最前面方便计数
1.删除2->[3,4,5,0,1]
2.删除5->[0,1,3,4]
3.删除3->[4,0,1]
4.删除1->[4,0]
5.删除4->[0]
尝试反推:
如何从最后剩下的元素的索引0反推至第一轮元素索引呢?
注意到:2->1的过程是将删除的的元素5补在尾巴上变成[0,1,3,4,5],然后再总体向右移动m位
变成:[3,4,5,0,1];同样地,此时的最终活下来的元素0的索引由0->3
显然这是(idx+m)%len的结果,idx为删除5后的索引,len为补上删除元素后数组的长度
转移方程为:dp[i] = (dp[i - 1] + m)%i,代码其实很简单:
function lastRemaining(n: number, m: number): number {
let x = 0;
for(let i = 2; i <= n; i++)
x = (x + m) % i;
return x;
};
二、股票的最大利润
2.1、题目描述
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
2.2、题解
1️⃣:双指针算法
第一个指针保存当前遇见的最小投资点,第二个指针保存当前遇见的投资点,因为题目要求只能买卖一次,所以可边遍历边计算并保存当前最大期望收益。
一个指针记录访问过的最小值(注意这里是访问过的最小值),一个指针一直往后走,然后计算他们的差值,保存最大的即可,代码如下:
function maxProfit(prices: number[]): number {
if(prices.length == 0)
return 0;
let res = 0;
let min = prices[0];
for(let i = 1; i < prices.length; i++){
min = Math.min(min, prices[i]);
res = Math.max(prices[i] - min, res);
}
return res;
};
2️⃣:单调栈
单调栈解决的原理很简单,我们要始终保持栈顶元素是所访问过的元素中最小的,如果当前元素小于栈顶元素,就让栈顶元素出栈,让当前元素入栈。如果访问的元素大于栈顶元素,就要计算他和栈顶元素的差值,并记录这个差值的最大值。
其实这种方法与双指针法的原理相似,只不过保存时使用的栈来保存。
function maxProfit(prices: number[]): number {
if(prices.length == 0)
return 0;
let myStack = [];
myStack.push(prices[0]);
let max = 0;
for(let i = 1; i < prices.length; i++){
// 当前投资点小于之前的最佳投资点
// 即栈顶元素大于prices[i],那么栈顶元素出栈,
if(myStack[myStack.length - 1] > prices[i]){
myStack.pop();
myStack.push(prices[i]);
}else{
//栈顶元素不大于prices[i],计算prices[i]和栈顶元素的差值
max = Math.max(max, prices[i] - myStack[myStack.length - 1]);
}
}
return max;
};
3️⃣:动态规划
设动态规划列表 dp ,dp[i]代表以 prices[i]为结尾的子数组的最大利润,由于题目限定为“买卖股票一次”因此,前i日的最大利润dp[i] 等于Max(前i-1日的最大利润,第i日卖出的最大利润)
原理与前两个方法类似,只不过使用dp来保存之前的最大收益期望。
function maxProfit(prices: number[]): number {
if(prices.length < 2)
return 0;
let min = prices[0];
let dp:number[] = [0];
for(let i = 1; i < prices.length; i++){
min = Math.min(prices[i], min);
dp[i] = Math.max(dp[i - 1], prices[i] - min);
}
return dp[prices.length - 1]
};
三、求1+2+…+n
3.1、题目描述
求 1+2+…+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例 1:
输入: n = 3 输出: 6
示例 2:
输入: n = 9 输出: 45
3.2、题解
最简单就是使用递归解题:
function sumNums(n: number): number {
if(n == 0)
return 0;
return n + sumNums(n - 1);
};
由于题目不允许使用if关键字,所以我们使用&&运算符替换,当n大于0时都会运行后面(n += sumNums(n - 1),达到与上述代码同样的效果。
function sumNums(n: number): number {
return n && (n += sumNums(n - 1));
};
四、不用加减乘除做加法
4.1、题目描述
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
输入: a = 1, b = 1 输出: 2
4.2、题解
题目要求了不能使用运算符 +,-,*,/
所以我们考虑使用位运算来解决加法问题。
先从十进制来考虑加法原理,举个例子,15+17:
- 首先计算个位相加:5 + 7 = 12,个位为2,先不考虑进位问题
- 再计算十位相加:1 + 1 = 2, 十位为2
- 数字个十位相加,22
- 计算进位的数字:5 + 7 = 12,进位1,得到进位的数字有10
- 进位数与数字相加:10 + 22 = 32
从二进制的角度来讲,15的二进制为01111,17的二进制为10001
- 首先计算机各个位置上的数字分别相加: 01111 + 10001 = 1 1110
- 然后计算进位的数字,1 + 1 = 10
- 然后再计算11110 和 10 的相加,依次类推,直至后面这个数即b为0;
在位运算中,第一步可以用异或来做,即^
而计算进位的数字可以用与和左移来算,如01 & 01 = 01,然后左移即可得到进位10
function add(a: number, b: number): number {
if(b == 0)
return a;
let currN = a ^ b;
let upN = (a & b) << 1;
return add(currN, upN);
};
五、构建乘积数组
5.1、题目描述
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1],不能使用除法。
示例:
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]
5.2、题解
首先想到的是用总乘积除以当前数,但是不能用除法,而且数组中间存在0,如果除0会出现问题。
而如果用暴力来模拟:
function constructArr(a: number[]): number[] {
let res: number[] = [];
for(let i = 0; i < a.length; i++){
let temp = 1;
for(let j = 0; j < a.length; j++){
if(j == i)
continue;
temp = temp * a[j];
}
res.push(temp);
}
return res;
};
时间复杂度 O ( N 2 ) O(N^2) O(N2),会超时:
这里采用左右乘积列表方法,即构建一个左列表存储索引左侧所有数字的乘积,构建一个右列表存储索引左侧所有数字的乘积,对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。
function constructArr(a: number[]): number[] {
let left = [1];
let right = [];
let res = [];
for(let i = 1; i < a.length; i++){
left[i] = a[i - 1] * left[i - 1];
}
right[a.length - 1] = 1;
for(let i = a.length - 2; i >= 0; i--){
right[i] = a[i + 1] * right[i + 1];
}
for(let i = 0; i < a.length; i++){
res[i] = left[i] * right[i];
}
return res;
};
六、把字符串转换成整数
6.1、题目描述
写一个函数 StrToInt,实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
示例 1:
输入: “42” 输出: 42
示例 2:
输入: " -42" 输出: -42
解释: 第一个非空白字符为 ‘-’, 它是一个负号。
示例 3:
输入: “4193 with words” 输出: 4193
解释: 转换截止于数字 ‘3’ ,因为它的下一个字符不为数字。
示例 4:
输入: “words and 987” 输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。因此无法执行有效的转换。
示例 5:
输入: “-91283472332” 输出: -2147483648
解释: 数字 “-91283472332” 超过 32位有符号整数范围。 因此返回 INT_MIN (−231) 。
6.2、题解
这里补充正则表达式用到的RegExp对象的match方法:match()方法是RegExp对象的一个方法,用来检索字符串中符合正则表达式规则的字符串,并将匹配到的字符串以数组形式返回,用法如下:
let regExp = new RegExp('/^[-+]?(\d+)/');
let res = str.match(regExp);
这里我们使用:正则表达式处理,提取后比较范围然后判断:
function strToInt(str: string): number {
str = str.trim(); // 去掉前后空格
let INT_MIN = -Math.pow(2,31), INT_MAX = Math.pow(2,31) - 1;
let regExp = new RegExp(/^[\+\-]?\d+/);
let res = str.match(regExp);
console.log(res);
if(res == null)
return 0;
if(res[0][0] == '-' && Number(res[0]) < INT_MIN){
return INT_MIN;
}
if(Number(res[0]) > INT_MAX){
return INT_MAX;
}
return Number(res[0]);
};
图简单的方法,这里可以使用parseInt() 函数,parseInt() 函数可解析一个字符串,并返回一个整数,parseInt() 函数可以处理以下情况:
- 解析正整数:当字符串以数字开头时,parseInt() 将从字符串的开头开始解析直到遇到非数字字符。它会忽略字符串开头的空白字符,并返回解析后的整数。
- 解析负整数:当字符串以负号(-)开头时,parseInt() 会将其视为一个负整数。
- 处理非数字字符:当字符串中包含非数字字符时,parseInt() 将停止解析,并返回已解析的部分。例如,parseInt(“123abc”) 将返回 123。
- 处理基数(进制):通过提供第二个参数 radix,可以指定解析时所使用的基数。例如,parseInt(“10”, 2) 将按二进制解析字符串 “10”,返回 2。
- 忽略浮点数部分:parseInt() 函数将忽略字符串中的小数点和小数部分。例如,parseInt(“3.14”) 将返回 3。
- parseInt() 函数还有一些特殊情况,例如在解析以 0x 开头的字符串时会将其视为十六进制数
这里可以直接调用函数,然后判断一下最大和最小范围:
function strToInt(str: string): number {
let m = Math.pow(2, 31);
return Math.min(Math.max(parseInt(str) || 0, -m), m - 1);
};
七、 二叉搜索树的最近公共祖先
7.1、题目描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
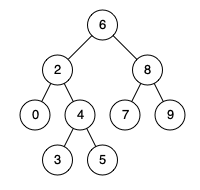
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释:节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身
7.2、题解
使用递归法,从根节点找起,显然可得最近公共祖先的值肯定是大于其中一个数,小于另外一个数,使用递归法,如果当前节点同时大于这两个数,则他两肯定在左子树当中,如果当前节点同时小于这两个数,则他两肯定在右子树当中,如此查找,直到第一次出现一个在左子树,一个在右子树则满足条件:
function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
if(root.val > p.val && root.val > q.val){
return lowestCommonAncestor(root.left, p, q);
}
if(root.val < p.val && root.val < q.val){
return lowestCommonAncestor(root.right, p, q);
}
return root;
};
八、二叉树的最近公共祖先
8.1、题目描述
这一题题干跟前一题类似,唯一的不同是这里的二叉树是普通二叉树,不再是二叉搜索树
8.2、题解
同样采用递归的方法,但此时需要判断左子树是否存在p或q中的一个,判断右子树是否存在p或q中的一个,如果左子树存在一个,右子树存在一个则返回当前节点,若只有左子树存在(右边找的为空),则访问左子树,若只有右子树存在(左边找的为空),则访问右子树。
function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
if(root == null)
return null;
if(root == p || root == q)
return root;
let left = lowestCommonAncestor(root.left, p, q);
let right = lowestCommonAncestor(root.right, p, q);
// 即在第一次该节点的左子树和右子树上分别找到了p 和 q
if(left !== null && right !== null){
return root;
}
// 暂时只找到一个
else if(left == null){
return right;
}
else if(right == null){
return left;
}
};
九、机器人的运动范围
9.1、题目描述
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
9.2、题解
首要要理解一下题目,题目说的是数位之和不大于k,即比如[13,12],数位之和为1+3+1+2=7,所以m = 2, n = 3, k = 1时,满足条件的有[0,0],[0,1],[1,0]三个结果
m = 3, n = 1, k = 0时,满足条件的有[0,0]一个结果。
设立res作为全局结果数量,visited数组记录是否已经被访问过,然后使用采用dfs方法遍历所有情况:
function movingCount(m: number, n: number, k: number): number {
let res = 0;
let visited = new Array(m).fill(0).map(()=> new Array(n).fill(false));
function dfs(i:number, j:number){
if(sum(i, j) > k || i < 0 || j < 0 || i >= m || j >= n || visited[i][j])
return;
res ++;
visited[i][j] = true;
dfs(i, j + 1);
dfs(i, j - 1);
dfs(i - 1, j);
dfs(i + 1, j);
}
function sum(i:number, j:number):number{
return Math.floor(i / 10) + i % 10 + Math.floor(j / 10) + j % 10
}
dfs(0, 0);
return res;
};
十、H 指数
10.1、题目描述
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且每篇论文 至少 被引用 h 次。如果 h 有多种可能的值,h 指数 是其中最大的那个。
10.2、题解
先从小到大排序,然后从后往前遍历,将h因子置为0,从影响因子最大的文章开始,当citations[i] > h时,h++:
function hIndex(citations: number[]): number {
citations.sort(function(a,b){return a-b});
let h = 0;
for(let i = citations.length - 1; i >= 0; i--){
if(citations[i] > h){
h++;
}
}
return h;
};