C++之红黑树剖析
博主：拖拉机厂第一代码手
gitee:拖拉机厂第一代码手
已收录到专栏C++，点击访问
目录
- 红黑树简介
- 红黑树的插入操作
- 红黑树的删除操作
- 红黑树的实现
-
- 红黑树节点的定义
- 红黑树结构的定义
- 红黑树的插入实现
- 红黑树的删除实现
- 红黑树插入和删除测试
- 总结
红黑树简介
红黑树是一种自平衡的二叉搜索树，它是由 Rudolf Bayer 在1972年提出，并由 Leonidas J. Guibas 和 Robert Sedgewick 在1978年进行改进和推广的。红黑树是一种复杂的数据结构，旨在确保在最坏情况下的高效的插入、删除和查找操作。
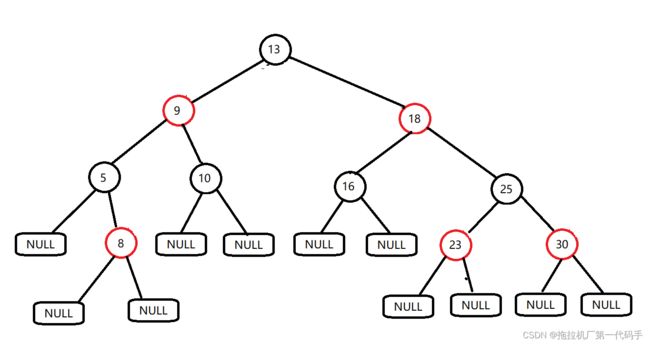
红黑树之所以被称为红黑树，是因为每个节点有一个存储的二进制值来表示节点的颜色，通常为红色或黑色。除了满足二叉搜索树的特性之外，红黑树还满足以下额外特性：
- 每个节点要么是红色，要么是黑色。
- 根节点是黑色。
- 每个叶子节点（NIL节点，空节点）是黑色。
- 如果一个节点是红色的，则它的两个子节点都是黑色的。
- 对于每个节点，从该节点到其后代的每个叶子节点的简单路径上，黑色节点的数量相同。
这些特性确保了红黑树的平衡性，使得在最坏情况下，红黑树的插入、删除和查找操作的时间复杂度都是 O(log n)，其中 n 是树中节点的数量。
由于红黑树具有自平衡的特性，所以它在各种应用中得到广泛应用，例如在操作系统中的进程调度、文件系统的实现，以及在数据结构库中用于提供高效的数据结构支持等。
红黑树通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。（ps：因为在满足红黑树条件的情况下，该树的最长路径为红黑相间的路径，而最短的路径为全黑的路径）
红黑树的插入操作
红黑树是一种自平衡的二叉搜索树，它在插入操作时通过对节点进行着色和旋转操作来保持平衡。下面是红黑树插入新节点的过程：
- 将新节点插入二叉搜索树中，按照二叉搜索树的插入规则进行。
- 将新节点着色为红色。这是为了保护红黑树的性质，后续操作中会逐步调整节点的颜色。
- 根据红黑树的性质进行调整，有以下几种情况需要考虑：
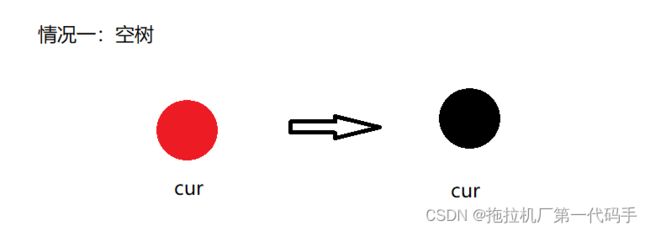
a. 新节点是根节点：将新节点着色为黑色，以确保性质2（根节点为黑色）被满足。
b. 新节点的父节点是黑色：由于新节点是红色，所以红黑树的性质没有被破坏。不需要做任何额外的调整。
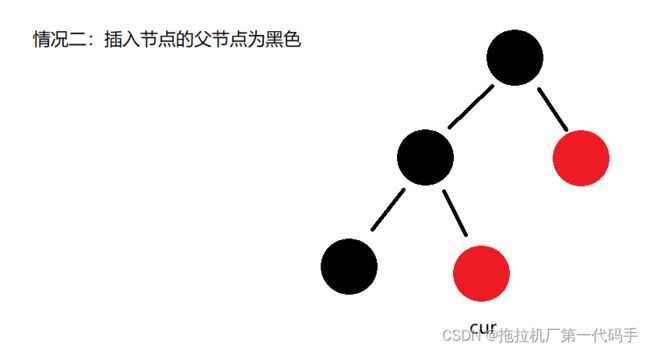
c. 新节点的父节点是红色：
- 新节点的叔叔节点是红色：通过修改颜色调整，将父节点和叔叔节点着色为黑色，父节点的父节点（祖父节点）着色为红色，然后以祖父节点为当前节点递归进行调整。
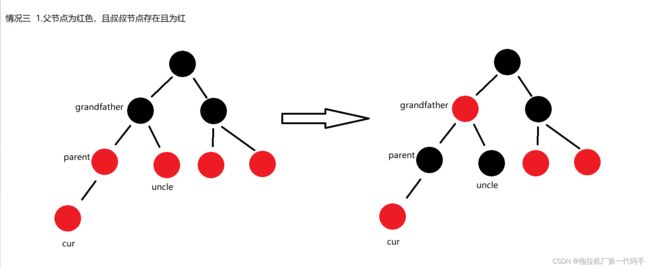
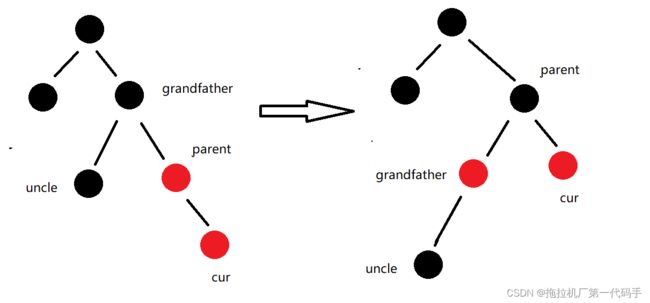
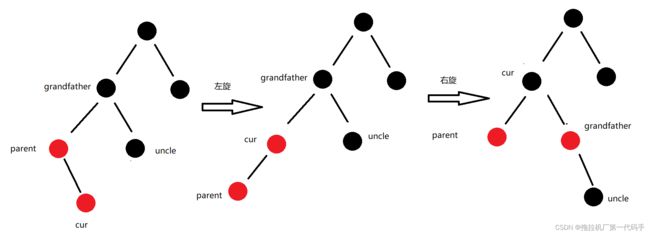
- 新节点的叔叔节点是黑色或者不存在：通过旋转和颜色调整实现平衡。具体操作分为四种情况：
- 新节点是父节点的左子节点，并且父节点是祖父节点的左子节点：进行右旋操作，并交换父节点和祖父节点的颜色。
- 新节点是父节点的右子节点，并且父节点是祖父节点的右子节点：进行左旋操作，并交换父节点和祖父节点的颜色。
- 新节点是父节点的右子节点，并且父节点是祖父节点的左子节点：进行左旋操作，然后进行右旋操作，并交换新节点和祖父节点的颜色。
- 新节点是父节点的左子节点，并且父节点是祖父节点的右子节点：进行右旋操作，然后进行左旋操作，并交换新节点和祖父节点的颜色。
说明：cur的情况有两种
- 如果cur节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点，则cur和p一定有一个节点的颜色是黑色，就不满足性质4：每条路径黑色节点个数相同。
- 如果u节点存在，则其一定是黑色的，那么cur节点原来的颜色也一定是黑色的，现在看到具是红色的原因是因为cur的子树在调整的过程中将cu市点的颜色由黑色改成红色。
- 将根节点着色为黑色，以满足性质2。
以上就是红黑树插入操作的过程。通过这些调整，红黑树始终保持平衡，并满足红黑树的五个性质。这些操作保证了红黑树插入的时间复杂度为O(logn)。
红黑树的删除操作
红黑树的删除操作相较于插入操作要复杂一些。下面是红黑树删除节点的详细过程：
首先，按照二叉搜索树的规则找到需要删除的节点，并标记为要删除的节点。
判断要删除的节点是否有子节点：
a. 若没有子节点，则直接删除该节点，并将其父节点指向它的指针置为null。
b. 若只有一个子节点，将其子节点代替要删除的节点的位置，并更新子节点的父节点指针。
c. 若有两个子节点，需要找到要删除节点的后继节点（右子树最小值节点）或者前驱节点（左子树最大值节点），将后继节点（或前驱节点）的值复制到要删除的节点中，并将要删除的节点指向后继节点（或前驱节点），然后将要删除的节点更新为后继节点（或前驱节点）。
接下来需要处理删除后的情况，根据被删除节点的性质以及其子节点的颜色进行相应的调整，有以下几种情况：
- a. 被删除节点为红色节点：
由于红色节点的删除不会破坏红黑树的性质，所以直接删除即可，无需其他调整。
- b. 被删除节点为黑色节点：
被删除节点的子节点为红色节点：将子节点改为黑色，以保持红黑树的性质。这种情况下，被删除节点是根节点的话，只需要将子节点改为黑色即可。
被删除节点的子节点为黑色节点：
- （1）被删除节点为根节点：无需额外处理；
- （2）被删除节点的兄弟节点为红色节点：进行旋转和颜色调整，使被删除节点的兄弟节点变为黑色节点，然后继续处理；
- （3）被删除节点的兄弟节点为黑色节点：
- i. 如果兄弟节点的两个子节点都为黑色：将兄弟节点改为红色，将被删除节点的父节点作为新的被删除节点进行递归调整。
- ii. 如果兄弟节点左子节点为红色，右子节点为黑色：进行旋转和颜色调整，使兄弟节点的左子节点变为黑色，兄弟节点变为红色，并对兄弟节点进行右旋操作；
- iii. 如果兄弟节点右子节点为红色：进行旋转和颜色调整，将兄弟节点的颜色设置为被删除节点父节点的颜色，被删除节点的父节点设置为黑色，兄弟节点的右子节点设置为黑色，然后对被删除节点的父节点进行左旋操作。
将根节点设置为黑色，以满足红黑树的性质2。
通过上述步骤，可以在删除节点后重新调整红黑树，以保持平衡并满足红黑树的所有性质。这些操作确保了红黑树删除操作的时间复杂度为O(logn)。
红黑树的实现
红黑树节点的定义
// 定义红黑树节点
template <typename Key, typename Value>
struct RBTreeNode
{
enum Color { RED, BLACK };
Key key; // 节点的键值
Value value; // 节点的值
RBTreeNode* left; // 左子节点指针
RBTreeNode* right; // 右子节点指针
RBTreeNode* parent; // 父节点指针
Color color; // 节点的颜色
// 构造函数
RBTreeNode(Key k, Value v, Color c = RED)
: key(k), value(v), left(nullptr), right(nullptr), parent(nullptr), color(c) {}
};
在以上的代码中，每个红黑树节点包含以下属性：
- key：节点的键值，用于对节点进行排序。
- value：节点的值，可以是任意类型的数据。
- left：指向左子节点的指针。
- right：指向右子节点的指针。
- parent：指向父节点的指针，根节点的父节点为空。
- color：指示节点的颜色，默认为红色。使用枚举类型 Color 表示节点的颜色，包括红色（RED）和黑色（BLACK）。
这是一个简单的红黑树节点的定义示例，可以根据具体需求进行适当修改和扩展。
红黑树结构的定义
// 定义红黑树结构
template <typename Key, typename Value>
struct RBTree
{
RBTreeNode<Key, Value>* header; // 头结点
// 构造函数
RBTree()
{
header = new RBTreeNode<Key, Value>(Key(), Value(), RBTreeNode<Key, Value>::BLACK);
header->left = header;
header->right = header;
header->parent = nullptr;
}
};
在以上的代码中，我们在红黑树结构中添加了一个头结点（哨兵节点），用于表示红黑树的边界。头结点的key和value值可以设为默认值，而且颜色为黑色（BLACK）以满足红黑树性质。
通过添加头结点，我们可以很方便地访问红黑树的最小节点和最大节点，可以使用 header->left 来访问最小节点，使用 header->right 来访问最大节点。
这种修改可以方便地实现关联式容器，并在插入、删除操作时简化边界条件的处理。
红黑树的插入实现
// 红黑树的插入操作
template<typename Key, typename Value>
void RBTree<Key, Value>::insert(Key key, Value value) {
RBTreeNode<Key, Value>* newNode = new RBTreeNode<Key, Value>(key, value);
RBTreeNode<Key, Value>* parent = nullptr;
RBTreeNode<Key, Value>* current = header->parent;
// 找到插入位置
while (current != nullptr) {
parent = current;
if (key < current->key)
current = current->left;
else if (key > current->key)
current = current->right;
else {
// 如果已存在相同的键值，则更新节点的值
current->value = value;
delete newNode;
return;
}
}
newNode->parent = parent;
// 空树，插入为根节点
if (parent == nullptr) {
newNode->color = RBTreeNode<Key, Value>::BLACK;
header->parent = newNode;
header->left = newNode;
header->right = newNode;
}
else if (key < parent->key)
parent->left = newNode;
else
parent->right = newNode;
// 插入后进行调整
insertFixup(newNode);
}
// 红黑树插入后的调整操作
template <typename Key, typename Value>
void RBTree<Key, Value>::insertFixup(RBTreeNode<Key, Value>* node) {
while (node->parent != nullptr && node->parent->color == RBTreeNode<Key, Value>::RED) {
if (node->parent == node->parent->parent->left) {
RBTreeNode<Key, Value>* uncle = node->parent->parent->right;
if (uncle != nullptr && uncle->color == RBTreeNode<Key, Value>::RED) {
// Case 1: 叔叔节点是红色
node->parent->color = RBTreeNode<Key, Value>::BLACK;
uncle->color = RBTreeNode<Key, Value>::BLACK;
node->parent->parent->color = RBTreeNode<Key, Value>::RED;
node = node->parent->parent;
}
else {
if (node == node->parent->right) {
// Case 2: 插入节点是父节点的右子节点
node = node->parent;
rotateLeft(node);
}
// Case 3: 插入节点是父节点的左子节点
node->parent->color = RBTreeNode<Key, Value>::BLACK;
node->parent->parent->color = RBTreeNode<Key, Value>::RED;
rotateRight(node->parent->parent);
}
}
else {
// 与上述情况对称
RBTreeNode<Key, Value>* uncle = node->parent->parent->left;
if (uncle != nullptr && uncle->color == RBTreeNode<Key, Value>::RED) {
node->parent->color = RBTreeNode<Key, Value>::BLACK;
uncle->color = RBTreeNode<Key, Value>::BLACK;
node->parent->parent->color = RBTreeNode<Key, Value>::RED;
node = node->parent->parent;
}
else {
if (node == node->parent->left) {
node = node->parent;
rotateRight(node);
}
node->parent->color = RBTreeNode<Key, Value>::BLACK;
node->parent->parent->color = RBTreeNode<Key, Value>::RED;
rotateLeft(node->parent->parent);
}
}
}
header->parent->color = RBTreeNode<Key, Value>::BLACK; // 根节点始终为黑色
}
以上代码是一个红黑树的实现，包括插入操作insert()、插入修复操作insertFixup()，以及左旋和右旋操作rotateLeft()和rotateRight()。
在插入操作中，首先创建一个新的节点，并根据键的大小将其插入到适当的位置。如果已存在相同的键值，则会更新节点的值。然后，根据插入的节点进行插入修复操作insertFixup()，以恢复红黑树的性质。
插入修复操作insertFixup()是用来保持红黑树的性质。它根据插入节点的父节点、祖父节点和叔叔节点的颜色进行不同的操作。具体来说，如果叔叔节点是红色（Case 1），则通过改变颜色来修复；如果插入节点是父节点的右子节点（Case 2），则进行左旋操作；如果插入节点是父节点的左子节点（Case 3），则进行右旋操作。
左旋操作rotateLeft()将某个节点的右子节点上移，同时该节点成为其右子节点的左子节点。右旋操作rotateRight()将某个节点的左子节点上移，同时该节点成为其左子节点的右子节点。这些操作用于调整红黑树的平衡。
总的来说，这些代码实现了红黑树的插入操作和相应的修复操作，以及左旋和右旋操作。这些是保持红黑树性质的重要操作。
红黑树的删除实现
// 红黑树的删除操作
template<typename Key, typename Value>
void RBTree<Key, Value>::remove(Key key) {
RBTreeNode<Key, Value>* node = findNode(key);
if (node == nullptr)
return;
RBTreeNode<Key, Value>* child;
RBTreeNode<Key, Value>* parent;
bool isRed = (node->color == RBTreeNode<Key, Value>::RED);
if (node->left != nullptr && node->right != nullptr) {
// Case 1: 被删除节点有两个子节点
RBTreeNode<Key, Value>* replace = node->right;
while (replace->left != nullptr)
replace = replace->left;
child = replace->right;
parent = replace->parent;
isRed = (replace->color == RBTreeNode<Key, Value>::RED);
if (child != nullptr)
child->parent = parent;
if (parent != nullptr) {
if (parent->left == replace)
parent->left = child;
else
parent->right = child;
}
else {
header->parent = child;
}
if (replace->parent == node)
parent = replace;
replace->parent = node->parent;
replace->color = node->color;
replace->left = node->left;
replace->right = node->right;
if (node->left != nullptr)
node->left->parent = replace;
if (node->right != nullptr)
node->right->parent = replace;
if (node->parent != nullptr) {
if (node->parent->left == node)
node->parent->left = replace;
else
node->parent->right = replace;
}
else {
header->parent = replace;
}
delete node;
node = replace;
}
else {
// Case 2: 被删除节点无或只有一个子节点
if (node->left != nullptr)
child = node->left;
else
child = node->right;
parent = node->parent;
isRed = (node->color == RBTreeNode<Key, Value>::RED);
if (child != nullptr)
child->parent = parent;
if (parent != nullptr) {
if (parent->left == node)
parent->left = child;
else
parent->right = child;
}
else {
header->parent = child;
}
delete node;
}
if (!isRed) {
// 删除后进行调整
removeFixup(child, parent);
}
}
// 红黑树删除后的调整操作
template <typename Key, typename Value>
void RBTree<Key, Value>::removeFixup(RBTreeNode<Key, Value>* node, RBTreeNode<Key, Value>* parent) {
while (node != header->parent && (node == nullptr || node->color == RBTreeNode<Key, Value>::BLACK)) {
if (node == parent->left) {
RBTreeNode<Key, Value>* sibling = parent->right;
if (sibling->color == RBTreeNode<Key, Value>::RED) {
// Case 1: 兄弟节点是红色
sibling->color = RBTreeNode<Key, Value>::BLACK;
parent->color = RBTreeNode<Key, Value>::RED;
rotateLeft(parent);
sibling = parent->right;
}
if ((sibling->left == nullptr || sibling->left->color == RBTreeNode<Key, Value>::BLACK)
&& (sibling->right == nullptr || sibling->right->color == RBTreeNode<Key, Value>::BLACK)) {
// Case 2: 兄弟节点和兄弟节点的子节点都是黑色
sibling->color = RBTreeNode<Key, Value>::RED;
node = parent;
parent = node->parent;
}
else {
if (sibling->right == nullptr || sibling->right->color == RBTreeNode<Key, Value>::BLACK) {
// Case 3: 兄弟节点的右子节点是黑色
if (sibling->left != nullptr)
sibling->left->color = RBTreeNode<Key, Value>::BLACK;
sibling->color = RBTreeNode<Key, Value>::RED;
rotateRight(sibling);
sibling = parent->right;
}
// Case 4: 兄弟节点的右子节点是红色
sibling->color = parent->color;
parent->color = RBTreeNode<Key, Value>::BLACK;
if (sibling->right != nullptr)
sibling->right->color = RBTreeNode<Key, Value>::BLACK;
rotateLeft(parent);
node = header->parent;
break;
}
}
else {
// 与上述情况对称
RBTreeNode<Key, Value>* sibling = parent->left;
if (sibling->color == RBTreeNode<Key, Value>::RED) {
sibling->color = RBTreeNode<Key, Value>::BLACK;
parent->color = RBTreeNode<Key, Value>::RED;
rotateRight(parent);
sibling = parent->left;
}
if ((sibling->left == nullptr || sibling->left->color == RBTreeNode<Key, Value>::BLACK)
&& (sibling->right == nullptr || sibling->right->color == RBTreeNode<Key, Value>::BLACK)) {
sibling->color = RBTreeNode<Key, Value>::RED;
node = parent;
parent = node->parent;
}
else {
if (sibling->left == nullptr || sibling->left->color == RBTreeNode<Key, Value>::BLACK) {
if (sibling->right != nullptr)
sibling->right->color = RBTreeNode<Key, Value>::BLACK;
sibling->color = RBTreeNode<Key, Value>::RED;
rotateLeft(sibling);
sibling = parent->left;
}
sibling->color = parent->color;
parent->color = RBTreeNode<Key, Value>::BLACK;
if (sibling->left != nullptr)
sibling->left->color = RBTreeNode<Key, Value>::BLACK;
rotateRight(parent);
node = header->parent;
break;
}
}
}
if (node != nullptr)
node->color = RBTreeNode<Key, Value>::BLACK;
}
这段代码是红黑树的删除操作和删除修复操作的实现。
在删除操作中，首先找到要删除的节点，如果节点不存在则直接返回。然后根据节点的情况进行处理：
- Case 1: 当被删除节点有两个子节点时，找到后继节点（右子树的最左节点），并用后继节点替换被删除节点。
- Case 2: 当被删除节点只有一个子节点或者没有子节点时，直接用子节点来替换被删除节点。
然后，检查被删除节点的颜色，如果是红色则不需要进行调整，直接删除即可。如果是黑色，则需要进行删除修复操作removeFixup()，以确保红黑树的性质。删除修复操作分为四种情况，根据被删除节点的兄弟节点的颜色和子节点的颜色来进行相应的旋转操作和颜色调整，最终保持红黑树的性质。
在实现中，调用了左旋rotateLeft()和右旋rotateRight()操作来进行树的旋转调整。
红黑树插入和删除测试
int main() {
RBTree<int, std::string> tree;
// 插入测试
tree.insert(10, "Value 10");
tree.insert(5, "Value 5");
tree.insert(15, "Value 15");
tree.insert(3, "Value 3");
tree.insert(8, "Value 8");
tree.insert(12, "Value 12");
tree.insert(18, "Value 18");
tree.insert(2, "Value 2");
tree.insert(4, "Value 4");
tree.insert(7, "Value 7");
tree.insert(9, "Value 9");
tree.insert(11, "Value 11");
tree.insert(14, "Value 14");
tree.insert(17, "Value 17");
tree.insert(20, "Value 20");
// 遍历测试
std::cout << "begin In-order traversal:\n";
tree.inOrderTraversal();
// 删除测试
tree.remove(9);
tree.remove(12);
tree.remove(18);
// 遍历测试
std::cout << "end In-order traversal:\n";
tree.inOrderTraversal();
return 0;
}
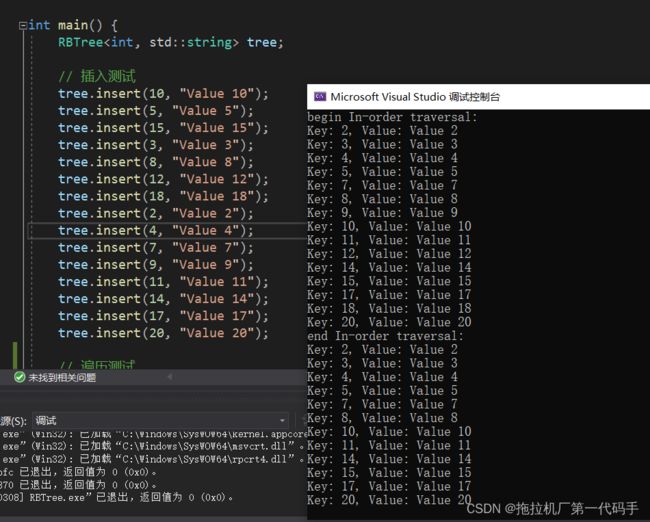
这段代码创建了一个整型键和字符串值的红黑树。首先，通过insert()函数插入了一系列键值对，然后通过inOrderTraversal()函数进行中序遍历，输出红黑树的节点信息。接着，通过remove()函数进行删除操作，删除了键为9、12和18的节点。最后，再次进行中序遍历测试，输出删除后的红黑树节点信息。
总结
文章对红黑树的特性进行了详细介绍，对红黑树的插入和删除的具体步骤进行分析并用代码实现出来，完整代码放到了gitee仓库，有需要自取。
最后，如果觉得文章对你有帮助的话，就来一个小小的吧。
