二叉树遍历的非递归实现（C语言）

内容:

   编写程序，实现下述功能，并上机调试通过

   (1)按中序顺序建立一棵二叉树；

   (2)用非递归方式遍历二叉树（先序），输出遍历序列。

【提示】采用二叉链表做存储结构，建立二叉树。借助于栈结构来实现二叉树遍历的非递归算法。

步骤：

1.算法分析：

       根据题目需求，可知整个程序需要两个比较大的板块，第一个是要根据中序顺序建立一个二叉树，第二个是最重要的也是核心的是用非递归先序方式遍历二叉树。

       首先来看第一步，要想完成第一步，首先需要了解到无论是扩展二叉树亦或是其他普通的二叉树只单靠一个中序顺序是不能建立起一个二叉树的，若不扩展二叉树则至少需要前序+中序或者中序+后序才能完成一个二叉树的建立。主要是因为只有一个中序顺序是无法知道根结点的，所以无法完成对根节点的定位。而先序扩展二叉树，其根节点就是首位，而且其空余位置已被填充，只需要根据二叉树的每行有2^(i-1)个结点依次填充即可推断出整个二叉树。所以就算有中序扩展二叉树的遍历结果，也不行。所以主要是借助于二叉树的遍历结果对整个二叉树进行恢复，但是还不如就直接用扩展二叉树。因为要对二叉树进行恢复远比直接输入一个扩展二叉树复杂。

       利用扩展二叉树的遍历结果恢复二叉树代码如下：

void CreateBiTree(BiTree *T)
{
	char ch;
	ch=getchar();
	if(ch=='#')(*T)=NULL;   //#代表空指针
	   else
	   {
	   	    (*T)=(BiTree)malloc(sizeof(BiTNode));  //申请结点
			(*T)->data=ch;                         //生成根节点
			CreateBitree(&(*T)->lchild);           //构造左子树
			CreateBitree(&(*T)->rchild);           //构造右子树 
		} 
 }

        其中利用中序和先序的结果恢复的遍历代码如下：

void ReBiTree(char preod[],char inod[],int a,BiTree root)
{//n为二叉树的结点个数，root为二叉树根节点的存储地址
	if(n<=0)
	  root=NULL;
	else
	  PreInOd(preod,indod,1,n,1,n,&root);
}
void PreInOd(char preod[],char inod[],int i,int j,int k,int h,BiTree *t)
{//以先序序列preod[i…j],中序序列inod[k…h]恢复二叉树
	*t=(BiTNode *)malloc(sizeof(BiTNode));
	*t->data=preod[i];
	m=k;
	while(inod[m]!=preod[i])
	   m++;      //在inod[]中查找preod[i]
	if(m==k)
	   *t->lchild=NULL
	else
	   PreInOd(preod,inod,i+1,i+m-k,k,m-1,&t->lchild);
//以先序序列preod[i+1...i+m-k],中序序列inod[k…m-1]恢复二叉树&t->lchild
	if(m==h)
	   *t->rchild=NULL
	else
	   PreInOd(preod,inod,i+m-k+1,j,m+1,h,&t->rchild); 
//以先序序列preod[i+m-k+1…j]，中序序列inod[m+1…h]恢复二叉树&->rchild
}

       第二个部分为非递归先序遍历的实现，遍历二叉树的路线正是从根节点开始沿左子树深入下去，当深入到最左端，无法再深入下去时，则返回，再逐一进入刚才深入时遇到的结点和左子树，再进行如此的深入和返回，直到最后从根节点的右子树返回到根节点为止。先序遍历是在深入时遇到结点就访问。在这一过程中，返回结点的顺序与深入结点的顺序相反，即后深入先返回，正好符合栈结构的后进先出的特点。过程如下：在沿左子树深入时，深入一个结点入栈一个结点，先序遍历，在入栈之前访问，当沿左分支深入过程中遇到空分支，则返回，即从堆栈中弹出前面压入的结点。

       其实，非递归过程很简单。就是遇到结点就深入，若该节点有孩子就将该节点入栈，之后继续深入。在判空的时候返回上一结点并访问。然后访问该结点的右孩子，之后返回判空。若为真，则将该结点退栈，不打印。非递归的程序主要是使用两个while语句的嵌套完成。外层嵌套的while语句主要负责判断指针p指向的下一结点是否为空以及栈中元素是否全部完成退栈操作，内层while语句主要负责将指针p压栈，以及访问结点的左右孩子。下面用一个简单的例子还原一下非递归的过程。

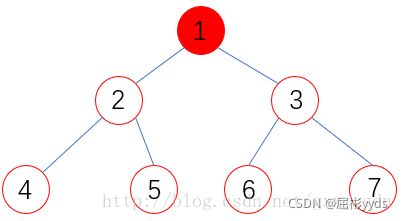
1. 进入第一层whil判断语句，并将1压入栈中，指针指向1的左孩子。此时栈为1，2。输出1，2.
2. 此时2的左孩子不为NULL，且top==0不满足。所以指针指向2的左孩子，此时栈为1，2，4.输出1，2，4
3. 4的左右孩子为空，所以4退栈，不打印。栈顶指针-1.访问2的右孩子。此时栈为1，2，5.同理，5的左右孩子为空，5退栈，输出1，2，4，5
4. 2的左孩子遍历完毕，所以2退栈，然后同理遍历1的右孩子。
5. 3入栈，然后判断。此时栈为1，3.输出1，2，4，5，3
6. 继续深入，6入栈，此时栈为1，3，6。输出1，2，4，5，3，6.6无左右孩子，6退栈。此时栈为1，3
7. 继续遍历3的右孩子，7入栈。此时栈为1，3，7.7无左右孩子，7退栈。不打印。3左右孩子遍历完，3退栈。1的左右孩子遍历完，1退栈。输出1，2，4，5，3，6，7。退出第一层while循环。非递归函数调用完毕。

       打印输出结果。与递归的简单语句相比，非递归的过程无疑显得更加复杂。但是非递归仍然有其存在的必要性。因为并非所有的程序设计语言都允许递归，而且递归的可读性一般不好，执行效率也不高。所以非递归有时候也是一个很好的选择。

2.概要设计：

               使用C语言，设计了以下函数：

函数	作用
NRPreOrder()	非递归函数，完成非递归函数的主要过程
CreateBiTree()	创建二叉树
PreOrder()	输出二叉树
Main()	主函数，完成函数的调用并打印输出结果

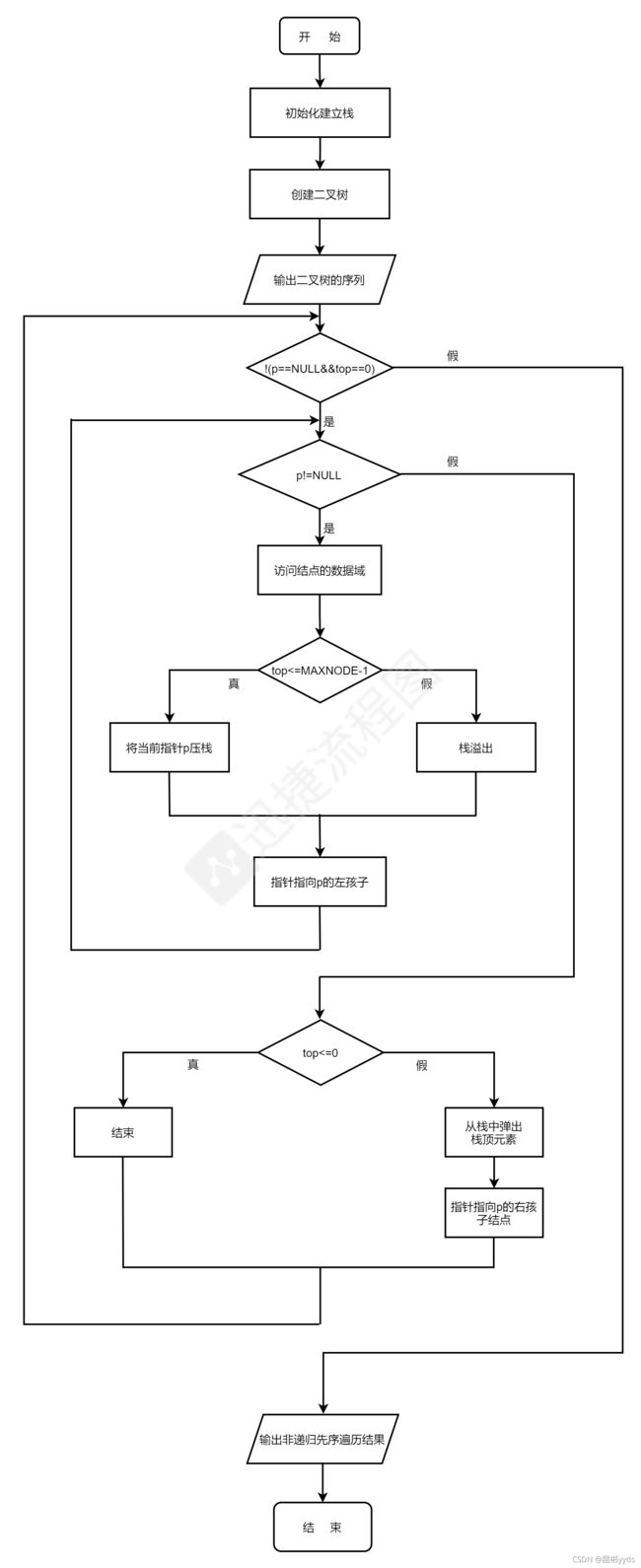
3.程序的运行流程图：

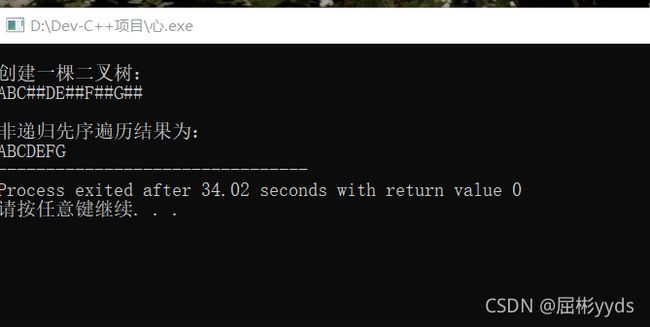
 4.测试

5.总结

       通过这道题，是一个先序遍历的非递归过程，其实主要就是两个while函数的嵌套，另外就是栈在其中的应用。注意进栈的顺序不是输出结果的顺序。不要在理解上走了一些弯路。

6.源代码（Dev-c++ 5.11调试通过）：

#include
#include
#include
#define MAX 200
#define datatype char
typedef char TElemType;
typedef int Status;
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
#define MAXNOODE 200
typedef struct
{
	datatype elem[MAXNOODE];
	int top;
}SeqStack;
SeqStack *p;
//先序创建二叉树
void CreateBiTree(BiTree *T)
{
	char ch;
	ch=getchar();
	if(ch=='#')(*T)=NULL;   //#代表空指针
	   else
	   {
	   	    (*T)=(BiTree)malloc(sizeof(BiTNode));  //申请结点
			CreateBiTree(&(*T)->lchild);           //构造左子树
			(*T)->data=ch;                         //生成根节点
			CreateBiTree(&(*T)->rchild);           //构造右子树 
		} 
 } 
//中序输出二叉树 
//非递归方式遍历二叉树
void visite(BiTNode *node){
 printf("%c",node);
}
void NRPreOrder(BiTree bt)
{//非递归先序遍历二叉树 
	BiTree stack[MAXNOODE],p;
	int top;
	if(bt==NULL)return;
	top=0;
	p=bt;
	while(!(p==NULL&&top==0))
	{  while(p!=NULL)
       {  visite(p->data);     //访问结点的数据域
	      if(top<=MAXNOODE-1)  //将当前指针p入栈
		  {  stack[top]=p; 
		  	 top++;
		  } 
	  else
	  		  {
		  	printf("栈溢出");
		  	return;
		  }
		  p=p->lchild;         //指针指向p的左孩子 
	   }
	   if(top<=0)return;       //栈空时结束 
	   else
	   {
	   	   top--;
	   	   p=stack[top];       //从栈中弹出栈顶元素
		   p=p->rchild;        //指针指向p的右孩子结点 
		} 
	} 
} 
void main()
{
	BiTree T=NULL;
	printf("\n创建一棵二叉树：\n");
	CreateBiTree(&T);
	printf("\n非递归先序遍历结果为：\n");
	NRPreOrder(T); 
}