labuladong算法小抄中图算法的学习笔记(c++版)

首先，建图的时候要注意：通常使用邻接表的形式，而无向图通常建立 双向的邻接表。因此图的数据结构是二维数组!

1 图的遍历

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。
所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
vector<bool> visited;
// 记录从起点到当前节点的路径
vector<int> onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

如果让你处理路径相关的问题，这个 onPath 变量是肯定会被用到的，比如 拓扑排序 中就有运用。

类比贪吃蛇游戏，visited 记录蛇经过过的格子，而 onPath 仅仅记录蛇身。onPath 用于判断是否成环，类比当贪吃蛇自己咬到自己（成环）的场景。

另外，你应该注意到了，这个 onPath 数组的操作很像 回溯算法核心套路 中做「做选择」和「撤销选择」，区别在于位置：回溯算法的「做选择」和「撤销选择」在 for 循环里面，而对 onPath 数组的操作在 for 循环外面。而在 for 循环里面和外面唯一的区别就是对根节点的处理。为什么回溯算法框架会用后者？因为回溯算法关注的不是节点，而是树枝。
对于这里「图」的遍历，我们应该把 onPath 的操作放到 for 循环外面，否则会漏掉记录起始点的遍历。
说了这么多 onPath 数组，再说下 visited 数组，其目的很明显了，由于图可能含有环，visited 数组就是防止递归重复遍历同一个节点进入死循环的。
当然，如果题目告诉你图中不含环，可以把 visited 数组都省掉，基本就是多叉树的遍历。

2 拓扑排序详解及运用

有向图的环检测（无向图的环检测一般用“查并集”）、拓扑排序算法。既可以用 DFS 思路解决，也可以用 BFS 思路解决，相对而言 BFS 解法从代码实现上看更简洁一些，但 DFS 解法有助于你进一步理解递归遍历数据结构的奥义。

环检测算法（DFS 版本）–专为解决依赖环境而生！

【题目】
看到依赖问题，首先想到的就是把问题转化成「有向图」这种数据结构，只要图中存在环，那就说明存在循环依赖。
如果发现这幅有向图中存在环，那就说明课程之间存在循环依赖，肯定没办法全部上完；反之，如果没有环，那么肯定能上完全部课程。常见的存储方式是使用邻接表使问题转换成图结构。
所以我们首先可以写一个建图函数：

vector<int> buildGraph(int numCourses, vector<vector<int>>prerequisites) {
    // 图中共有 numCourses 个节点
    vector<vector<int>>graph(numCourses);
    for (auto edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 添加一条从 from 指向 to 的有向边
        // 边的方向是「被依赖」关系，即修完课程 from 才能修课程 to
        graph[from].push_back(to);
    }
    return graph;
}

前文 图论基础 写了 DFS 算法遍历图的框架，无非就是从多叉树遍历框架扩展出来的，加了个 visited 数组罢了,我们就可以直接套用遍历代码：

// 记录被遍历过的节点
vector<bool> visited;
// 主函数
bool canFinish(int numCourses, vector<vector<int>>prerequisites) {
    vector<vector<int>> graph = buildGraph(numCourses, prerequisites);
    //注意图中并不是所有节点都相连，所以要用一个 for 循环将所有节点都作为起点调用一次 DFS 搜索算法。这样，就能遍历这幅图中的所有节点了
    for (int i = 0; i < numCourses; i++) {
        traverse(graph, i);
    }
}
/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    for (int neighbor : graph[s]) {
        traverse(graph, neighbor);
    }
}

你可以把递归函数看成一个在递归树上游走的指针，这里也是类似的：
你也可以把 traverse 看做在图中节点上游走的指针，只需要再添加一个布尔数组 onPath 记录当前 traverse 经过的路径，这里就有点回溯算法的味道了，在进入节点 s 的时候将 onPath[s] 标记为 true，离开时标记回 false，如果发现 onPath[s] 已经被标记，说明出现了环。
这样，就可以在遍历图的过程中顺便判断是否存在环了，完整代码如下：

// 记录被遍历过的节点，防止走回头路
vector<bool> visited;
// 记录一次递归堆栈中的节点
vector<bool> onPath;
// 记录图中是否有环
bool hasCycle = false;
// 主函数
bool canFinish(int numCourses, vector<vector<int>>prerequisites) {
    vector<vector<int>> graph = buildGraph(numCourses, prerequisites);
    visited.resize(numCourses,false);
    onPath.resize(numCourses,false);

    for (int i = 0; i < numCourses; i++) {
    // 遍历图中的所有节点
        traverse(graph, i);
    }
   // 只要没有循环依赖可以完成所有课程
    return !hasCycle;
}
/* 图遍历框架 */
void traverse(Graph graph, int s) {
	if (onPath[s]) {
        // 出现环
        hasCycle = true;
    }
    if (visited[s] || hasCycle) return;
 // 前序代码位置
    visited[s] = true;
    onPath[s] = true;
    for (int neighbor : graph[s]) {
        traverse(graph, neighbor);
    }
    // 后序代码位置
    onPath[s] = false;
}
vector<int> buildGraph(int numCourses, vector<vector<int>>prerequisites) {
    // 图中共有 numCourses 个节点
    vector<vector<int>>graph(numCourses);
    for (auto edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 添加一条从 from 指向 to 的有向边
        // 边的方向是「被依赖」关系，即修完课程 from 才能修课程 to
        graph[from].push_back(to);
    }
    return graph;
}

不过如果出题人继续恶心你，让你不仅要判断是否存在环，还要返回这个环具体有哪些节点，怎么办？

拓扑排序算法（DFS 版本）

这道题就是上道题的进阶版，不是仅仅让你判断是否可以完成所有课程，而是进一步让你返回一个合理的上课顺序，保证开始修每个课程时，前置的课程都已经修完。什么是拓扑排序呢？

直观地说就是，让你把一幅图「拉平」，而且这个「拉平」的图里面，所有箭头方向都是一致的。
首先，我们先判断一下题目输入的课程依赖是否成环，成环的话是无法进行拓扑排序的，所以我们可以复用上一道题的主函数：

public vector<int> findOrder(int numCourses, vector<vector<int>> prerequisites) {
    if (!canFinish(numCourses, prerequisites)) {
        // 不可能完成所有课程
        return new int[]{};
    }
    // ...
}

其实特别简单，将后序遍历的结果进行反转，就是拓扑排序的结果。

：有的读者提到，他在网上看到的拓扑排序算法不用对后序遍历结果进行反转，这是为什么呢？你确实可以看到这样的解法，原因是他建图的时候对边的定义和我不同。我建的图中箭头方向是「被依赖」关系，比如节点 1 指向 2，含义是节点 1 被节点 2 依赖，即做完 1 才能去做 2，如果你反过来，把有向边定义为「依赖」关系，那么整幅图中边全部反转，就可以不对后序遍历结果反转。具体来说，就是把我的解法代码中 graph[from].add(to); 改成 graph[to].add(from); 就可以不反转了。

在上一题环检测的代码基础上添加了记录后序遍历结果的逻辑：

// 记录被遍历过的节点，防止走回头路
vector<bool> visited， onPath;
// 记录一次递归堆栈中的节点
vector<int> postorder ;
// 记录图中是否有环
bool hasCycle = false;
// 主函数
vector<int> findOrder(int numCourses, vector<vector<int>>prerequisites) {
    vector<vector<int>> graph = buildGraph(numCourses, prerequisites);
    visited.resize(numCourses,false);
    onPath.resize(numCourses,false);

    for (int i = 0; i < numCourses; i++) {
    // 遍历图中的所有节点
        traverse(graph, i);
    }
  // 有环图无法进行拓扑排序
    if (hasCycle) {
        return {};
    }
     // 逆后序遍历结果即为拓扑排序结果
    reverse(postorder.begin(),postorder.end());
    return postorder;
}
/* 图遍历框架 */
void traverse(Graph graph, int s) {
	if (onPath[s]) {
        // 出现环
        hasCycle = true;
    }
    if (visited[s] || hasCycle) return;
 // 前序代码位置
    visited[s] = true;
    onPath[s] = true;
    for (int neighbor : graph[s]) {
        traverse(graph, neighbor);
    }
    // 后序遍历位置
    postorder.push_back(s);
    // 后序代码位置
    onPath[s] = false;
}
vector<vector<int>> buildGraph(int numCourses, vector<vector<int>>prerequisites) {
    // 图中共有 numCourses 个节点
    vector<vector<int>>graph(numCourses);
    for (auto edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 添加一条从 from 指向 to 的有向边
        // 边的方向是「被依赖」关系，即修完课程 from 才能修课程 to
        graph[from].push_back(to);
    }
    return graph;
}

那么为什么后序遍历的反转结果就是拓扑排序呢？
后序遍历的这一特点很重要，之所以拓扑排序的基础是后序遍历，是因为一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行。这个有数学证明，不过这里记住就可以了！

环检测算法（BFS 版本）

其实 BFS 算法借助 indegree 数组记录每个节点的「入度」，也可以实现这两个算法。
我先总结下这段 BFS 算法的思路：
1、构建邻接表，和之前一样，边的方向表示「被依赖」关系。
2、构建一个 indegree 数组记录每个节点的入度，即 indegree[i] 记录节点 i 的入度。
3、对 BFS 队列进行初始化，将入度为 0 的节点首先装入队列。
4、开始执行 BFS 循环，不断弹出队列中的节点，减少相邻节点的入度，并将入度变为 0 的节点加入队列。
5、如果最终所有节点都被遍历过（count 等于节点数），则说明不存在环，反之则说明存在环。
只要是最终队列处理完毕后，入度仍不为0的点，就是构成环的点（详解可见拓展题）
代码如下：

// 主函数
bool canFinish(int numCourses, vector<vector<int>>prerequisites) {
    // 建图，有向边代表「被依赖」关系
    vector<vector<int>>graph = buildGraph(numCourses, prerequisites);
    // 构建入度数组
    vector<int>indegree（numCourses）;
    for (vector<int> edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 节点 to 的入度加一
        indegree[to]++;
    }

    // 根据入度初始化队列中的节点
    deque<int> q;
    for (int i = 0; i < numCourses; i++) {
        if (indegree[i] == 0) {
            // 节点 i 没有入度，即没有依赖的节点
            // 可以作为拓扑排序的起点，加入队列
            q.push_back(i);
        }
    }

    // 记录遍历的节点个数
    int count = 0;
    // 开始执行 BFS 循环
    while (!q.empty()) {
        // 弹出节点 cur，并将它指向的节点的入度减一
        int cur = q.front();
        q.pop_front();
        count++;
        for (int next : graph[cur]) {
            indegree[next]--;
            if (indegree[next] == 0) {
                // 如果入度变为 0，说明 next 依赖的节点都已被遍历
                q.push_back(next);
            }
        }
    }
    // 如果所有节点都被遍历过，说明不成环
    return count == numCourses;
}
// 建图函数
vecror<vector<int>> buildGraph(int n, vector<vector<int>> edges) {
    // 见前文
}

为何说存在节点没被遍历就是有环呢：

拓扑排序算法（BFS 版本）

如果你能看懂 BFS 版本的环检测算法，那么就很容易得到 BFS 版本的拓扑排序算法，因为节点的遍历顺序就是拓扑排序的结果。
比如刚才举的第一个例子，下图每个节点中的值即入队的顺序：

显然，这个顺序就是一个可行的拓扑排序结果。
所以，我们稍微修改一下 BFS 版本的环检测算法，记录节点的遍历顺序即可得到拓扑排序的结果：

// 主函数
bool canFinish(int numCourses, vector<vector<int>>prerequisites) {
    // 建图，有向边代表「被依赖」关系
    vector<vector<int>>graph = buildGraph(numCourses, prerequisites);
    // 构建入度数组
    vector<int>indegree（numCourses）;
    for (vector<int> edge : prerequisites) {
        int from = edge[1], to = edge[0];
        // 节点 to 的入度加一
        indegree[to]++;
    }

    // 根据入度初始化队列中的节点
    deque<int> q;
    for (int i = 0; i < numCourses; i++) {
        if (indegree[i] == 0) {
            // 节点 i 没有入度，即没有依赖的节点
            // 可以作为拓扑排序的起点，加入队列
            q.push_back(i);
        }
    }
    // 记录遍历的节点个数
    int count = 0;
    // 记录拓扑排序结果
    vector<int> res(numCourses);
    // 开始执行 BFS 循环
    while (!q.empty()) {
        // 弹出节点 cur，并将它指向的节点的入度减一
        int cur = q.front();
        q,pop_front();
        res.push_back(cur);
        count++;
        for (int next : graph[cur]) {
            indegree[next]--;
            if (indegree[next] == 0) {
                // 如果入度变为 0，说明 next 依赖的节点都已被遍历
                q.push_back(next);
            }
        }
    }
    if (count != numCourses) 
    {
        // 存在环，拓扑排序不存在
        return {};
    }
    return res;
}
// 建图函数
 vector<vector<int>>buildGraph(int n, int[][] edges) {
    // 见前文
}

小应用 444.重建序列（子序列&唯一的拓扑排序）

这个其实所谓超序列也是一个依赖关系出来的序列。其是1，n的整数排列，也代表着有n个节点。
因为sequence是子序列组，其关键信息就是他们之间是有前后顺序的（也就是有依赖）。因此超序列其实是这些有依赖的组拓扑排序的结果。因此我们可以先根据sequence来建立有向图，随后拓扑排序进行数据比较即可。
但有两个细节需要注意：一是由于其sequence已经规定是nums的子序列，因此无需担心环问题；二是因为其超序列还有一个唯一的要求，而我们知道，拓扑排序是有可能有多个顺序的，因此我们为了满足唯一，就需要给队列进行处理，如果有多个在等待出队时，那么不唯一，直接返回false。

class Solution {
public:
    bool sequenceReconstruction(vector<int>& nums, vector<vector<int>>& sequences) {
        int n = nums.size();
        vector<unordered_set<int>>graph(n+1);//因为边在有可能重复出现，因此这里用哈希表防止重复
        vector<int>indegree(n+1);
        vector<int>ans;
        //完成图以及入度数组的初始化
        for(auto &sequence : sequences)
        {
            for(int i=1;i<sequence.size();i++)//毕竟sequence长度不一定为2
            {
                if(graph[sequence[i-1]].count(sequence[i])) continue;
                graph[sequence[i-1]].insert(sequence[i]);
                indegree[sequence[i]]++;
            }
        }
        deque<int>dq;
        //加载开头
        for(int i=1;i<n+1;i++)
        {
            if(indegree[i]==0) dq.push_back(i);
        }
        //开始排序
        while(!dq.empty())
        {
            //保证唯一，必不可少
            if(dq.size()>1) return false;
            int cur = dq.front();
            dq.pop_front();
            ans.push_back(cur);
            for(auto &next:graph[cur])
            {
                indegree[next]--;
                if(indegree[next]==0) dq.push_back(next);
            }
        }
        //最后对比
        return ans==nums;
    }
};

【拓展】分离出环，并计算有向环的长度

第一步,拓扑排序，分离出环：
根据构建出的有向图，依次删除入度为 0 的节点，得到图中所有的环。因此，只要是最终队列处理完毕后，入度仍不为0的点，就是构成环的点，这个概念要熟悉！

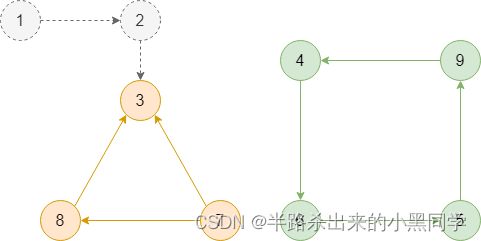
第二步,求出每个环的大小：
可采用深度优先（DFS）或广度优先（BFS）遍历，求出每个环的大小。

class Solution {
public:
    int longestCycle(vector<int>& edges) {
        int n = edges.size();
        vector<int> indegree(n,0);
        vector<bool>in_cycle(n,true);
        //构建入度数组
        for(auto &x:edges) if(x != -1) indegree[x]++;
        //开始拓扑排序找需要删除的非圈节点
        deque<int> dq;
        for(int i=0; i<n; i++)
        {
            if(indegree[i]==0) 
            {
                dq.push_back(i);
                in_cycle[i] = false;//对应删除一步,当然不用真删除
            }
        }
        while(!dq.empty())
        {
            int root = dq.front();
            dq.pop_front();
            if(edges[root]!=-1 && --indegree[edges[root]] == 0)
            {
                dq.push_back(edges[root]);
                in_cycle[edges[root]] = false;
            }
        }
        //遍历所有点，对属于圈里面的点进行个数的统计
        int ans = -1;
        for(int i=0; i<n; i++)
        {
            if(in_cycle[i]) ans = max(ans, bfs(edges, in_cycle, i));
        }
        return ans;

    }
    int bfs(vector<int>& edges, vector<bool>& in_cycle, int x)
    {
        unordered_set<int>visit;
        deque<int>dq2;
        int ans = 0;
        dq2.push_back(x);
        visit.insert(x);
        while(!dq2.empty())
        {
            int root = dq2.front();
            dq2.pop_front();
            ans++;
            in_cycle[root] = false;
            if(edges[root]!=-1 && !visit.count(edges[root]))
            {
                dq2.push_back(edges[root]);
                visit.insert(edges[root]);
            }
        }
        return ans;
    }
};

3 二分图判定

【定义】二分图的顶点集可分割为两个互不相交的子集，图中每条边依附的两个顶点都分属于这两个子集，且两个子集内的顶点不相邻。

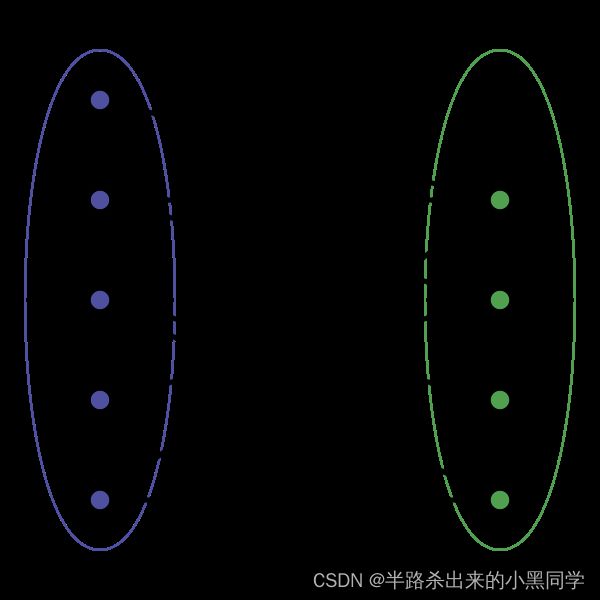
【通俗理解】给你一幅「图」，请你用两种颜色将图中的所有顶点着色，且使得任意一条边的两个端点的颜色都不相同，你能做到吗？如果你能够成功地将图染色，那么这幅图就是一幅二分图，反之则不是：

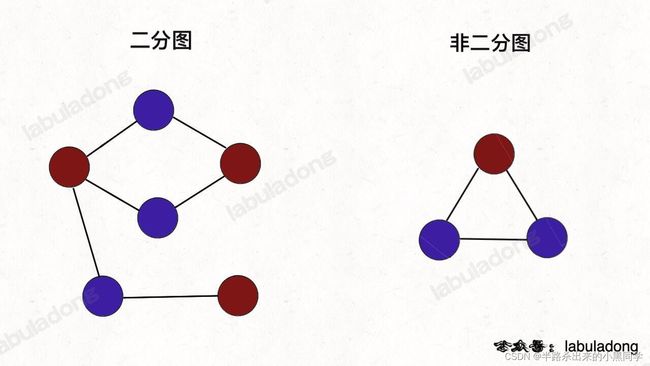
从简单实用的角度来看，二分图结构在某些场景可以更高效地存储数据。
【例子】某一部电影肯定是由多位演员出演的，且某一位演员可能会出演多部电影。你使用什么数据结构来存储这种关系呢？
显然，如果用哈希表存储，需要两个哈希表分别存储「每个演员到电影列表」的映射和「每部电影到演员列表」的映射。但如果用「图」结构存储，将电影和参演的演员连接，很自然地就成为了一幅二分图：

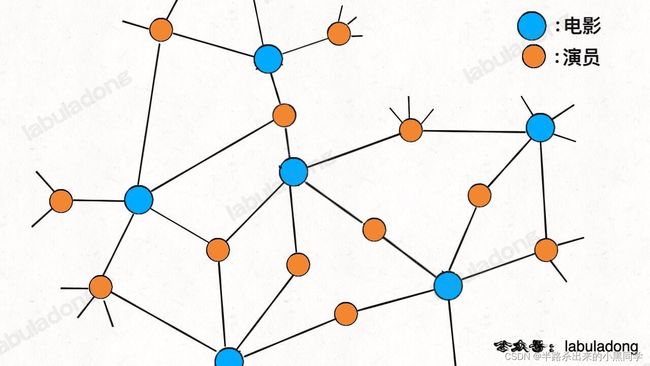
二分图的判定（DFS版本框架）

说白了就是遍历一遍图，一边遍历一边染色，看看能不能用两种颜色给所有节点染色，且相邻节点的颜色都不相同。
而在之前的遍历中，我们都是通过visited数组来防止我们兜圈子遍历，而这次染色中，为了使得相邻的染色不同，务必就要用到visited以来知道哪些节点染了色，哪些节点没染色。

/* 图遍历框架 */
void traverse(Graph graph, vector<bool> visited, int v) {
    visited[v] = true;
    // 遍历节点 v 的所有相邻节点 neighbor
    for (int neighbor : graph.neighbors(v)) {
        if (!visited[neighbor]) {
            // 相邻节点 neighbor 没有被访问过
            // 那么应该给节点 neighbor 涂上和节点 v 不同的颜色
            traverse(graph, visited, neighbor);
        } else {
            // 相邻节点 neighbor 已经被访问过
            // 那么应该比较节点 neighbor 和节点 v 的颜色
            // 若相同，则此图不是二分图
        }
    }
}

以力扣785为例

class Solution {
public:
	// 记录图是否符合二分图性质
    bool flag = true;
    // 记录图中节点的颜色，false 和 true 代表两种不同颜色
    vector<bool>visited;
    // 记录图中节点是否被访问过
    vector<bool>color;
    // 主函数，输入邻接表，判断是否是二分图
    bool isBipartite(vector<vector<int>>& graph) {
        int n =graph.size();
        visited.resize(n,false);
        color.resize(n,false);
    // 因为图不一定是联通的，可能存在多个子图
    // 所以要把每个节点都作为起点进行一次遍历
    // 如果发现任何一个子图不是二分图，整幅图都不算二分图
        for(int i=0;i < n;++i)
        {
            traverse(graph,i);
            if(flag==false) return false;
        }
        return true;
    }
    void traverse(vector<vector<int>>& graph,int i)
    {
        visited[i] = true;
        for(auto j : graph[i])
        {
            if(!visited[j])
            {
                color[j] = !color[i];
                traverse(graph,j);
            }
            else
            {
                if(color[i]==color[j]) flag=false;
            }
        }
    }
};

二分图的判定（BFS版本框架）

class Solution {
public:
	// 记录图是否符合二分图性质
    bool flag = true;
    // 记录图中节点的颜色，false 和 true 代表两种不同颜色
    vector<bool>visited;
    // 记录图中节点是否被访问过
    vector<bool>color;
    // 主函数，输入邻接表，判断是否是二分图
    bool isBipartite(vector<vector<int>>& graph) {
        int n =graph.size();
        visited.resize(n,false);
        color.resize(n,false);
    // 因为图不一定是联通的，可能存在多个子图
    // 所以要把每个节点都作为起点进行一次遍历
    // 如果发现任何一个子图不是二分图，整幅图都不算二分图
        for(int i=0;i < n;++i)
        {
            BFS(graph,i);
            if(flag==false) return false;
        }
        return true;
    }
    void BFS(vector<vector<int>>& graph,int i)
    {
      deque<int> dq;
        visited[i] = true;
        dq.push_back(i);
        while(!dq.empty())
        {
        // 从节点 v 向所有相邻节点扩散
            int j = dq.front();
            dq.pop_front();
            for(auto h:graph[j])
            {
                if(!visited[h])
                // 相邻节点 h 没有被访问过
                // 那么应该给节点 h 涂上和节点 j 不同的颜色
                {
                    color[h] = !color[j];
                    // 标记 h 节点，并放入队列
                    visited[h] = true;
                    dq.push_back(h);
                }
                else 
                {
                // 相邻节点 h 已经被访问过
                // 根据 j 和 h 的颜色判断是否是二分图
                // 若相同，则此图不是二分图
                    if(color[h]==color[j])
                    {
                        flag = false;
                        return;
                    }
                }
            }
        }
    }
};

4 关于BFS的一个小总结

indegree 数组只适用于拓扑排序的场景（环检测其实就是拓扑排序的一种情况，毕竟有环就没法拓扑排序了），其他场景的 BFS/DFS 遍历都是配合 visited 数组进行的。

5 DIJKSTRA 算法模板—要求不能存在负权重边

音译：迪杰斯特拉算法，无非就是一个 BFS 算法的加强版，它们都是从二叉树的层序遍历衍生出来的

BFS框架----无权值最短路径算法

所谓 BFS 算法，就是把算法问题抽象成一幅「无权图」，然后继续玩二叉树层级遍历那一套罢了。
适用于无权有向图，可以有环，一般是求两点的最短路径，也可以改进为求起点到其它所有点的最短路径

// 输入起点，进行 BFS 搜索
int BFS(Node* start) {
    deque<Node*> q; // 核心数据结构
    unordered_set<Node*> visited; // 避免走回头路
     
    q.push_back(start); // 将起点加入队列
    visited.insert(start);

    int step = 0; // 记录搜索的步数
    while (!q.empty()) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散一步 */
        for (int i = 0; i < sz; i++) {
            Node* cur = q.front();
            q.pop_front();
            printf("从 %s 到 %s 的最短距离是 %s", start, cur, step);
            /* 将 cur 的相邻节点加入队列 */
            for (auto x : cur.adj()) {
                if (x not in visited) {
                    q.push_back(x);
                    visited.insert(x);
                }
            }
        }
        step++;
    }
}

注意，我们的 BFS 算法框架也是 while 循环嵌套 for 循环的形式，也用了一个 step 变量记录 for 循环执行的次数，无非就是多用了一个 visited 集合记录走过的节点，防止走回头路罢了。
而对于有权图，我们并不能再轻易使用BFS了，而是需要使用DIJKSTRA 算法，其与BFS相比，有以下区别：
1、去掉了 while 循环里面的 for 循环，因为这个for在树结构有区别层的含义，在无权图中有区别步数的含义，而对于有权图来说向外扩散是要求路径和的，因此不需要for。
2、还需要一个state类来辅助一下

struct State {
    // 图节点的 id
    int id;
    // 从 start 节点到当前节点的距离
    int distFromStart;
    //此处重构小于号，是因为下面用到最小堆的优先队列
    bool operator < (const State& rhs) const
    {
    	return distFromStart > rhs.distFromstart;
    }
    State(int x,int y):id(x),disFromStart(y){};
}

类似刚才二叉树的层序遍历，我们也需要用 State 类记录一些额外信息，也就是使用 distFromStart 变量记录从起点 start 到当前这个节点的距离。

dijkstra框架----加权有向图的最短路径

【目的】输入是一幅图 graph 和一个起点 start，返回是一个记录最短路径权重的数组。适用于加权有向图，没有负权重边，且无环，一般是求起点到其它所有点的最短路径，也可以改进为求两点的最短路径。
【要点】加权图中的 Dijkstra 算法和无权图中的普通 BFS 算法不同，在 Dijkstra 算法中，你第一次经过某个节点时的路径权重，不见得就是最小的，所以对于同一个节点，我们可能会经过多次，而且每次的 distFromStart 可能都不一样，比如下图：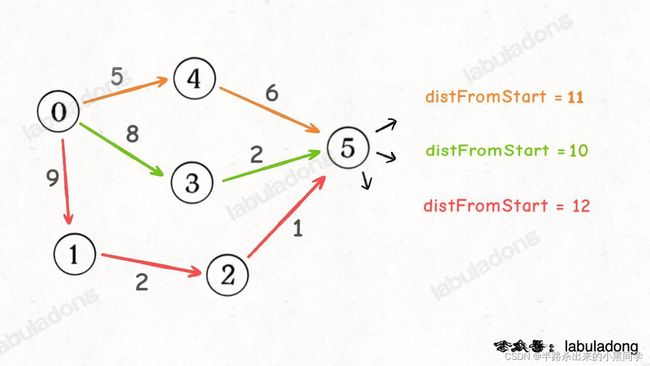
因此，我们不能再使用visited了。其实，Dijkstra 可以理解成一个带 dp table（或者说备忘录）的 BFS 算法，伪码如下：

// 返回节点 from 到节点 to 之间的边的权重
int weight(int from, int to);

// 输入节点 s 返回 s 的相邻节点
vector<int> adj(int s);

// 输入一幅图和一个起点 start，计算 start 到其他节点的最短距离
vector<int> dijkstra(int start, vector<int> graph) {
    // 图中节点的个数
    int V = graph.size();
    // 记录最短路径的权重，你可以理解为 dp table
    // 定义：distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
    // 求最小值，所以 dp table 初始化为正无穷
    vector<int>distTo(V,INT_MAX);
    // base case，start 到 start 的最短距离就是 0
    distTo[start] = 0;

    // 优先级队列，distFromStart 较小的排在前面
    priority_queue<State> pq;
    // 从起点 start 开始进行 BFS
    pq.push(State(start, 0));

    while (!pq.empty()) {
        State curState = pq.top();
        pq.pop();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;

        if (curDistFromStart > distTo[curNodeID]) {
            // 已经有一条更短的路径到达 curNode 节点了
            //这一句与下面的优先队列配合来提高效率
            continue;
        }
        // 将 curNode 的相邻节点装入队列
        for (int nextNodeID : adj(curNodeID)) {
            // 看看从 curNode 达到 nextNode 的距离是否会更短
            int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
            if (distTo[nextNodeID] > distToNextNode) {
                // 更新 dp table
                distTo[nextNodeID] = distToNextNode;
                // 将这个节点以及距离放入队列
                pq.push(State(nextNodeID, distToNextNode));
            }
        }
    }
    return distTo;
}

本框架相比BFS的三个特点：
1、无需visited，因为入队是有条件的，因此不会陷入无限循环
2、这里使用了优先队列，其实普通队列也对，也可以，但是使用优先队列会优先探索已知路径和少的节点，类似于贪心，因此效率会高一些。
3、如果查找一个特定的点到点距离，只需要加一个if即可,因为优先队列的效果，甚至都不用专门去判断。

// 输入起点 start 和终点 end，计算起点到终点的最短距离
int dijkstra(int start, int end, vector<int> graph) {
    // ...
    while (!pq.empty()) {
        State curState = pq.top();
        pq.pop();
        int curNodeID = curState.id;
        int curDistFromStart = curState.distFromStart;
        // 在这里加一个判断就行了，其他代码不用改
        // 加在上面下面都OK
        if (curNodeID == end) {
            return curDistFromStart;
        }
        if (curDistFromStart > distTo[curNodeID]) {
            continue;
        }
        // ...
    }
    // 如果运行到这里，说明从 start 无法走到 end
    return INT_MAX;
}

步骤总结及例题应用

和BFS大体流程真的很像
【步骤】
0、完成自定义类（其有id和distance（这就是该点到起点的距离）两个属性），并重写<符号（为优先队列做好准备）
1、建立距离数组（其需要存放从起点到各点的距离），并完成初始化（起点赋0，其他INT_MAX）。
2、建立优先队列，并完成初始化。（把起点实例创建的类，再放进去，其实就是BFS过程）
3、像BFS一样，while循环队列，取出在堆顶的节点。
4、【该点的判断】判断一下，取出来的点与起点的距离与距离数组中记录的距离谁更小一些，如果新取出来的比较大就不走这条路了。（配合优先队列完成程序优化，因为优先队列先走路短的，而路长却加进队列的，一判断立马continue就ok）
5、【处理邻点】for循环该点的邻点，如果该点的距离加上到邻点的权重能比距离数组记录中的起点到邻点的距离更小，就更新距离数组并将邻点加入新的优先队列，从这个点再准备走下去。

class Solution {
public:
	//题解函数
    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<vector<pair<int, int>>> graph = build_graph(times, n);
        vector<int> dis = dijkstra(graph,k);
        int ans = 0;
        for(int i=1;i<dis.size();++i)
        {
            ans = max(ans,dis[i]);
        }
        if(ans == INT_MAX) return -1;
        return ans;
    }
    //建图函数
    vector<vector<pair<int, int>>>build_graph(vector<vector<int>>& times, int n)
    {
        vector<vector<pair<int, int>>>graph(n+1);
        for(auto time:times)
        {
            graph[time[0]].push_back({time[1],time[2]});
        }
        return graph;
    }
    //dijkstra算法
       // 输入一幅图和一个起点 start，计算 start 到其他节点的最短距离
    vector<int> dijkstra(vector<vector<pair<int, int>>>graph,int start)
    {
        // 图中节点的个数
        int n = graph.size();
        // 记录最短路径的权重，你可以理解为 dp table
        // 定义：distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
        // 求最小值，所以 dp table 初始化为正无穷
        vector<int>dis_to(n,INT_MAX);
        // base case，start 到 start 的最短距离就是 0
        dis_to[start] = 0;
        // 优先级队列，distFromStart 较小的排在前面
        priority_queue<State> pq;
        // 从起点 start 开始进行 BFS
        pq.push(State(start,0));
        while(!pq.empty())
        {
            State cur_state = pq.top();
            pq.pop();
            // 已经有一条更短的路径到达 curNode 节点了
            //这一句与下面的优先队列配合来提高效率
            if(cur_state.distance > dis_to[cur_state.id]) continue;
            // 将 curNode 的相邻节点装入队列
            for(auto point:graph[cur_state.id])
            {
                int next_dis = dis_to[cur_state.id] + point.second;
                // 看看从 curNode 达到 nextNode 的距离是否会更短
                if(dis_to[point.first] > next_dis)
                {
                    // 更新 dp table
                    dis_to[point.first] = next_dis;
                    // 将这个节点以及距离放入队列
                    pq.push(State(point.first,next_dis));
                }
            }
        }
        return dis_to;
    }
private:
	//设立的类结构，方便配合优先队列
    struct State
    {
        int id;
        int distance;
        bool operator <  (const State& rhs)const{
            return distance > rhs.distance;
        }
        State(int x,int y):id(x),distance(y){};
    };
};

dijkstra的对立面框架----最长路径？无向图？

看完这个题肯定会与框架有两个冲突：
1、无向图？其实无向图本质上可以认为是「双向图」，从而转化成有向图。因此在建图的时候直接双向就可以搞定了！
2、最大值？Dijkstra 计算最短路径的正确性依赖一个前提：路径中每增加一条边，路径的总权重就会增加。那么对于最大值：路径中每增加一条边，路径的总权重就会减少，要是能够满足这个条件，也可以用 Dijkstra 算法。而题目是满足的，因此也可以使用dijkstra算法。实际使用方法只需要修改优先队列的排列顺序和一些if的大小判断。
3、有end，那么就加个判断，如果队列取出来的编号为end，那么返回距离数组中的end记录即可。

class Solution {
public:
    double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
        vector<vector<pair<int,double>>> graph = build_graph(n,edges,succProb);
        double ans = dijkstra(graph,start,end);
        return ans;
    }
    vector<vector<pair<int,double>>> build_graph(int n, vector<vector<int>>& edges, vector<double>& succProb)
    {
        vector<vector<pair<int,double>>>graph;
        graph.resize(n);
        //由于无向图就是双向图，因此建图这边就可以搞定这个问题
        for(int i=0;i<edges.size();++i)
        {
            graph[edges[i][0]].push_back({edges[i][1],succProb[i]});
            graph[edges[i][1]].push_back({edges[i][0],succProb[i]});
        }
        return graph;
    }
    double dijkstra(vector<vector<pair<int,double>>>graph,int start, int end)
    {
        int n = graph.size();
        vector<double>disto(n,0);
        disto[start] = 1;
        priority_queue<State>pq;
        pq.push(State(start,1));
        while(!pq.empty())
        {
            State cur_point = pq.top();
            pq.pop();
            //这里加判断即可，与下面的判断无所谓谁先谁后，
            //不过放在前面可以快点，就算cur_point.distance都可以
            //可以好好想想，其实就是因为好几个选择。
            //但由于优先队列，最前面的是肯定就是最长的那个路。
            if(cur_point.id == end) return disto[cur_point.id];
            //勿忘修改if
            if(cur_point.distance < disto[cur_point.id]) continue;
            for(auto neighbor : graph[cur_point.id])
            {
                double next_dis = neighbor.second * disto[cur_point.id];
                //勿忘修改if
                if(next_dis > disto[neighbor.first])
                {
                    disto[neighbor.first] = next_dis;
                    pq.push(State(neighbor.first,next_dis));
                }
            }
        }
        return 0;
    }
private:
    struct State{
        int id;
        double distance;
        State(int x, double y):id(x),distance(y){};
        //注意优先队列的运算符是需要修改好的
        bool operator < (const State &rhs)const{
            return distance < rhs.distance;
        }
    };
};

6 并查集(UNION-FIND)算法详解

其实，这个算法主要是解决图论中「动态连通性」问题的。首先解释一下什么是动态连通性：
简单说，动态连通性其实可以抽象成给一幅图连线。比如下面这幅图，总共有 10 个节点，他们互不相连，分别用 0~9 标记：

而算法主要实现三个功能：

class UF {
    /* 将 p 和 q 连接 */
    void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    bool connected(int p, int q);
    /* 返回图中有多少个连通分量 */
    int count();
}

以上图为例，0～9 任意两个不同的点都不连通，调用 connected 都会返回 false，连通分量为 10 个。
如果现在调用 union(0, 1)，那么 0 和 1 被连通，连通分量降为 9 个。
再调用 union(1, 2)，这时 0,1,2 都被连通，调用 connected(0, 2) 也会返回 true，连通分量变为 8 个。
判断这种「等价关系」非常实用，比如说编译器判断同一个变量的不同引用，比如社交网络中的朋友圈计算等等。

基本框架

数据结构

我们可以使用森林（若干棵树）来表示图的动态连通性，用数组来具体实现这个森林(主要是需要父节点)。

class UF {
    // 记录连通分量
    int count;
    // 节点 x 的父节点是 parent[x]
    vector<int> parent;

    /* 构造函数，n 为图的节点总数 */
    public UF(int n) {
        // 一开始都互不连通
        count = n;
        // 父节点指针初始指向自己
        for (int i = 0; i < n; i++)
            parent[i] = i;
    }
    /* 其他函数 */
}

连接

如果某两个节点被连通，则让其中的（任意）一个节点的根节点接到另一个节点的根节点上：

void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 将两棵树合并为一棵
    parent[rootP] = rootQ;
    // parent[rootQ] = rootP 也一样
    count--; // 两个分量合二为一，因此联通量少一个
}

/* 返回某个节点 x 的根节点 */
int find(int x) {
    // 根节点的 parent[x] == x
    while (parent[x] != x)
        x = parent[x];
    return x;
}
/* 返回当前的连通分量个数 */
int count() { 
    return count;
}

查询是否连通

如果节点 p 和 q 连通的话，它们一定拥有相同的根节点：

bool connected(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    return rootP == rootQ;
}

复杂度分析

find , union , connected 的时间复杂度都是 O(N)。这个复杂度很不理想的，你想图论解决的都是诸如社交网络这样数据规模巨大的问题，对于 union 和 connected 的调用非常频繁，每次调用需要线性时间完全不可忍受。原因其实在于其一般会变得极端不平衡，因此应尽量优化树形，使其逼近平衡二叉树的logN复杂度，甚至更低。

优化后框架

一共有两个角度，两种方法！
1、重量–优化大约至logN。（淘汰，可以学一下思想）
主要是修改连接函数
简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面，那么这里就可能出现「头重脚轻」的不平衡状况，比如下面这种局面：

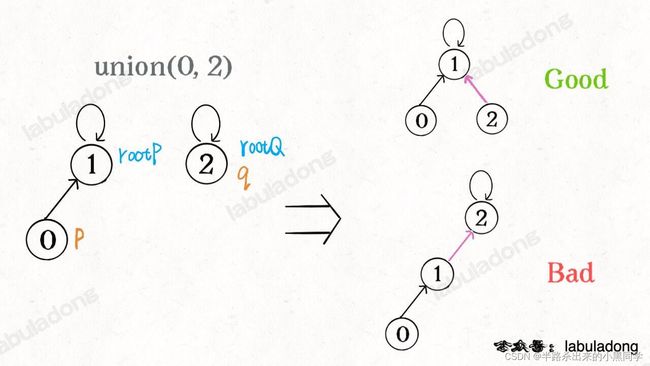
因此我们需要让小一些的树接到大一些的树上面，因此我们额外使用一个size数组。

class UF {
    int count;
    vector<int> parent;
    // 新增一个数组记录树的“重量”
    vector<int> size;
    public UF(int n) {
        count = n;
        // 最初每棵树只有一个节点
        // 重量应该初始化 1
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 小树接到大树下面，较平衡
    if (size[rootP] > size[rootQ]) {
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ];
    } else {
        parent[rootP] = rootQ;
        size[rootQ] += size[rootP];
    }
    count--;
}
}

2、路径压缩（压缩至O(1)，常用）
其实我们并不在乎每棵树的结构长什么样，只在乎根节点。要做到这一点主要是修改 find 函数逻辑，其实有迭代方法的，就是加个
parent[x] = parent[parent[x]];但此处，还是记住递归的方法把，这个压缩的效率更高，找到根节点，一次性把子节点全更新了!

int find(int x) {
    if (parent[x] != x)  parent[x] = find(parent[x]);
    return parent[x];
}

查并集的框架及其步骤总结

【步骤】
1、主要需要两个成员变量：一个用于统计分量个数、另一个数组来记录父节点。
2、初始化父节点数组，使里面的每个节点都指向自己，表示是一个根节点。
3、（寻找函数）其实就是一个递归，返回需要查找点的父节点。
4、（连接函数）两个find找到两个节点的父节点，若相等就没必要连接了，若不等就直接一个的父节点等于另一个即可，随后统计分量的个数别忘记减一。
5、（查询函数）直接找到父节点，看是否相等就行。

class UF {
    // 连通分量个数
   int count;
    // 存储每个节点的父节点
    vector<int> parent;
    // n 为图中节点的个数
    void UF(int n) 
    {
        count = n;
        parent.resize(n);
        for (int i = 0; i < n; i++) parent[i] = i;
    }
    
    // 将节点 p 和节点 q 连通
    void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;//这步必须有！千万别忘
        
        parent[rootQ] = rootP;
        // 两个连通分量合并成一个连通分量
        count--;
    }

    // 判断节点 p 和节点 q 是否连通
   bool connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }
	int find(int x) {
	//路径压缩yyds
        if (parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }

    // 返回图中的连通分量个数
    public int count() {
        return count;
    }
}

构造函数初始化数据结构需要 O(N) 的时间和空间复杂度；连通两个节点 union、判断两个节点的连通性 connected、计算连通分量 count 所需的时间复杂度均为 O(1)。

例题应用

核心思想是：将 equations 中的算式根据 == 和 != 分成两部分，先处理== 算式，使得他们通过相等关系各自连接起来（连通分量）；然后处理 != 算式，检查不等关系是否破坏了相等关系的连通性。

class Solution {
public:
    int count;
    vector<int>parent;
    bool equationsPossible(vector<string>& equations) {
        //根据变量个数，初始化节点数,初始化算法所需成员变量
        unordered_set<char> record;
        for(auto equation:equations) {record.insert(equation[0]);record.insert(equation[3]);}
        int n = record.size();
        count = n;//这个其实本题没用到
        //注意，此处因为全为英文字母，因此多放几个节点也没啥问题！只要count把持住就行
        parent.resize(26);
        for(int i=0;i<26;i++) parent[i] = i;
        //先构造根据等号连通
        for(auto equation:equations)
        {
            if(equation[1]=='=')
            {
                int x = equation[0] - 'a',y = equation[3] - 'a';
                link(x,y);
            }
        }
        //再根据不等号判断是否冲突
        for(auto equation:equations)
        {
            if(equation[1]=='!')
            {
                int x = equation[0] - 'a',y = equation[3] - 'a';
                if(connected(x,y)) return false;
            }
        }
        return true;
    }
    //查找
    int find(int x)
    {
        if(x!=parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }
    //连接
    void link (int x,int y)
    {
        int x_p = find(x);
        int y_p = find(y);
        if(x_p == y_p) return;
        parent[x_p] = y_p;
        count--;
    }
    //查询
    bool connected(int x,int y)
    {
        int x_p = find(x);
        int y_p = find(y);
        return x_p==y_p;
    }
};

无向图检测环

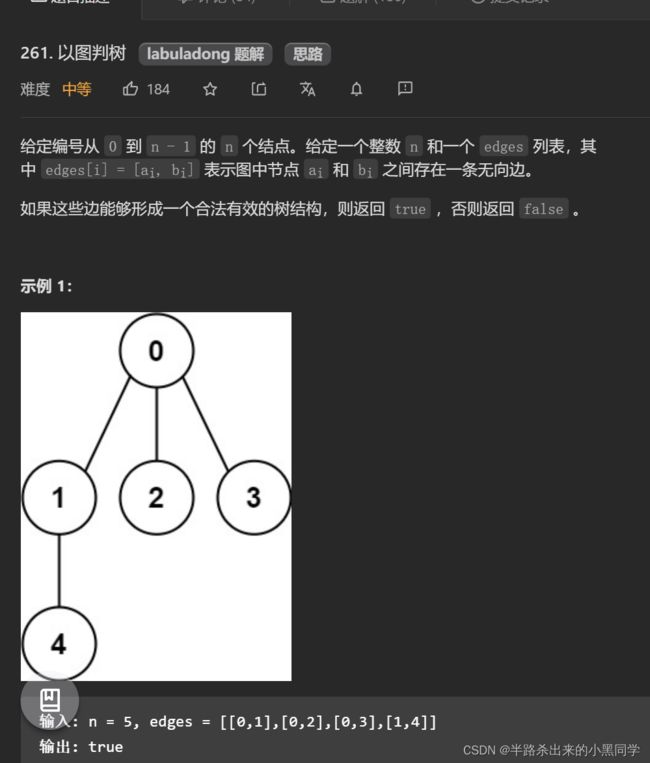
那么这个如何与查并集牵涉上联系呢？
对于添加的这条边，如果该边的两个节点本来就在同一连通分量里，那么添加这条边会产生环；反之，如果该边的两个节点不在同一连通分量里，则添加这条边不会产生环。

class Solution {
public:
vector<int>parent;
int count;//既然形成一个树，那么最后一个应该只剩下一个！
    bool validTree(int n, vector<vector<int>>& edges) {
        count = n;
        parent.resize(n);
        for(int i=0;i<n;++i) parent[i] = i;
        for(auto edge:edges)
        {
            if(!link(edge[0],edge[1])) return false;
        }
        if(count!=1) return false;
        return true;

    }
    int find(int x)
    {
        if(x!=parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }
    bool link(int x,int y)
    {
        int p_x = find(x);
        int p_y = find(y);
        if(p_x == p_y) return false;
        parent[p_x] = p_y;
        count--;
        return true;
    }
};

7 最小生成树算法

最小生成树算法主要有 Prim 算法（普里姆算法）和 Kruskal 算法（克鲁斯卡尔算法）两种，这两种算法虽然都运用了贪心思想，但从实现上来说差异还是蛮大的。

Kruskal算法，该算法以边为单元，时间主要取决于边数，比较适合于稀疏图
Prim算法，该算法以顶点为单元，与图中边数无关，比较适合于稠密图

什么是最小生成树–专为解决无向图连接成本

先说「树」和「图」的根本区别：树不会包含环，图可以包含环。
那么什么是图的「生成树」呢，其实按字面意思也好理解，就是在图中找一棵包含图中的所有节点的树。专业点说，生成树是含有图中所有顶点的「无环连通子图」。而一个图可以划分成多个生成树，如下图：

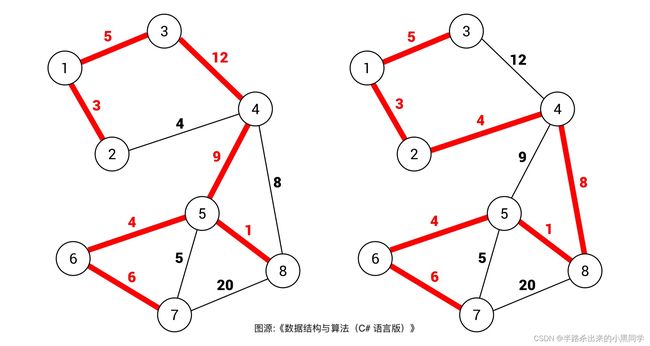
因为对于加权图，每个边都有相应的权重。那么最小生成树很好理解了，所有可能的生成树中，权重和最小的那棵生成树就叫「最小生成树」。

PS：一般来说，我们都是在无向加权图中计算最小生成树的，所以使用最小生成树算法的现实场景中，图的边权重一般代表成本、距离这样的标量。

Kruskal 最小生成树算法–排序+查并集

Kruskal 算法其实很容易理解和记忆，其关键是要熟悉并查集算法。毕竟树是不能包含环的，因此查并集在此处的应用就是：保证生成的那玩意是棵树（不包含环）。
最小生成树，就是图中若干边的集合（我们后文称这个集合为mst，最小生成树的英文缩写），你要保证这些边：

1. 包含图中的所有节点。
2. 形成的结构是树结构（即不存在环）
3. 权重和最小。

而前两点很容易通过连通集来完成，而第三点，我们打算通过利用贪心来完成。将所有边按照权重从小到大排序，从权重最小的边开始遍历，如果这条边和mst中的其它边不会形成环，则这条边是最小生成树的一部分，将它加入mst集合；否则，这条边不是最小生成树的一部分，不要把它加入mst集合。就这么简单，也就是说就是与查并集相结合来完成最小生成树。

例题应用及其步骤

【步骤】就是相比一般的查并集，多加个记录权重的变量，然后先排序，之后再查并集（记得在连接函数那里，如果成功连接了就记录下来所需要加上的权重）！

class Solution {
public:
    int count;//用来检查最后能否连接在一起
    vector<int> parent;
    int ans = 0;//用来连接时统计成本
    int minimumCost(int n, vector<vector<int>>& connections) {
        //初始化查并集
        parent.resize(n);
        for(int i=0;i<n;++i) parent[i] = i;
        count = n;
        //贪心原则-排序权重边
        sort(connections.begin(),connections.end(),[](const auto &u,const auto &k){return u[2]<k[2];});
        for(auto connection:connections)
        {
            link(connection[0]-1,connection[1]-1,connection[2]);
        }
        if(count == 1) return ans;
        return -1;

    }
    int find(int x)
    {
        if(x != parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }
    void link(int x,int y, int val)
    {
        int p_x = find(x);
        int p_y = find(y);
        if(p_x == p_y) return;
        parent[p_x] = p_y;
        count--;
        //连接了就统计上其边上的成本 
        ans+=val;//新增
    }
};

Prim最小生成树算法–优先队列+带visited的BFS

首先，Prim 算法也使用贪心思想来让生成树的权重尽可能小，也就是「切分定理」，这个后文会详细解释。
其次，Prim 算法使用 BFS 算法思想 和 visited 布尔数组避免成环，来保证选出来的边最终形成的一定是一棵树。
Prim 算法不需要事先对所有边排序，而是利用优先级队列动态实现排序的效果，所以我觉得 Prim 算法类似于 Kruskal 的动态过程。

切分定理

首先要明白切分的定义：只要你能一刀把节点分成两部分就行。所以引出原理：对于任意一种「切分」，其中权重最小的那条「横切边」一定是构成最小生成树的一条边。

有了这个切分定理，你大概就有了一个计算最小生成树的算法思路了：
既然每一次「切分」一定可以找到最小生成树中的一条边，那我就随便切呗，每次都把权重最小的「横切边」拿出来加入最小生成树，直到把构成最小生成树的所有边都切出来为止。那么如何让计算机来随意的切呢？

Prim 算法的逻辑就是这样，每次切分都能找到最小生成树的一条边，然后又可以进行新一轮切分，直到找到最小生成树的所有边为止。
当我知道了节点 A, B 的所有「横切边」（不妨表示为 cut({A, B})），也就是图中蓝色的边：

然而，在上面的图中，其cut({A, B}) 的横切边和 cut({C}) 的横切边中 BC 边重复了。所以需要用一个布尔数组visited辅助，防止重复计算横切边就行了。
最后，我们求横切边的目的是找权重最小的横切边，因此，我们就要用一个优先级队列存储这些横切边，就可以动态计算权重最小的横切边了。

代码直接详见例题吧！这里就补充一个如何判断最小生成树是否包含图中的所有节点

    bool allConnected() {
        for (int i = 0; i < visited.size(); i++) {
            if (!visited[i]) {
                return false;
            }
        }
        return true;
    }
}

例题应用及其步骤

【步骤】
1、因为用到了优先队列，因此为了方便排序，要建立vector>>类型的邻接表形式，其第一维为form，第二维是weight&to(注意，weight在前，to在后，这样优先队列省去重写()运算符的麻烦)。
2、定义好所需的visited数组（专门记录收录了哪些节点）和优先队列(最小堆)。
3、【切函数】传进来一个节点，其实就是遍历该节点的所有邻点(to)，通过visited判断是否已经访问过邻边，没有则将邻点加入优先队列。（因为有最小堆，所以往死里加就行）
4、【主函数】和BFS一样，先cut进初始的一个节点，同时将其的visited置零，随后while循环优先队列
5、先取出点来，接下来继续判断能不能放邻点。若取出来的节点其to的点被访问过，就跳过。否则就符合加进去的条件，更新visited、将其cut、并将其两点的权重加入ans总权重中。

class Solution {
public:
    int minCostConnectPoints(vector<vector<int>>& points) {
        //初始化图的邻接表表示法[from]pair（weight，int）--因为涉及大小堆，其比较第一个值
        int n = points.size();
        vector<vector<pair<int,int>>> edges;
        edges.resize(n);
        visited.resize(n,false);
        for(int i = 0;i<n;i++)
        {
            for(int j = 0;j<n;j++)
            {
                if(i == j) continue;
                int val = abs(points[i][0] - points[j][0]) + abs(points[i][1] - points[j][1]);
                edges[i].push_back({val,j});
            }
        }
        //下面是prim算法的开始
        //1、先放进去一个
        visited[0] = true;
        cut(0,edges);
        // 2、不断进行切分，向最小生成树中添加边
        while(!pq.empty())
        {
            auto cur = pq.top();
            pq.pop();
             // 节点 to 已经在最小生成树中，跳过
             // 否则这条边会产生环
            if(visited[cur.second]) continue;
             // 节点 to 加入后，进行新一轮切分，会产生更多横切边
            visited[cur.second] = true;
            cut(cur.second,edges);
            // 将边 edge 加入最小生成树
            ans += cur.first;
        }
        return ans;
    }
private:
	// 核心数据结构，存储「横切边」的优先级队列
    priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>> pq;
    // 类似 visited 数组的作用，记录哪些节点已经成为最小生成树的一部分
    vector<bool> visited;
    int ans = 0;// 记录最小生成树的权重和
    void cut(int x,vector<vector<pair<int,int>>> &edges)
    {
        for(auto edge:edges[x])
        {
            int to = edge.second;
            // 相邻接点 to 已经在最小生成树中，跳过
            // 否则这条边会产生环
            if(visited[to]) continue;
            pq.push(edge);
        }
    }
};