JavaSE 栈和队列
目录
- 1 栈 Stack
-
- 1.1 概念
- 1.2 实现
- 1.3 Stack常见方法的使用
- 1.4 前、中、后缀表达式
- 2 队列 Queue
-
- 2.1 概念
- 2.2 实现
- 2.3 循环队列
- 2.4 双端队列
- 3 Java中的栈和队列
- 4 练习题
-
- 4.1 括号匹配问题
- 4.2 用队列实现栈
- 4.3 用栈实现队列
- 4.4 实现一个最小栈
- 4.5 设计循环队列
1 栈 Stack
1.1 概念
栈: 一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则,即先进后出原则。
压栈: 栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈: 栈的删除操作叫做出栈。出数据在栈顶。

1.2 实现
- 利用顺序表实现,即使用尾插 + 尾删的方式实现。
- 利用链表实现,则头尾皆可。
相对来说,顺序表的实现上要更为简单一些,所以我们优先用顺序表实现栈。具体实现代码如下所示:
MyStack.java
/*
* 类加载器:加载类的时候,不同的类加载器加载对应的类。
* 双亲委派模型
* 3个
* */
public class MyStack {
private int[] elem;
private int top;//既可以代表下标:这个位置就是当前可以存放数据的下标
// 也可以代表当前有多少个元素
public MyStack(){
this.elem = new int[10];
}
public boolean isFull(){
return this.top == this.elem.length;
}
public int push(int item){
if(isFull()){
//return -1;
throw new RuntimeException("栈为满");
}
this.elem[this.top] = item;
this.top++;
return this.elem[this.top-1];
}
//弹出栈顶元素,并且删除
public int pop(){
if(empty()){
//return -1;
throw new RuntimeException("栈为空");
}
this.top--;
return this.elem[this.top];
}
//拿到栈顶元素不删除
public int peek(){
if(empty()){
//return -1;
throw new RuntimeException("栈为空");
}
return this.elem[this.top-1];
}
public boolean empty(){
return this.top == 0;
//return size() == 0;
}
public int size(){
return this.top;
}
}
TestDemo.java
public class TestDemo {
public static void main(String[] args) {
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.push(3);
myStack.push(1);
myStack.push(2);
myStack.push(3);
System.out.println(myStack.peek());//3
System.out.println(myStack.pop());//3
System.out.println(myStack.peek());//2
System.out.println(myStack.pop());//2
System.out.println(myStack.pop());//1
System.out.println(myStack.empty());//false
System.out.println(myStack.pop());//3
}}
但如果我们要用链表实现栈,那么入栈是头插好还是尾插好?
答案当然是头插好,因为头插法我们入栈和出栈时的时间复杂度都是1,即O(1),而尾插法我们入栈和出栈时的时间复杂度都是n,即O(n),所以头插法更好一些。
1.3 Stack常见方法的使用
具体代码示例如下所示:
package Generic;
import java.util.*;
public class TestDemo2 {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
//stack.peek() 拿到栈顶元素,但不是删除
System.out.println(stack.peek());//3
//stack.pop() 弹出栈顶元素
System.out.println(stack.pop());//3
System.out.println(stack.peek());//2
System.out.println(stack.pop());//2
System.out.println(stack.pop());//1
System.out.println(stack.empty());//true
System.out.println(stack.isEmpty());//true
//System.out.println(stack.pop());
}}
1.4 前、中、后缀表达式
前缀和后缀表达式都是没有括号的表达式。
前缀: 就是把运算符移到括号前面。
后缀: 就是把运算符移到括号后面。
经常在选择题中出现的一道题,中缀表达式如何转后缀表达式(逆波兰式)?例如我们如何将A+B*(C-(D+F)) /E这个中缀表达式转成后缀表达式?
解:(1)我们在运算过程中依旧遵循“先乘除后加减”的原则给A+B*(C-(D+F)) /E这个中缀表达式带上所有运算步骤的括号,最后得到的结果是(A+((B*(C-(D+F))) /E))。
(2)根据后缀表达式规则将运算符移到所对应括号后面,得到的结果是(A((B(C(DF)+)-)*E)/)+。
(3)将所有括号去掉得到最终结果 ABCDF+ - *E/+。
具体解题过程如下图所示:
计算机一般,对计算前缀和后缀表达式比较容易。
如何解释这句话呢?例如1+2*(4-(1+2))/2 这个中缀表达式转为后缀表达式则就是12412+ - *2/+,我们此时此时如果遇到的只要是数字则把数字依次放入栈中,遇到符号则把栈顶两个数字弹出,先弹出的数字是符号的右操作符,下一个弹出的则是符号的左操作符,将运算结果又放入栈中,依次循环直到整个表达式运算结束。具体过程可借助下图进行理解:
2 队列 Queue
2.1 概念
队列: 只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 的原则,即队尾进,队头出。
入队列: 进行插入操作的一端称为队尾(Tail/Rear)。
出队列: 进行删除操作的一端称为队头(Head/Front)。
优先级队列(PriorityQueue): 底层是二叉树来存储元素,但具备队列的特性。
双端队列(Deque): 底层是双向链表,但也具备队列的特性。
2.2 实现
队列也可以用数组和链表的结构实现,使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。我们可以借助下图对利用单链表实现队列时的尾插头删法进行一个理解:
用单链表实现一个队列的具体实现代码如下所示:
MyQueue.java
package queuedemo;
/*
* 用一个单链表实现的尾插和头删队列,时间复杂度都为1,即O(1)。
* 用一个单链表实现的头插插和尾删队列,头插时间复杂度依旧为1,即O(1);而尾删时间复杂度为n,即O(n)。
* 所以单链表实现时一般用的都是尾插头删法。
* 下面这部分是用单链表实现的一个队列
* */
class Node{
public int val;
public Node next;
public Node(int val){
this.val = val;
}
}
public class MyQueue {
public Node first;//头
public Node last;//尾
//添加元素
public boolean offer(int val){
Node node = new Node(val);
if(this.first == null){
this.first = node;
this.last = node;
}else{
this.last.next = node;
this.last = node;
}
return true;
}
//弹出元素
public int poll() throws RuntimeException {
if(isEmpty()){
throw new RuntimeException("队列为空");
}
int ret = this.first.val;
this.first = this.first.next;
return ret;
}
//拿到队头元素,但不删除
public int peek() throws RuntimeException {
if(isEmpty()){
throw new RuntimeException("队列为空");
}
return this.first.val;
}
//判断目前队列(也就是这里的链表)是否为空
public boolean isEmpty(){
if(this.last==null && this.first==null){
return true;
}
return false;
}
}
TestQueue.java
package queuedemo;
public class TestQueue {
public static void main(String[] args) {
MyQueue myQueue = new MyQueue();
myQueue.offer(1);
myQueue.offer(2);
myQueue.offer(3);
System.out.println(myQueue.peek());
System.out.println(myQueue.poll());
}
}
2.3 循环队列
2.2节我们提到过,使用数组的结构,出队列在数组头上出数据,效率会比较低,但其实实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列通常使用数组实现,环形队列如下图所示:

但在利用数组实现循环队列(又名环形队列)时,我们会遇到如下图所示的两个问题:
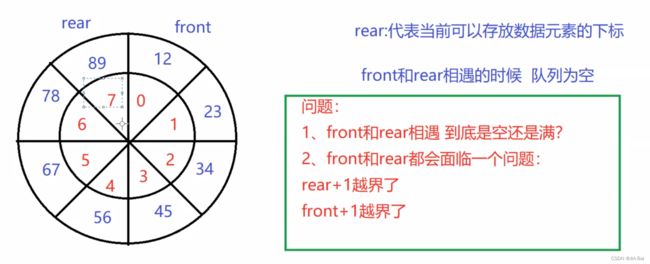
问题一: front和rear相遇时,队列到底是空还是满?
解:这个时候我们通常牺牲一个空间来判断队列是否是满的,即判断当前rear的下一个是否是front。具体可借助下图进行理解:
问题二: front和rear都会面临加1越界问题,即当前rear或front指向标号为7的位置时,我们对其进行加1操作,它们怎么指向标号为0的位置呢?
解:我们通常会利用式子:(rear +1)% len == front 来进行解决这个问题。例如:(7+1)% 8 = 0。
数组下标循环的小技巧:
- 下标最后再往后(offset 小于 array.length): index = (index + offset) % array.length。具体可借助下图进行理解:
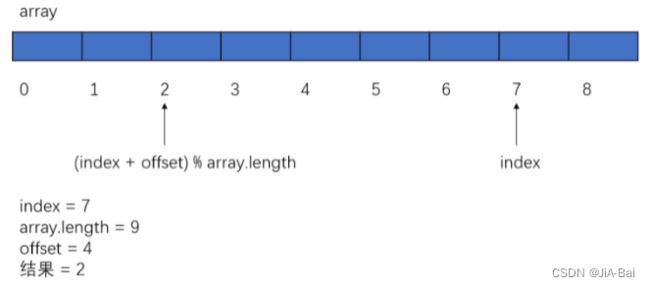
- 下标最前再往前(offset 小于 array.length): index = (index + array.length - offset) % array.length。具体可借助下图进行理解:

用数组设计实现一个循环队列的题目链接为:https://leetcode.cn/problems/design-circular-queue/。具体实现代码如下所示:
package queuedemo;
public class MyCircularQueue {
private int front;
private int rear;//代表当前存放数据元素的下标
private int[] elem;
public MyCircularQueue(int k) {
this.elem = new int[k+1];
this.front = 0;
this.rear = 0;
}
//入队
public boolean enQueue(int value) {
if(isFull()){
return false;
}
//放到数组的rear下标,rear往后走
this.elem[this.rear] = value;
this.rear = (this.rear+1) % this.elem.length;
return true;
}
//出队
public boolean deQueue() {
if(isEmpty()){
return false;
}
//只需要挪动front这个下标就好了
this.front = (this.front+1) % this.elem.length;
return true;
}
//得到队头元素
public int Front() {
if(isEmpty()){
return -1;
}
int ret = this.elem[this.front];
return ret;
}
//得到队尾元素
public int Rear() {
if(isEmpty()){
return -1;
}
int index = -1;
if(this.rear == 0){
index = this.elem.length-1;
}else{
index = this.rear-1;
}
return this.elem[index];
}
//判断队列是否为空
public boolean isEmpty() {
return this.front == this.rear;
}
//判断队列是否为满
public boolean isFull() {
return (this.rear+1)%this.elem.length == this.front;
}
}
2.4 双端队列
双端队列(deque)是指允许两端都可以进行入队和出队操作的队列,deque 是 “double ended queue” 的简称。那就说明元素可以从队头出队和入队,也可以从队尾出队和入队。
3 Java中的栈和队列
| 方法 | 解释 |
|---|---|
| E push(E item) | 压栈 |
| E pop() | 出栈 |
| E peek() | 查看栈顶元素 |
| boolean empty() | 判断栈是否为空 |
Queue:
| 错误处理 | 抛出异常 | 返回特殊值 |
|---|---|---|
| 入队列 | add(e) | offer(e) |
| 出队列 | remove() | poll() |
| 队首元素 | element() | peek() |
Deque:
| 头部/尾部 | 头部元素(队首 | 尾部元素(队尾) | ||
|---|---|---|---|---|
| 错误处理 | 抛出异常 | 返回特殊值 | 抛出异常 | 返回特殊值 |
| 入队列 | addFirst(e) | offerFirst(e) | addLast(e) | offerLast(e) |
| 出队列 | removeFirst() | pollFirst() | removeLast() | pollLast() |
| 获取元素 | getFirst() | peekFirst() | getLast() | peekLast() |
4 练习题
4.1 括号匹配问题
题目链接为:https://leetcode.cn/problems/valid-parentheses/
解题思路:
考虑把左括号放进栈中去,如果遇到右括号,则拿到栈顶元素,看栈顶元素是否和当前的字符(右括号)匹配,如果匹配,当前栈顶元素出栈,最后看栈是否为空即可判断出字符串是否有效。
具体实现代码如下所示(同时注意在牛客网写代码时要import包,但力扣不用导包):
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i = 0;i < s.length();i++){
char ch = s.charAt(i);
if(ch == '(' || ch == '[' || ch == '{'){
//说明当前遍历到的字符是左括号
stack.push(ch);
}else{
//1、判断当前的栈是否是空的
if(stack.empty()){
System.out.println("右括号多");
return false;//代表右括号多
}
//2、拿到栈顶元素,看栈顶元素是否和当前的字符匹配,如果匹配当前栈顶元素出栈
char topch = stack.peek();
if(topch == '{' && ch == '}' || topch == '[' && ch == ']' || topch == '(' && ch == ')'){
stack.pop();
}else{
System.out.println("左右括号不匹配");
return false;//代表左右括号不匹配
}
}
}
if(!stack.empty()){
System.out.println("左括号多");
return false;//代表左括号多
}
return true;
}
}
4.2 用队列实现栈
题目链接为:https://leetcode.cn/problems/implement-stack-using-queues/
具体实现代码如下所示:
class MyStack {
private Queue<Integer> qu1 = new LinkedList<>();
private Queue<Integer> qu2 = new LinkedList<>();
public MyStack() {
}
public void push(int x) {
//谁不为空入到哪个队列当中
if(!qu1.isEmpty()){
qu1.offer(x);
}else if(!qu2.isEmpty()){
qu2.offer(x);
}else{
qu1.offer(x);//指定存放到了qu1
}
}
public int pop() {
if(empty()){
return -1;
}
//每次出不为空的队列,出size-1个到另外一个为空的队列,最后弹出剩余的那一个元素
if(!qu1.isEmpty()){
int size = qu1.size();
for(int i = 0;i < size -1;i++){
qu2.offer(qu1.poll());
}
return qu1.poll();
}else{
int size = qu2.size();
for(int i = 0;i < size -1;i++){
qu1.offer(qu2.poll());
}
return qu2.poll();
}
public int top() {
if(empty()){
return -1;
}
//每次出不为空的队列,出size-1个到另外一个为空的队列,最后弹出剩余的那一个元素
if(!qu1.isEmpty()){
int size = qu1.size();
int cur = -1;
for(int i = 0;i < size;i++){
cur = qu1.poll();
qu2.offer(cur);
}
return cur;
}else{
int size = qu2.size();
int cur = -1;
for(int i = 0;i < size;i++){
cur = qu2.poll();
qu1.offer(cur);
}
return cur;
}
//这个函数是两个队列都为空
public boolean empty() {
return qu1.isEmpty() && qu1.isEmpty();
}
}
这里我们用的是两个队列实现栈,其实用一个队列实现栈也是可以实现的,即使用LinkedList双端队列进行实现。如果在笔试中我们为了赶时间,则可以使用LinkedList进行实现;如果是面试中,我们需要问一下出题者是否可以使用LinkedList来进行实现,如果出题者不允许,我们就要用两个队列实现栈这个方法了。
4.3 用栈实现队列
题目链接为:https://leetcode.cn/problems/implement-queue-using-stacks/
具体实现代码如下所示:
class MyQueue {
private Stack<Integer> s1 = new Stack<>();//入队
private Stack<Integer> s2 = new Stack<>();//出队
public MyQueue() {
}
public void push(int x) {
s1.push(x);
}
public int pop() {
//两种情况:
//1、s2为空的时候,导入全部的s1元素,弹出s2的栈顶元素
//2、s2不为空,直接弹出栈顶元素
if(empty()){
return -1;
}
if(s2.empty()){
while(!s1.empty()){
s2.push(s1.pop());
}
}
if(s2.empty(){
return -1;
}
return s2.pop();
}
public int peek() {
if(empty()){
return -1;
}
if(s2.empty()){
while(!s1.empty()){
s2.push(s1.pop());
}
}
if(s2.empty(){
return -1;
}
return s2.peek();
}
public boolean empty() {
return s1.empty() && s2.empty();
}
}
4.4 实现一个最小栈
题目链接为:https://leetcode.cn/problems/min-stack/
注意: 题目中的常数时间意思就是O(1)。
具体实现代码如下所示:
class MinStack {
private Stack<Integer> s1 = new Stack<>();
private Stack<Integer> minStack = new Stack<>();
public MinStack() {
}
public void push(int val) {
s1.push(x);
if(minStack.empty()){
minStack.push(x);
}else{
if(x <= minStack.peek()){
minStack.push(x);
}
}
}
public void pop() {
int x = s1.pop();
if(x == minStack.peek()){
minStack.pop();
}
}
//这个和最小栈没有关系
public int top() {
return s1.peek();
}
public int getMin() {
return minStack.peek();
}
}
4.5 设计循环队列
该题目就是前面2.3节当中的用数组设计实现一个循环队列,具体解题代码也在前面2.3节当中可以查看。
