浅谈AVL树
文章目录
- 1.介绍
-
- 1.1定义
- 1.2来源
- 1.3概念
-
- 1.特性
- 2.平衡因子[ Balance Factor-- _bf ]
- 2.BST==>AVL
-
- 1.示例分析
- 2.情况分类
- 3.代码剖析
-
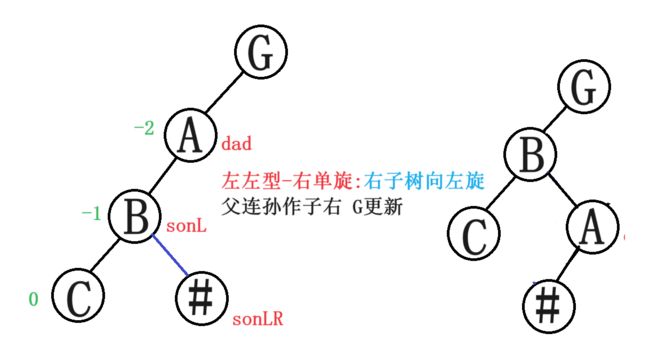
- 3.1左左型-右单旋
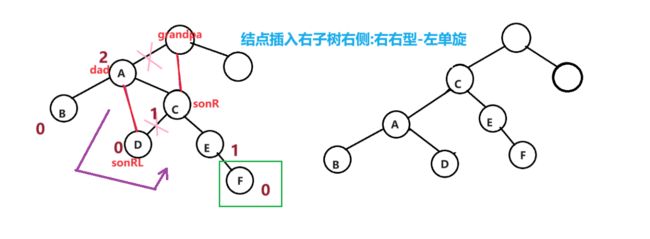
- 3.2右右型-左单旋
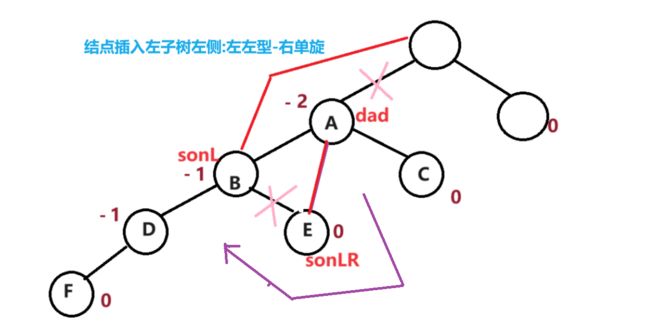
- 3.3左右型-左右旋
- 3.4右左型:右左旋
- 3.5总图
- 3.完整代码
-
- 3.1AVLTree.h
- 3.2Test.cpp
1.介绍
1.1定义
AVL树 – 平衡二叉树 – 平衡二叉搜索(排序)树 – 高度平衡搜索树
Balanced Binary Tree (BBT)
1.2来源
AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
二叉搜索树可以缩短查找的效率,但在数据有序或接近有序时它将退化为单支树,查找元素相当于在顺序表中搜索,效率低下。两位俄罗斯的数学家发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
1.3概念
1.特性
- 一棵空树或左右两个子树高度差绝对值不超过1
- 左右两个子树也都是一棵高度平衡搜索树
2.平衡因子[ Balance Factor-- _bf ]
2.BST==>AVL
[设定 _bf = 右子树高度 - 左子树高度]
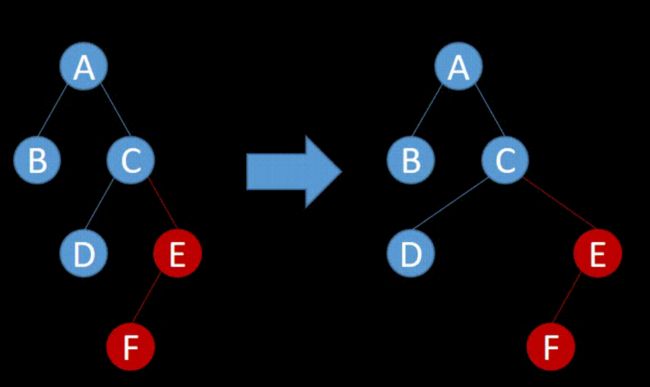
1.示例分析
先看一下下面的图 了解一下什么叫做旋转 以及旋转的目的
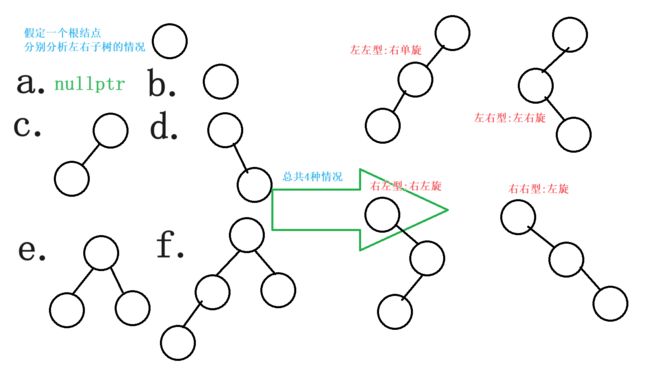
2.情况分类
3.代码剖析
3.1左左型-右单旋
void RotateRight(Node* dad)
{
Node* Grandpa = dad->_parent;
Node* sonL = dad->_left;
Node* sonLR = sonL->_right;
//dad连接sonLR sonLR不空-继承dad 为空不继承
dad->_left = sonLR;
if (sonLR)
sonLR->_parent = dad;
//sonL连接dad dad继承sonL
sonL->_right = dad;
dad->_parent = sonL;
//G为空 表明dad为根结点
if (Grandpa == nullptr)
{
//更新根结点
_root = sonL;
//更新根结点成员属性
_root->_parent = nullptr;
}
else
{
//父连子
if (Grandpa->_left == dad)
Grandpa->_left = sonL;
else
Grandpa->_right = sonL;
//子继承父
sonL->_parent = Grandpa;
}
//更新_bf
sonL->_bf = dad->_bf = 0;
}
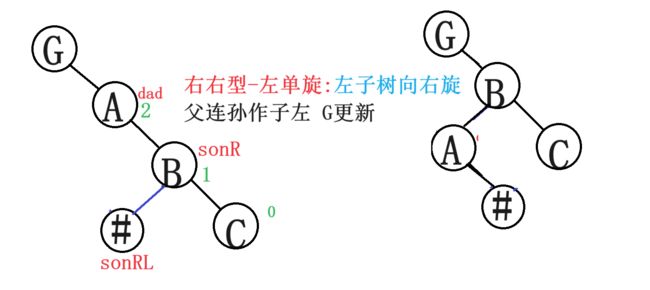
3.2右右型-左单旋
void RotateLeft(Node* dad)
{
Node* Grandpa = dad->_parent;
Node* sonR = dad->_right;
Node* sonRL = sonR->_left;
//dad连接sonRL sonRL不空继承dad 为空不继承
dad->_right = sonRL;
if (sonRL)
sonRL->_parent = dad;
//sonR连接dad dad继承sonR
sonR->_left = dad;
dad->_parent = sonR;
//Grandpa为空--dad为根节点 更新后 sonR为根节点 根节点的_parent置空
if (Grandpa == nullptr)
{
_root = sonR;
_root->_parent = nullptr;
}
//不为空 依实际连接
else
{
//父连子
if (Grandpa->_left == dad)
Grandpa->_left = sonR;
else
Grandpa->_right = sonR;
//子继承父
sonR->_parent = Grandpa;
}
//左旋目的达到 更新_bf
dad->_bf = sonR->_bf = 0;
}
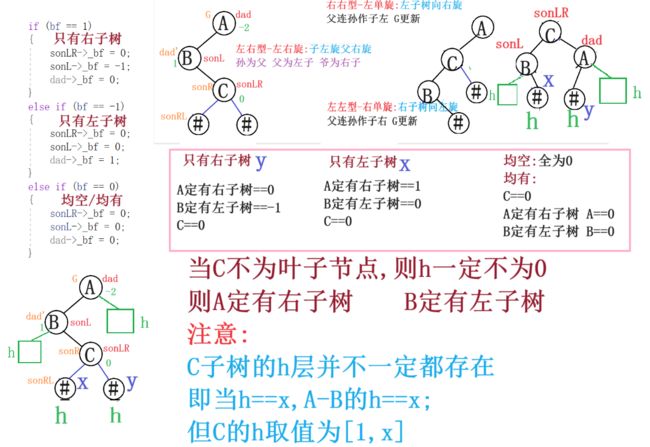
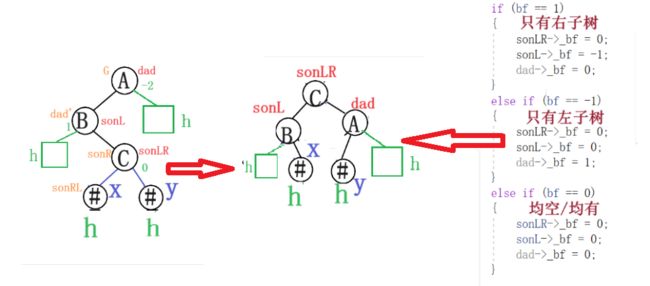
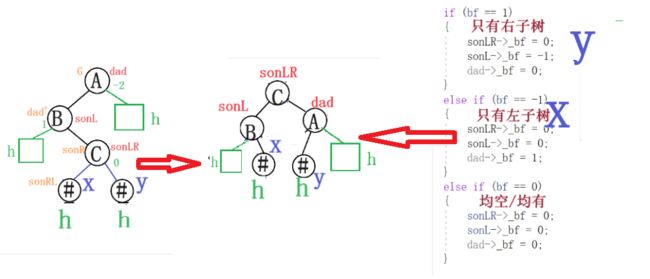
3.3左右型-左右旋
void RotateLR(Node* dad)
{
Node* sonL = dad->_left;
Node* sonLR = sonL->_right;
int bf = sonLR->_bf;
RotateLeft(sonL);
RotateRight(dad);
if (bf == 1)
{
sonLR->_bf = 0;
sonL->_bf = -1;
dad->_bf = 0;
}
else if (bf == -1)
{
sonLR->_bf = 0;
sonL->_bf = 0;
dad->_bf = 1;
}
else if (bf == 0)
{
sonLR->_bf = 0;
sonL->_bf = 0;
dad->_bf = 0;
}
else
{
assert(false);
}
}
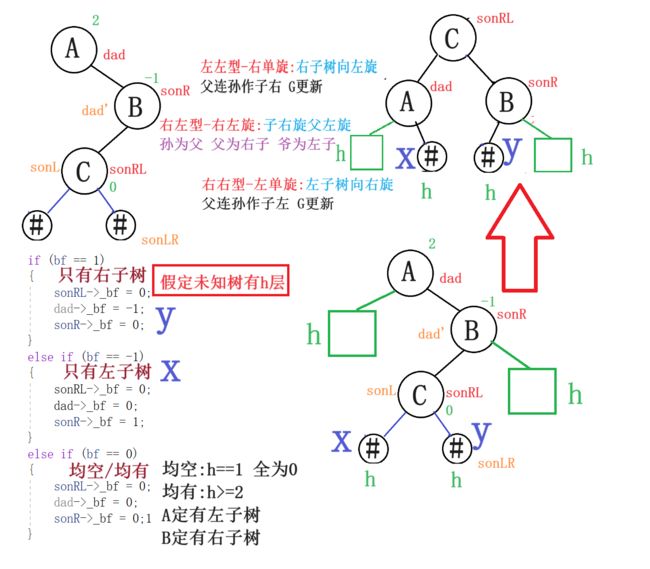
3.4右左型:右左旋
void RotateRL(Node* dad)
{
Node* sonR = dad->_right;
Node* sonRL = sonR->_left;
int bf = sonRL->_bf;//最终根结点的_bf
RotateLeft(dad->_right);
RotateRight(dad);
if (bf == 1)
{
sonRL->_bf = 0;
dad->_bf = -1;
sonR->_bf = 0;
}
else if (bf == -1)
{
sonRL->_bf = 0;
dad->_bf = 0;
sonR->_bf = 1;
}
else if (bf == 0)
{
sonRL->_bf = 0;
dad->_bf = 0;
sonR->_bf = 0;1
}
else
{
assert(false);
}
}
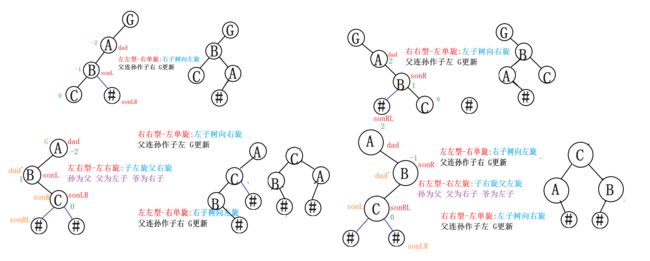
3.5总图
3.完整代码
3.1AVLTree.h
#pragma once
#include
#include 3.2Test.cpp
#define _CRT_SECURE_NO_WARNINGS
#include
#include