leetcode——回溯法

17. 电话号码的字母组合

题目：给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:
输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序

--------------------------------------------------------------------------------------------------

思路：将各个数字想象成某一位置的节点，其对应的各个字母则是该节点的子节点

    String[] strArr = {    
            "abc", 
            "def",  
            "ghi",  
            "jkl",  
            "mno", 
            "pqrs", 
            "tuv",  
            "wxyz"
    };
    List res;
    public List letterCombinations(String digits) {
      res = new ArrayList<>();
      if(digits.length() == 0) {
        return res;
      }
       fun(digits, 0, new StringBuilder());
       return res;
    }
    /*
        curIndex对应数字字符串里的数字字符，i变量循环遍历当前数字对应的各个字母字符
        curStr表示当前各个数字组成的字符串
    */
    void fun(String digits, int curIndex, StringBuilder curStr) {
        if(curIndex == digits.length()) {
          res.add(curStr.toString());
          return;
        }
        char ch = digits.charAt(curIndex);
        String letters = strArr[ch - '0' - 2];
        for(int i = 0; i < letters.length(); i++) {
          curStr.append(letters.charAt(i));
          fun(digits, curIndex + 1, curStr);
          curStr.deleteCharAt(curStr.length() - 1);
        }
    }

 

---

22. 括号生成

题目：数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

输入：n = 3
输出：[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]

--------------------------------------------------------------------------------------------------

思路：定义一个记录当前左括号数量leftCnt和当前右括号数量rightCnt。想象成一个二叉树，向左尝试即为加上'('的字符串，右向右尝试即为加上')'的字符串。不断向左和向右试探，如果右括号数量大于左括号数量 或者 左右括号数量有一个超过n值，则返回。

   public List generateParenthesis(int n) {
        List res = new ArrayList<>();
        dfs(res, "", 0, 0, n);
        return res;
    }

    void dfs(List res, String path, int leftCnt, int rightCnt, int n) {
      if(leftCnt == rightCnt && leftCnt == n) {
        res.add(path);
        return;
      }
      if(leftCnt < n)
        dfs(res, path + '(', leftCnt + 1, rightCnt, n);
      if(rightCnt < leftCnt)
      dfs(res, path + ')', leftCnt, rightCnt + 1, n);
    }

 

---

46. 全排列

题目：给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

--------------------------------------------------------------------------------------------------

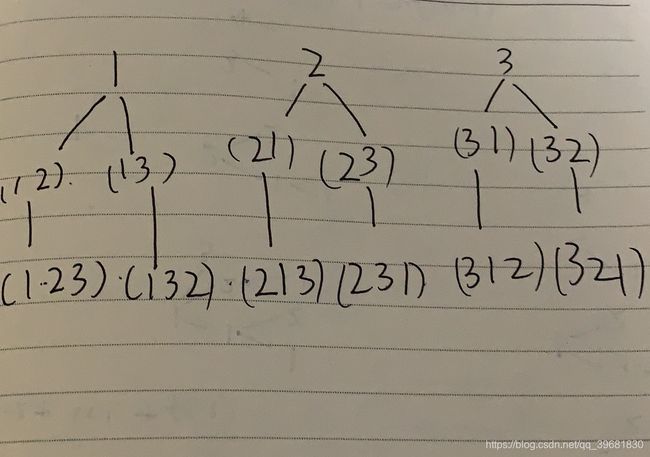
思路：对于数1，它有2，3两个数字可选：对于（12）则只有选择3；对于（13）则只有选择2。其他两个数也是类似的道理。

   List> res = new LinkedList<>();

    public List> permute(int[] nums) {
      createTree(nums, new LinkedList());
      return res;
    }

    void createTree(int[] nums, LinkedList path) {
      if(path.size() == nums.length) {
        res.add(new LinkedList(path));
        return;
      }
      for(int i = 0; i < nums.length; i++) {
        if(path.contains(nums[i]) != true) {
          path.add(nums[i]);
          createTree(nums, path);
          path.removeLast();
        }
      }
    }

 

---