BAW美式期权定价半解析解
BAW美式期权定价半解析解
参考文献:G. Barone-Adesi & R. E. Whaley, Efficient Analytic Approximation of American Option Values, The Journal of Finance, No 2 (June 1987), 301-320
基本思想:美式期权不同于欧式期权之处在于,美式期权可以在到期日之前随时执行,因而美式期权的价值高于欧式期权。美式期权价值高于欧式期权的部分叫做美式期权溢价 ϵ c \epsilon_c ϵc,如下式所示:
ϵ c ( S , T ) = C ( S , T ) − c ( S , T ) , \epsilon_c\left( S , T \right) = C \left( S , T \right) -c \left( S , T \right) , ϵc(S,T)=C(S,T)−c(S,T),
其中 C ( S , T ) C \left( S , T \right) C(S,T)表示美式看涨期权的价值; c ( S , T ) c \left( S , T \right) c(S,T)表示欧式看涨期权的价值。
根据Feynman_Kac定理,在无套利假设条件下,欧式期权价值和美式期权价值满足椭圆的偏微分方程,因而,风险溢价也应该满足以下的相同形式的椭圆偏微分方程:
1 / 2 σ 2 S 2 ε S S − r ε + b S ε S + ε t = 0 (1) 1 / 2 \sigma^{2} S^{2} \varepsilon_{S S}-r \varepsilon+b S \varepsilon_{S}+\varepsilon_{t}=0\tag{1} 1/2σ2S2εSS−rε+bSεS+εt=0(1)
做如下的变量替换:
τ = T − t \tau = T -t τ=T−t 代表距离到期日T的时间;
M = 2 r / σ 2 和 N = 2 b / σ 2 M=2 r / \sigma^{2} \text { 和 } N=2 b / \sigma^{2} M=2r/σ2 和 N=2b/σ2
则式(1)可以重写为
S 2 ε S S − M e + N S e S − ( M / r ) ε τ = 0 (2) S^{2} \varepsilon_{S S}-M_{e}+N S e_{S}-(M / r)\varepsilon_{\tau}=0\tag{2} S2εSS−Me+NSeS−(M/r)ετ=0(2)
定义美式期权的提前行权溢价满足如下的形式:
ϵ c ( S , K ) = K ( τ ) f ( S , K ) \epsilon_c(S, K)=K(\tau) f(S, K) ϵc(S,K)=K(τ)f(S,K)
其中 K ( T ) = 1 − e − r τ , K \left( T \right) = 1 - e ^ { - r \tau} , K(T)=1−e−rτ, 则(2)式可以重写为
S 2 f s s + N S f s − ( M / K ) f − ( 1 − K ) M f K = 0 (3) S^{2} f s s+N S f_{s}-(M / K) f-(1-K) M f_{K}=0\tag{3} S2fss+NSfs−(M/K)f−(1−K)MfK=0(3)
敲黑板!!!BAW方法为何是半解析解,就在于我们要对式(3)进行简化,把最后一项省略掉,式(3)就可以变成一个二次常微分方程。那么最后一项为何可以省略掉呢?当商品期权距离到期日时间非常短(T=0)的时候, f K f_{K} fK接近于0,即执行价格对风险溢价几乎没影响。当商品期权距离到期日的时间非常长( τ = ∞ \tau=\infin τ=∞)的时候,K=1则1-K=0。因而, f f f可以通过近似求解以下的表达式得到:
S 2 f s s + N S f s − ( M / K ) f = 0 S^{2} f s s+N S f_{s}-(M / K) f=0 S2fss+NSfs−(M/K)f=0
假设 f = a S q f=a S^{q} f=aSq,代入上式,可以得到两个特征根(M/K为正):
q 1 = − ( N − 1 ) − ( N − 1 ) 2 + 4 M / K 2 < 0 q _ {1} = - \left( N - 1 \right) - \frac{\sqrt { \left( N - 1 \right) ^ { 2 } + 4 M / K }}{2}<0 q1=−(N−1)−2(N−1)2+4M/K<0
q 2 = − ( N − 1 ) + ( N − 1 ) 2 + 4 M / K 2 > 0 q _ {2} = - \left( N - 1 \right) + \frac{\sqrt { \left( N - 1 \right) ^ { 2 } + 4 M / K }}{2}>0 q2=−(N−1)+2(N−1)2+4M/K>0
则有通解:
f ( S ) = a 1 S q 1 + a 2 S q 2 , f \left( S \right) = a _ { 1 } S ^{ q _ { 1 } } + a _ { 2 } S ^{ q_2 } , f(S)=a1Sq1+a2Sq2,
现在的问题是如何确定参数 a 1 a_1 a1和 a 2 a_2 a2。这个问题要追溯到美式看涨期权的边值条件
∂ C ∂ S ( S ∗ , τ ) = 1 (B1) \frac{\partial C}{\partial S}(S^*,\tau)=1\tag{B1} ∂S∂C(S∗,τ)=1(B1)
C ( 0 , τ ) = 0 (B2) C(0,\tau)=0\tag{B2} C(0,τ)=0(B2)
C ( S ∗ , τ ) = S ∗ − K (B3) C(S^*,\tau)=S^*-K\tag{B3} C(S∗,τ)=S∗−K(B3)
由(B2): C ( 0 , τ ) = c ( 0 , τ ) + K ( τ ) f ( 0 ) = 0 C(0,\tau)=c(0,\tau)+K(\tau)f(0)=0 C(0,τ)=c(0,τ)+K(τ)f(0)=0, 可以推出 f ( 0 ) = 0 f(0)=0 f(0)=0,因而 f ( S ) = a 2 S q 2 ( q 1 < 0 ) f(S)=a _ { 2 } S ^{ q_2 }(q_1<0) f(S)=a2Sq2(q1<0)。
由(B1): ∂ C ∂ S ( S ∗ , τ ) = ∂ c ∂ S ( S ∗ , τ ) + K ( τ ) ∂ f ∂ S \frac{\partial C}{\partial S}(S^*,\tau)=\frac{\partial c}{\partial S}(S^*,\tau)+K(\tau)\frac{\partial f}{\partial S} ∂S∂C(S∗,τ)=∂S∂c(S∗,τ)+K(τ)∂S∂f 可以推导出
1 = e ( b − r ) τ N [ d 1 ( S ∗ ) ] + K q 2 a 2 S ∗ q 2 − 1 1=e^{(b-r) \tau} \mathrm{~N}\left[d_{1}\left(S^{*}\right)\right]+K q_{2} a_{2} S^{* q_{2}-1} 1=e(b−r)τ N[d1(S∗)]+Kq2a2S∗q2−1
这里用到了欧式期权的BS公式:
c ( S , T ) = S e ( b − r ) T N ( d 1 ) − X e − r T N ( d 2 ) c(S, T)=S e^{(b-r) T} \mathrm{~N}\left(d_{1}\right)-X e^{-r T} \mathrm{~N}\left(d_{2}\right) c(S,T)=Se(b−r)T N(d1)−Xe−rT N(d2)
其中 d 1 = [ ln ( S / X ) + ( b + 0.5 σ 2 ) T ] / σ T , d 2 = d 1 − σ T d_{1}=\left[\ln (S / X)+\left(b+0.5 \sigma^{2}\right) T\right] / \sigma \sqrt{T}, d_{2}=d_{1}-\sigma \sqrt{T} d1=[ln(S/X)+(b+0.5σ2)T]/σT,d2=d1−σT。
由此,可以求解出
a 2 = { 1 − e ( b − r ) τ N [ d 1 ( S ∗ ) ] } / K q 2 S ∗ q 2 − 1 a_{2}=\left\{1-e^{(b-r) \tau} \mathrm{~N}\left[d_{1}\left(S^{*}\right)\right]\right\} / K q_{2} S^{* q_{2}-1} a2={1−e(b−r)τ N[d1(S∗)]}/Kq2S∗q2−1
由(B3)可以求解出最优执行边界满足以下的表达式
S ∗ − X = c ( S ∗ , τ ) + { 1 − e ( b − r ) τ N [ d 1 ( S ∗ ) ] } S ∗ / q 2 S^{*}-X=c\left(S^{*}, \tau\right)+\left\{1-e^{(b-r) \tau} \mathrm{~N}\left[d_{1}\left(S^{*}\right)\right]\right\} S^{*} / q_{2} S∗−X=c(S∗,τ)+{1−e(b−r)τ N[d1(S∗)]}S∗/q2
综上所述,美式看涨期权的解析公式如下所示:
C ( S , τ ) = c ( S , τ ) + A 2 ( S / S ∗ ) q 2 , when S < S ∗ C ( S , τ ) = S − K , when S ≥ S ∗ \begin{array}{ll} C(S, \tau)=c(S, \tau)+A_{2}\left(S / S^{*}\right)^{q_{2}}, & \text { when } S
其中 A 2 = ( S ∗ / q 2 ) { 1 − e ( b − r ) T N [ d 1 ( S ∗ ) ] } A_{2}=\left(S^{*} / q_{2}\right)\left\{1-e^{(b-r) T} \mathrm{~N}\left[d_{1}\left(S^{*}\right)\right]\right\} A2=(S∗/q2){1−e(b−r)T N[d1(S∗)]}。
美式看跌期权与看涨期权的求解套路差不多:
ϵ p ( S , T ) = P ( S , T ) − p ( S , T ) \epsilon_p\left( S , T \right) = P \left( S , T \right) -p \left( S , T \right) ϵp(S,T)=P(S,T)−p(S,T)
区别在于边界条件不同
∂ P ∂ S ( S ∗ , τ ) = − 1 (B1) \frac{\partial P}{\partial S}(S^*,\tau)=-1\tag{B1} ∂S∂P(S∗,τ)=−1(B1)
P ( ∞ , τ ) = 0 (B2) P(\infin,\tau)=0\tag{B2} P(∞,τ)=0(B2)
P ( S ∗ , τ ) = K − S ∗ (B3) P(S^*,\tau)=K-S^*\tag{B3} P(S∗,τ)=K−S∗(B3)
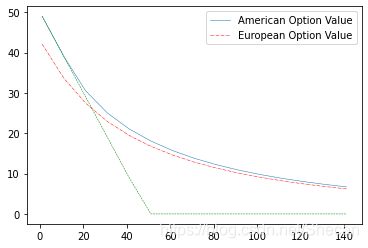
python程序实现:参考Python implementation of the Barone-Adesi And Whaley model for the valuation of American options and their greeks. · GitHub
调用实例:
from BAW import *
import matplotlib.pyplot as plt
Stock = []
Put_American = []
Put_European = []
Expir = []
K = 50
for S in range(1,151,10):
Stock.append(S)
Expir.append(max(K-S,0))
put_American = getValue('American', 'Value', 'Put', S, K, 5, 0.03, 0.02,0.5)
put_European = getValue('European', 'Value', 'Put', S, K, 5, 0.03, 0.02,0.5)
Put_American.append(put_American)
Put_European.append(put_European)
plt.plot(Stock, Put_American,linewidth=0.5,label='American Option Value')
plt.plot(Stock, Put_European,'r-.',linewidth=0.5,label='European Option Value')
plt.plot(Stock, Expir, 'g--',linewidth=0.5)
plt.legend()
plt.show()