回溯算法(例题详细解析)
日升时奋斗,日落时自省
目录
1、深度优先解题
1.1、一条到走到黑
1.2、员工的重要性
1.3、图像渲染
1.4、被围绕的区域
1.5、电话号码的字母组合
1.6、组合总和
1.7、活字印刷
1.8、N皇后
2、广度优先搜索
2.1、迷宫问题
2.2、腐烂的橘子
2.3、单词接龙
2.4、打开转盘锁
回溯不用直接去理解词名,实际上类似枚举,不断尝试各种情况,在尝试不同情况中寻找问题的解,当发现当前情况已经不满足求解需要了,就产生“回溯” 返回 (直白说就是递归条件到头了,返回),尝试别的路径
(1)回溯法是一种选优先搜索法,按选优条件向前搜索,以达到目标,但当探索到某一步时,,发现原先选择并不优或达不到目标,就回退一步重新选择(排除当前选择),这种走不通过就回退再走的技术为回溯法,而满足回溯条件的某个状态的点成为“回溯点”,也可以成为剪枝点,所谓的剪枝,指的是不必要的步骤或者路径去掉
(2)复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称
(3)在包含问题的所有解空间树中个,按照深度优先搜索的策略,从根节点出发深度探索解空间树,当探索到某一节点时,要先判断该节点是否包含问题的解,如果包含就从该节点出发,继续探索下去,如果该节点不被包含,则逐层向其祖先节点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)
(4)若用回溯法求问题的所有解时,要回溯到根,且根节点的所有可行的子树都要已被搜索遍历才结束
(5)若用回溯法求问题只有一个解,只要深度优先搜索到问题的解就可以结束了
文字叙述总显得很浅显,以下用例题详细解析 “回溯” 如何深度理解
1、深度优先解题
1.1、一条到走到黑
使用方法:深度优先搜索
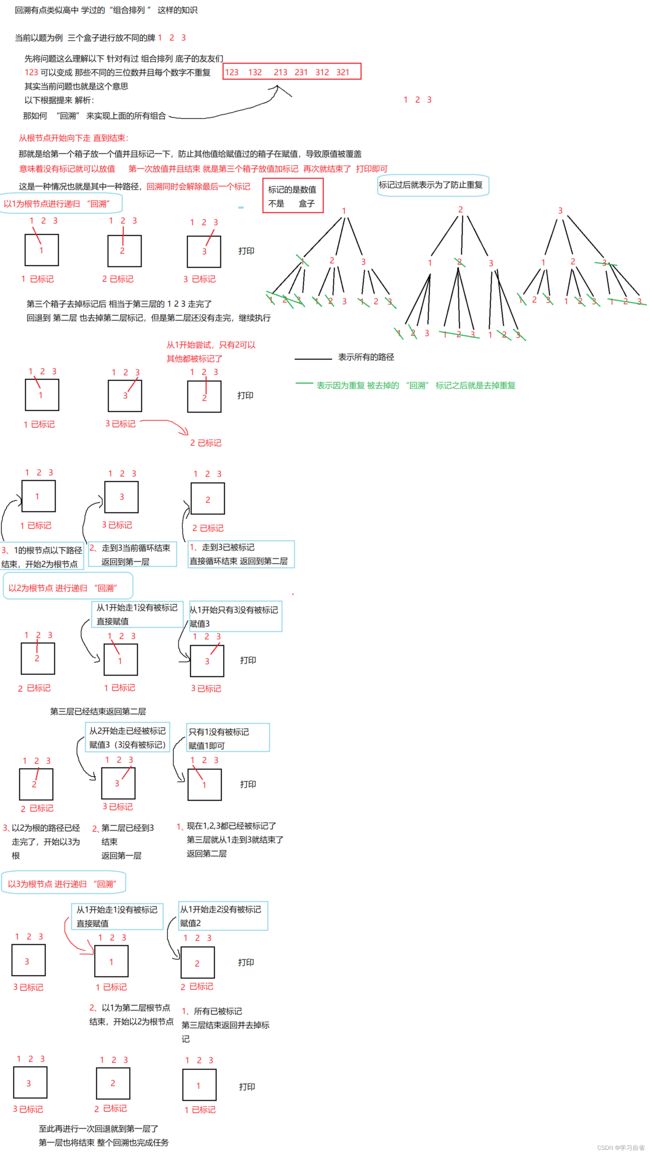
假如有编号为1~3 的3张扑克牌和编号为1~3的3个盒子,现在需要将3张牌分别放到3个盒子中去,且每个盒子只能做一张牌,一共有多少种不同的放法(图解)
代码解析(附加注释):
public static void main(String[] args) {
int n;
Scanner scanner=new Scanner(System.in);
n=scanner.nextInt();
//为什么数组要多创建一个空间 因为0下标的用不上 从1开始计数并且使用
//此处也是看需求而定
int [] boxs=new int[n+1]; //盒子
int [] books=new int[n+1]; //准备一数组标记值
Dfs(1,n,boxs,books); //深度优先遍历
}
private static void Dfs(int index, int n, int[] boxs, int[] books) {
//判定盒子是否是装满的 为啥index == n+1 因为 Dfs要多执行一次 所以index会在原有个数上多一
if(index==n+1){
//以下是为了打印 能到底层的路径
for(int i=1;i<=n;i++){
System.out.print(boxs[i]+" ");
}
System.out.println();
return ;
}
for(int i=1;i<=n;i++){
if(books[i]==0){ //第 i 号牌仍在手上 说明还没有被用,就是还没有被标记
// 把当前还没有进行标记的值 赋值给盒子
boxs[index]=i;
books[i]=1; //这个值 已经给了一个盒子,这个值就不能再用了,需要标记一下
//处理下一个盒子 下面参数 index+1 就表示下一个盒子
Dfs(index+1,n,boxs,books);
//无论什么情况回溯 都需要 将本值的标记取消,因为该值能回退,说明已经用过了
books[i]=0;
}
}
}1.2、员工的重要性
使用方法:深度优先搜索
题目源于力扣:力扣
题目描述:给定一个保存员工信息的数据结构,它包含了员工 唯一的 id ,重要度 和 直系下属的 id 。
比如,员工 1 是员工 2 的领导,员工 2 是员工 3 的领导。他们相应的重要度为 15 , 10 , 5 。那么员工1的数据结构是[1,15,[2]],员工2的数据结构是[2,10,[3]],员工3的数据结构是[3,5,[]]。(图解)
题目最终求解:所有员工重要度一共是多少(也就是所有员工重要度加起来)
代码解析(附加注释):
class Employee {
public int id; //员工号
public int importance; //该员工的重要度
public List subordinates; //存放下级员工id
};
public class GetImportanceTest {
public int getImportance(List employees,int id){
// 每次都是向下级递归 如果当前级别已经没有下级了也就是空 此处结束 回退
if(employees.isEmpty()){
return 0;
}
//以下的 Map 存放的是 的是员工的 id 和 员工的整个信息
Map info=new HashMap<>();
//存入所有的员工的信息
for(Employee e:employees){
//key存放员工 id 同时value对应员工的所有信息
info.put(e.id, e);
}
//使用DFS 实现回溯 加 每个员工的重要度
return DFS(info,id);
}
private int DFS(Map info, int id) {
//首先获得下级的id 准备向下递归
Employee cur=info.get(id);
//获取当前员工的 重要度
int curSum=cur.importance;
// 将下级进行深度优先搜索 如果没有下级就 “回溯”
for(int curd:cur.subordinates){
curSum+=DFS(info,curd);
}
return curSum;
}
} 1.3、图像渲染
使用方法:深度优先搜索
题目源于力扣:力扣
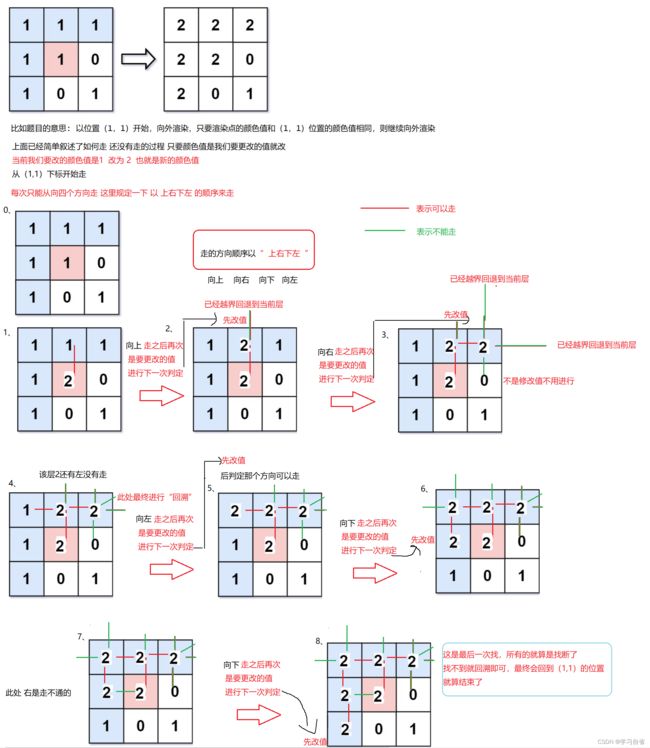
题目描述:我们照相的话知道像素,如果使用ps这样的工具把图片拉大了,能看见一小块一小块的图案带有颜色,对题的理解基本如上,如果能够实现相同点数的位置用同一种颜色 ,就是图像渲染
如何完成上色,从初识像素开始,把和初始坐标开始,颜色值相同的点的颜色全部改为新的颜色,并且只要某个点颜色被更改,则继续以此点周围渲染
代码解析(附加注释):
//图像渲染
//对应参数分别是 当前颜色值使用二维数组表示 当前颜色点的位置 行:srow 列:scol
//newColor 是新颜色位置
//四个方位 顺时针建立
int[][] nextPosition={{0,1},{1,0},{0,-1},{-1,0}}; //从左向右分别代表上右下左
public int[][] floodFill(int[][] image,int srow,int scol,int newColor){
//要知道原来的颜色是什么值
int oldColor =image[srow][scol];
//当前渲染的 行 和 列 有多大
int row=image.length; //行
int col=image[0].length; //列
//建立标记
int[][] book=new int[row][col];
//深度遍历同时 回溯
DFS(image,row,col,book,srow,scol,oldColor,newColor);
return image;
}
private void DFS(int[][] image, int row, int col, int[][] book, int srow, int scol, int oldColor, int newColor) {
// 修改当前位置的颜色 并且做已标记 ,标记表示已经修改过了
image[srow][scol]=newColor;
book[srow][scol]=1;
for(int k=0;k<4;k++){
//k 在这里是以4为限制 表示给四个方位逐一加一次
//处理行 新的行坐标
int newSrow=srow+nextPosition[k][0];
//处理列 新的列坐标
int newScol=scol+nextPosition[k][1];
//防止向四周进行越界
if(newSrow>=row||newSrow>0||newScol<0||newScol>=col){
continue;
}
//满足两个条件就可以改色了
// 第一个就是该颜色是要改的颜色
// 第二个就是该颜色没有被改过 也就就是没有被标记过
if(image[newSrow][newScol]==oldColor&&book[newSrow][newScol]!=1){
//只有进入递归才能 在下一次进行改色
DFS(image,row,col,book,newSrow,newScol,oldColor,newColor);
}
}
}1.4、被围绕的区域
使用方法:深度优先搜索
题目源于力扣:力扣
本题的意思被包围的区间不会存在于边界上,所以边界上的o以及与o联通的都不算做包围,只要把边界上的o以及yu之联通的o进行特殊处理,剩下的o替成x即可。故问题转化为,如何寻找和边界联通的o,我们需要考虑如下情况。
代码解释(附加注释):
//四个方位 移动
int[][] nextPosition={{0,1},{1,0},{0,-1},{-1,0}};
public void dfs(char[][] board,int row,int col,int i,int j){
//当前位置设为 ‘*’ 说了将边界上的o 改为特殊值 进行保存
board[i][j]='*';
for(int k=0;k<4;k++){
//向四个方向扩散
int ni=i+nextPosition[k][0];
int nj=j+nextPosition[k][1];
//判断边界
if(ni<0||ni>=row||nj<0||nj>=col){
continue;
}
//是 ‘o’ 说明和边界联通 继续搜索是否有联通的
//只要不等于 * 且不等于 X 一共只有三种标志
if(board[ni][nj]!='*'&&board[ni][nj]!='X'){
dfs(board,row,col,ni,nj);
}
}
}
public void solve(char[][] board){
if(board.length==0){
return ;
}
//寻找边上的每一个0 ,如果每一
//表示所有的0都被包围
int row =board.length;
int col =board[0].length;
//寻找第一行和最后一行
for(int j=0;j1.5、电话号码的字母组合
使用方法:深度优先搜索
题目源于力扣:力扣
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
代码解析(附加注释):
//对应不同编号的 2 - 9 电话的英文字母
String[] mapString={"","","abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
private void backTrace(String digits, List ret, StringBuilder curStr, int curDepth) {
//边界 找到一种组合 ,放入数组中,结束此路径 向上回溯
if(curDepth==digits.length()){
if(curStr.length()!=0){
ret.add(curStr.toString());
}
return ;
}
//找到当前字符在String映射表中的位置 等到对应的下标
int curMapIndex=digits.charAt(curDepth)-'0';
//对应字符串
String curMap=mapString[curMapIndex];
//遍历每一种可能的组合
for(int i=0;i letterCombination(String digits){
//用来存储不同情况的子串
List ret=new ArrayList<>();
//处理可变的字符串
StringBuilder curStr=new StringBuilder("");
//回溯位置
backTrace(digits,ret,curStr,0);
return ret;
} 1.6、组合总和
使用方法:深度优先搜索
题目源于力扣:力扣
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
此题相加的元素可以重复,所以去下一个元素的位置可以从当前位置开始,DFS+回溯为了保证组合不重复(顺序不同,元素相同,也算重复),不再从当前位置向前看
1.从第一个元素开始相加
2.让局部和继续累加候选的剩余值
3.局部和等于目标值,保存组合,向上回退,寻找其它组合
代码解析(附加注释):
public List> combinationSum(int[] candidates,int target){
//存放能够组合起来等于 target的组合
List solution=new ArrayList<>();
//存放不同情况的集合
List> solutions=new ArrayList<>();
//如果这个数组没有值的话 就找不到目标
if(candidates.length==0){
return solutions;
}
int curSum=0; //计算相加值 与 target对比
dfs(candidates,solutions,solution,curSum,0,target);
return solutions;
}
private void dfs(int[] candidates, List> solutions, List solution, int curSum, int prevPosition, int target) {
//边界,如果大于等于目标,则结束
if(curSum>=target){
//等于目标 ,找到一个组合
if(curSum==target){
List news=new ArrayList<>();
//如果值对应位置
for(int e: solution){
//需要进行拷贝
news.add(e);
}
//拷贝完成后 ,放入结果集中
solutions.add(news);
}
return ;
}
//可以从上一个位置开始 ,因为元素可以重复
for(int i=prevPosition;i< candidates.length;i++){
//单个值已经大于目标 ,直接跳过
if(candidates[i]>target){
continue;
}
//将当前 直接假如
solution.add(candidates[i]);
//继续进行可以执行重复数字
dfs(candidates,solutions,solution,curSum+candidates[i],i,target);
//回溯 向上回退 删除当前位置
solution.remove(solution.size()-1);
}
} 1.7、活字印刷
使用方法:深度优先搜索
题目源于力扣:力扣
有一套活字字模 tiles,其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。
此题组合的长度不唯一,最小组合长度为1,最大组合长度为tiles的长度
按照题意tiles中每一个位置的字符在组合中只能出现一次,所以可以用一个标记辅助
当去组合新的组合时,可以与tiles中的每一个位置组合,但是如果当前位置已经在当前组合中出现过,则跳过虽然此题中每一个位置字符在组合中只能出现一次,但是tiles中可能有相同的字符,所以需要考虑重复的组合
DFS + 回溯
1.当前组合不为空 ,则插入set中
2.继续给当前组合拼接新的组合,尝试拼接tiles每一个位置的字符
3.如果当前位置已在组合中出现过,返回到2,否则标记当前位置,继续拼接更长的组合的
4.回溯,尝试组合其它位置,返回2
当所有位置都已经使用过时,当前递归就结束了,继续向上层DFS回退(图解)
代码解析(附加注释):
public int numTilepossibilities(String tiles){
if(tiles.length()==0){
return 0;
}
//set 天生去重
Set totalString =new HashSet<>();
//标记全部初始化为未使用
List usedIndex=new ArrayList<>();
//针对 活字模板 将模板的值进行标记 为 0
for(int i=0;i usedIndex, Set totalString) {
//是以不同个数模板进行
if(curStr.length()!=0){
totalString.add(curStr.toString());
}
//标记保证所有位都用完之后 就结束了
for(int i=0;i 1.8、N皇后
使用方法:深度优先搜索
题目源于力扣:力扣
题目描述:N皇后问题:把N个皇后放值N*N的二维矩阵中,保证他们相互不能攻击:既不在同一行,同一列,同一个斜线上(三种可能情况)
思想:DFS + 回溯
从第一行开始放置皇后,每确定一个位置,判断是否会冲突:是否在同一列,同一行,或者同一斜线,当前行位置确定之后,继续确定下一行的位置回退,尝试当前行的其他位置
代码解析(附加注释):
class pair{
public int x; //横坐标
public int y; //纵坐标
public pair(int x ,int y){//传参
this.x=x;
this.y=y;
}
}
public class SolveNQueensTest {
public List> solveNQueens(int n){
//按坐标位置存放所有解决方案 存放结果集
List> solutions=new ArrayList<>();
//存放一种解决方案中的所有皇后的位置 存放结果
List solution=new ArrayList<>();
nQueensBackTrack(solutions,solution,0,n);
//把坐标位置转成String
return transResult(solutions,n);
}
private List> transResult(List> solutions, int n) {
List tmp=new ArrayList<>();
//把每一种解决方案都转换为String 形式 ,最终结果
List> ret=new ArrayList<>();
for(List solution : solutions){
//n*n char : 每行有n个元素 把皇后的位置修改为 Q
List solutionString=new ArrayList<>();
//针对每一行
for(int i=0;i curRet=new ArrayList<>();
//将所有的 集合中的每行都存放起来
for(StringBuilder sb : solutionString){
curRet.add(sb.toString());
}
//最终存储到结果集
ret.add(curRet);
}
return ret;
}
private boolean nQueensBackTrack(List> solutions, List solution, int curRow, int n) {
//如果可以话 说明当前情况已经符合条件了将符合条件进行拷贝存储
if(curRow==n){
List newS=new ArrayList<>();
//进行拷贝
for(pair p:solution){
newS.add(p);
}
//放入结果集中
solutions.add(newS);
}
//尝试当前行的每一个位置是否可以放置一个皇后
for(int col=0;col solution, int row, int col) { //判断当前行尝试的皇后位置是否和前面几行的皇后位置有冲突
// i.second == col 第i个皇后与当前这个点在同一列
// i.first+i.second =row + col 第i个皇后与当前点在反斜杠 横坐标 + 纵坐标值相同
// i.first+i.second =row - col 第i个皇后与当前点在正斜杠 横坐标 - 纵坐标值相同
for(pair i: solution){
if(i.y==col||i.x+i.y==row+col||i.x-i.y==row-col){
return false;
}
}
return true;
}
}
2、广度优先搜索
2.1、迷宫问题
使用方法:广度优先搜索
题目源于力扣:力扣
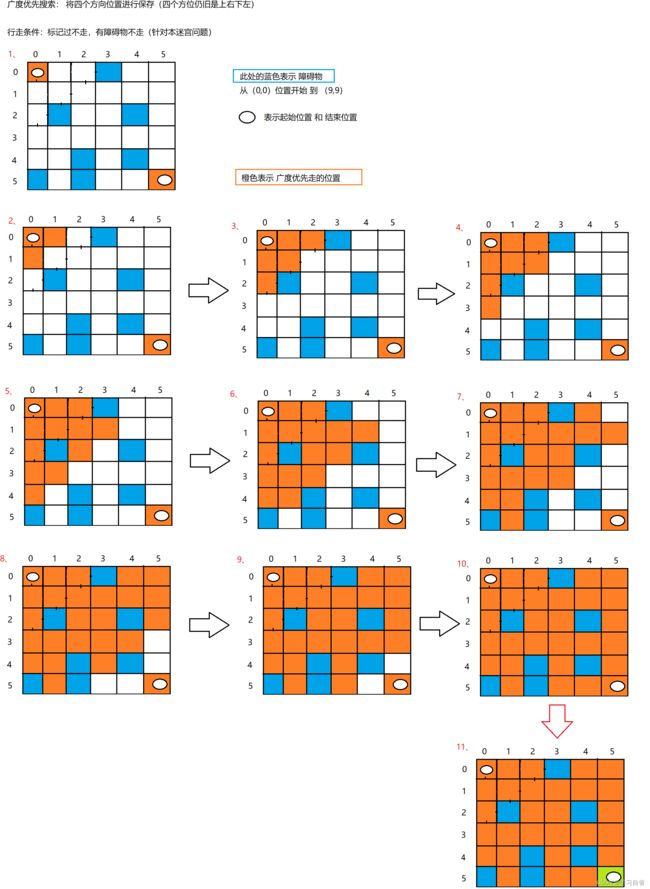
迷宫问题:假设有一个迷宫,里面有障碍物,迷宫用二维矩阵表示,标记为0的地方表示可以通过,标记为1的地方表示障碍物,不能通过。现在给一个迷宫出口,让你判断是否可以从入口进来之后,走出迷宫,每次可以向任意方向走。(图解)
代码解析(附加注释):
class node{
public int x; //节点 横坐标
public int y; //节点 纵坐标
public node(int x,int y){
this.x=x;
this.y=y;
}
}
public class MazeTest {
public static void main(String[] args) {
int sx,sy,ex,ey;
int m,n;
System.out.println("请输入迷宫的大小:行、列");
Scanner scanner=new Scanner(System.in);
m= scanner.nextInt();
n= scanner.nextInt();
//创建一个数组
int[][] graph=new int[m][n];
System.out.println("请输入迷宫的元素");
//给迷宫所有位置附加值
for(int i=0;i q=new LinkedList<>();
//标记迷宫中的位置是否被走过
int[][] book=new int[m][n];
//将当前第一个节点 放入 队列中
q.offer(new node(startx,starty));
//标记已经走过
book[startx][starty]=1;
//四个行走的方向 左右下上
int[][] next={{-1,0},{1,0},{0,-1},{0,1}};
//标记是否可以出去
boolean flag=false; //此处用来判定 是否找到最终位置
while(!q.isEmpty()){
//当前位置带出所有新的位置,可以向上下左右走
for(int i=0;i<4;i++){
//计算新的位置
int nx=q.peek().x+next[i][0];
int ny=q.peek().y+next[i][1];
//新的位置越界,继续下一个
if(nx>=m||nx<0||ny>=n||ny<0){
continue;
}
//如果新的位置无障碍并且之前也没有走过,保存新的位置
if(graph[nx][ny]==0&&book[nx][ny]==0){
q.offer(new node(nx,ny));
//标记已被走过
book[nx][ny]=1;
}
//如果新的位置为目标位置,则结果查找
if(nx==destx&&ny==desty){
flag=true;
break;
}
}
//判定为了结束外界循环
if(flag){
break;
}
//否则,用新的位置继续向后走
q.poll();
}
return flag;
}
} 2.2、腐烂的橘子
使用方法:广度优先搜索
题目源于力扣:力扣
本题可以先找到所有的腐烂橘子,入队 ,用第一批带出新一批腐烂的橘子,每一批橘子都会在一分钟之内腐烂,每一次腐烂都是一个广度优先搜索,step表示时间 ,也就是每一次广度优先搜索针对题意都会花费1分钟 step++
最后广度优先遍历结束后,再去遍历原来的给定m*n数组,还有没有新鲜橘子(判定有没有数组值是1)
注:此处就不在进行图像演示了,打开力扣题后图解已经很清晰了。
代码解析(附加注释):
public int orangesRotting(int[][] grid){
//Entry存放位置
Queue q=new LinkedList<>();
int row=grid.length;
int col=grid[0].length;
//已经腐烂的位置入队
for(int i=0;i=row||nx<0||ny>=col|ny<0||grid[nx][ny]!=1){
continue;
}
//标记有新的被腐烂的橘子
flag=1;
//如果前面的判定跳过了 说明当前橘子可以被腐烂
grid[nx][ny]=2;
//已经成为腐烂的橘子就放入队列
q.offer(new pair(nx,ny));
}
}
//如果有新的腐烂
if(flag==1){
step++;
}
}
//判断 是否 还有无法腐烂的
for(int i=0;i 2.3、单词接龙
使用方法:广度优先搜索
题目源于力扣:力扣
(1) 通过广度优先搜索,首先将beginWord带出转换一个字母之后所有可能的结果
(2)每一步都要把队列中上一步添加的所有单词转换一遍,最短的转化肯定在这些单词中,所有这些单词的转换只能算一次转换,其实每次队列每次也只针对一个单词,单词的每个字符都会被26个字母换一遍直到对应词典找到了
(3)把转换成功的新词入队,进行下一步的转换
(4)最后整个转换的长度和广度优先搜索次数一致
代码解析(附加注释):
public int ladderLength(String beginword , String endWord, List wordList){
//hash表的查询效率最高
Set wordDict=new HashSet<>();
for(String wd: wordList){
wordDict.add(wd);
}
//标记单词是否已经访问过, 访问过的不再访问
Set visited=new HashSet<>();
visited.add(beginword);
//初始化队列
Queue q=new LinkedList<>();
//将首个单词 放入队列进行广度优先
q.offer(beginword);
int res=1;
while(!q.isEmpty()){
int nextSize=q.size();
//每一步都要把队列中上一步添加的所有单词转换一遍
//最短的转换肯定在这些单词当中,所有这些词的转换只能算一次转换
//因为都是上一步转换出来的
while(nextSize--!=0){
//顶部位置
String curword=q.peek();
q.poll();
//尝试转换当前单词的每一个位置
for(int i=0;i 2.4、打开转盘锁
使用方法:广度优先搜索
题目源于力扣:力扣
题目描述:
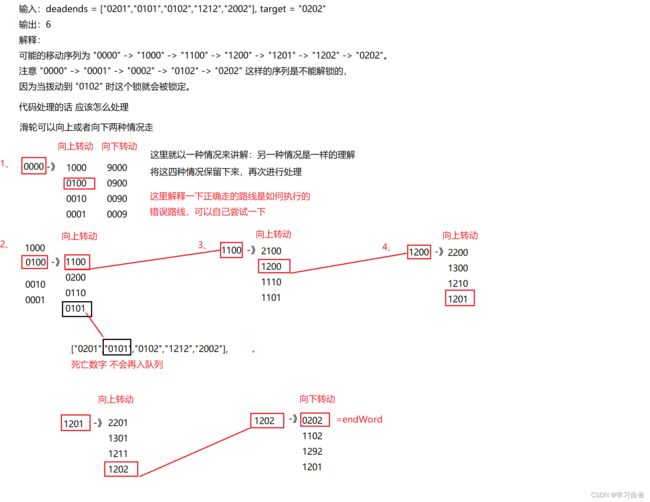
(1)锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
(2)列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
(3)字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
代码解析(附加注释):
public int openLock(String[] deadends,String target){
Set deadendsSet=new HashSet<>();
//将死亡数字进行存储,去重 后面进行判断拨动的转轮数字是不是被包含在这些死亡数字中
for(String str :deadends){
deadendsSet.add(str);
}
//如果“0000” 在死亡数字中,则永远开不了 直接结束
if(deadendsSet.contains("0000")){
return -1;
}
//初始化队列
Queue que=new LinkedList<>();
//添加当前初识值
que.offer("0000");
//创建一个标记位,已经播过的数字不在进行重复出现
Set book=new HashSet<>();
book.add("0000");
//需要拨动几次
int step=0;
while(!que.isEmpty()){
int n= que.size();
//从上一步转换之后的字符串都需要进行验证和转换
//并且只算做一次转换, 类似于层序遍历,转换的步数和层相同
//同一层的袁术都是经过一步转换得到的
for(int i=0;i