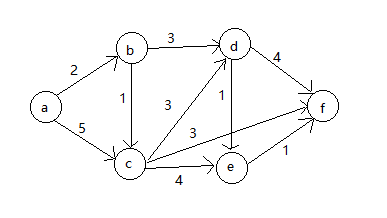
图最短路径算法
图最短路径算法
-
- 迪杰斯特拉算法
- 弗洛伊德算法
- BFS
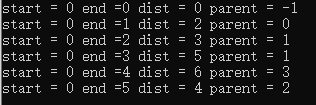
迪杰斯特拉算法
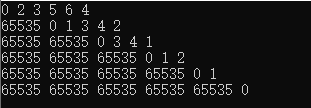
#include弗洛伊德算法
求所有点之间的最短路径
#includeBFS
广度优先遍历求两个点之间的最短路径
当遍历到目标节点,停止遍历,BFS求的是start到end之间的直线距离
1 -5
/ \ \
0 3-4
\ 2 /
求0,4的最短路径
#include