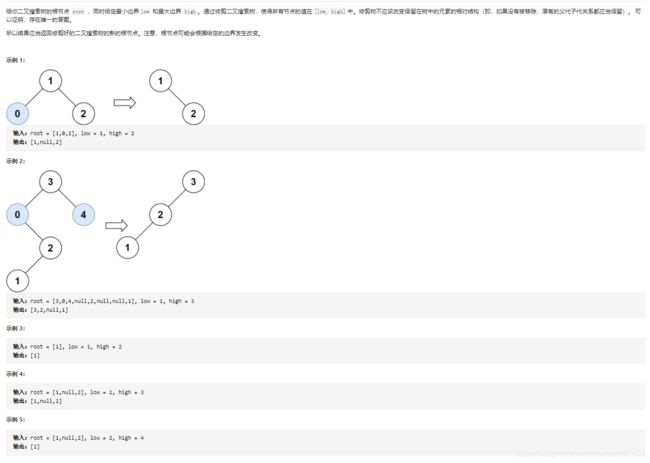
LeetCode刷题笔记——递归问题

一、递归的基本概念

1.1、什么是递归

所谓递归，就是程序调用自身的编程技巧。递归的方法或函数一定是有参的，但在对参数本身进行操作的情况下可以无返回值

1.2、递归类题目的特点

从递归的概念可以看出，递归类问题的最重要的特点就是一个大问题总能拆分成结构类似的小问题，最常见的像快速排序算法的实现，一个大组根据分界值可以分成左右两个小组，两个小组又可以分别各自的分界值进行分类，根据这一“”大问题分成类似小问题“的判断方式，就可以很容易地判断出哪些题目该通过递归的方式解决，下面就给出各个递归题目的详解。

二、递归题目详解

2.1、快速排序算法

 public void quickSort(int[] arr, int left, int right) {

        //递归的出口条件，这在递归当中是必须的
        if (left > right) {
            return;
        }

        int i = left, j = right;
        
        while(i != j){
            //找出第一个不比分界值小的位置
            while(arr[i] < arr[left] && i < j){
                i++;
            }
            //找出第一个不比分界值大的位置
            while(arr[j] > arr[left] && i < j ){
                j--;
            }
            //交换这两个位置
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
        //基准值归位
        int temp = arr[left];
        arr[left] = arr[i];
        arr[i] = temp;

        //左侧数组快速排序，此处为递归
        quickSort(arr,left,i - 1);
        //右侧数组快速排序，此处为递归
        quickSort(arr,i + 1,right);
    }

可以看出，递归代码的最主要特点就是对自身的调用，而要保证程序不会进入死循环，也必须要设置递归的出口。

2.2、合并两个有序链表

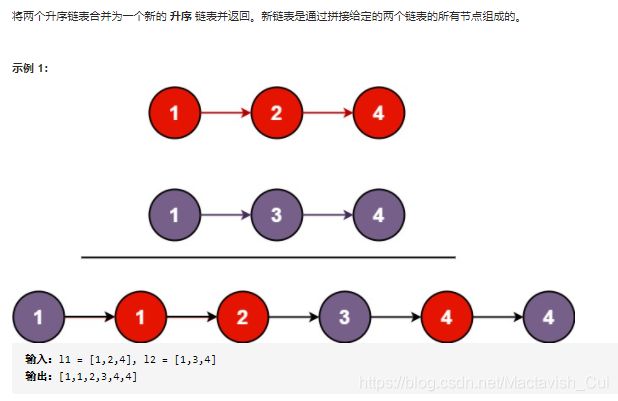
这就是一个典型的递归问题，我们假设第一个链表的头部值更小，那么合并这两个链表的问题就可以拆分成去掉头部值后的第一个列表与第二个列表的合并问题，这是典型的”大问题拆分成结构类似的小问题“，所以采取以下的解题思路

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        //递归出口
        if(l1 == null){
            return l2;
        } else if (l2 == null) {
            return l1;
            //注意能用else if全部连接起来的块不要用独立的if，这道题如果采用了独立的if会增加1ms的运行时间
        //取处子问题进行递归
        } else if(l1.val < l2.val){
            l1.next = mergeTwoLists(l1.next,l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1,l2.next);
            return l2;
        }
    }
}

2.3、二叉树最大深度问题

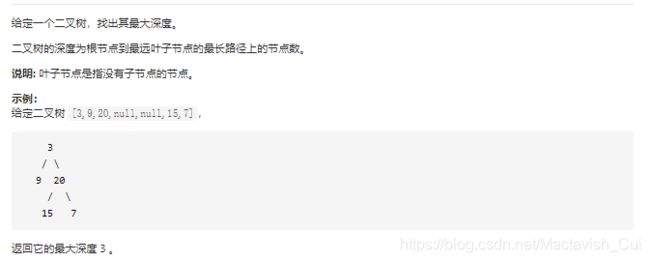
一个二叉树的根节点拥有左右两个子节点，因此最大的树深度就是1（根节点本身拥有一个深度）加上左子树和右子树的深度的最大值，所以问题又会拆分成寻找左子树和右子树的最大深度，是一个与“大问题”相类似的小问题，要用到递归。
递归的过程明确了，那么下一个问题就是递归的出口在哪里，显然，当一个树节点为空的时候，该处及其子节点便不再贡献深度，因此出口便是节点为空的情况，下面给出具体的代码解。

    /**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
    public int maxDepth(TreeNode root) {
        //递归出口：如果节点为空，那么递归结束
        if (root == null) {
            return 0;
        } else {
            //递归的过程，节点不为空的情况下，本节点贡献一个深度，再加上子树的最大深度，就可以得到整个二叉树的最大深度
            return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
        }
    }

2.4、平衡二叉树判断

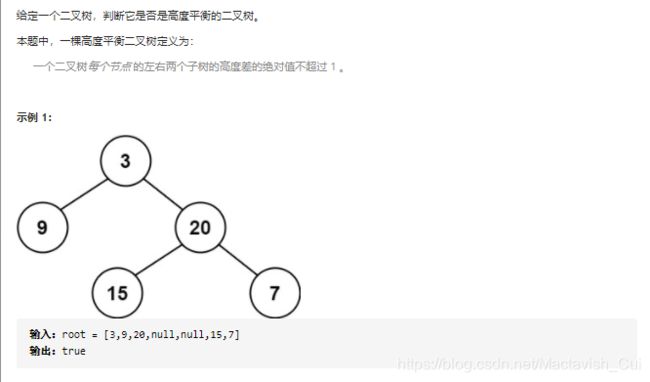
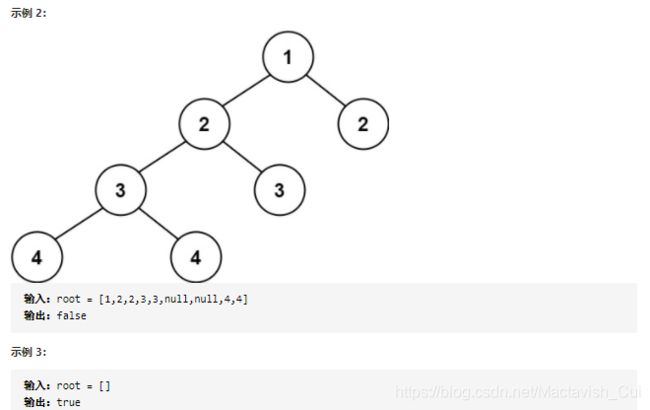
题目的描述中有一个关键点是值得注意的，就是平衡二叉树的每一个节点的左右子树的高度差不超过一，关键词是“每一个节点”，所以就可以把整棵树的判断问题拆分成对每一个节点的拆分的判断，这又符合递归问题的“大问题拆分成相似的小问题”的原则了。下面就给出具体的代码实现。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        //空树或叶节点本身肯定是平衡的，因此搜索到最底之后返回true，这里是递归的出口
        if (root == null){
            return true;
        //某一根节点是平衡的有两个条件
        //第一是左右子树的高度差不超过一，这里注意要使用绝对值，第一次做的时候没用绝对值，所以出错了
        } else if (Math.abs(getDeepth(root.left) - getDeepth(root.right)) > 1){
            return false;
        } else {
        //第二就是要求左右子树都是平衡的，因此取与操作，进行返回
            return isBalanced(root.left) && isBalanced(root.right);
        }
    }

	//寻找树高度的方法，这是跟二叉树最大深度问题一致的
     public int getDeepth(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return 1 + Math.max(getDeepth(root.left), getDeepth(root.right));
        }
    }
}

2.5、二叉树的坡度

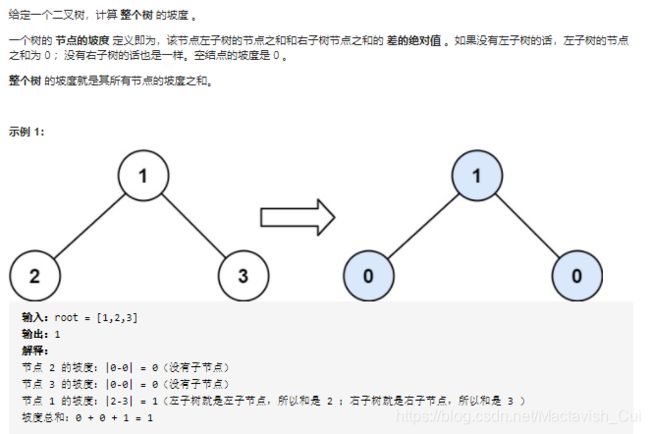
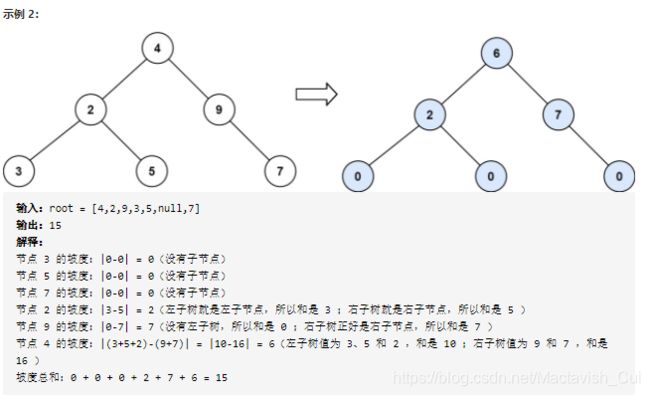
从题目描述可以看出，二叉树的坡度就等于各个子节点的坡度，因此这个问题就又成为了“结构相似的小问题”，而每个节点的坡度又等于左右子树的节点值的和的绝对值差，因此，可以很容易地得到如下的双递归解法

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Solution {
    //双递归解决方案，但是效率太低
    public int findTilt(TreeNode root) {
    	//递归的出口
        if (root == null){
            return 0;
        } else {
        	//左右子树的坡度加本身的坡度
            return findTilt(root.left) + findTilt(root.right) + Math.abs(getSum(root.left) - getSum(root.right));
        }
    }

    public int getSum(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return root.val + getSum(root.left) + getSum(root.right);
        }
    }
}

但是这种方法存在极大的效率低下的问题，可以看到，求和与求坡度节点递归了两次。我们不妨找一种方法来将两次递归的任务合并在一次递归当中。即递归的时候既求出节点值的和，又记录坡度的和，下面给出代码的具体实现

//此处定义的是各个子节点的坡度之和，全局变量
    int sum = 0;

    public int findTilt2(TreeNode root) {
        //调用求和方法，此时的sum已经记录了节点和，因此只返回sum即可
        getSum2(root);
        return sum;
    }
    
    //主体是一个求节点和的方法，但是其中捎带着记录了坡度的和
    public int getSum2(TreeNode root) {
        //递归的出口，空节点不贡献值
        if (root == null) {
            return 0;
        } else {
            //递归得出左右节点之和
            int leftSum = getSum2(root.left);
            int rightSum = getSum2(root.right);
            //左右节点的和的差就是当前节点的坡度
            sum += Math.abs(leftSum - rightSum);
            //这是为了递归，返回当前节点的值的和
            return leftSum + rightSum + root.val;
        }
    }

2.6、二叉树搜索节点最小距离

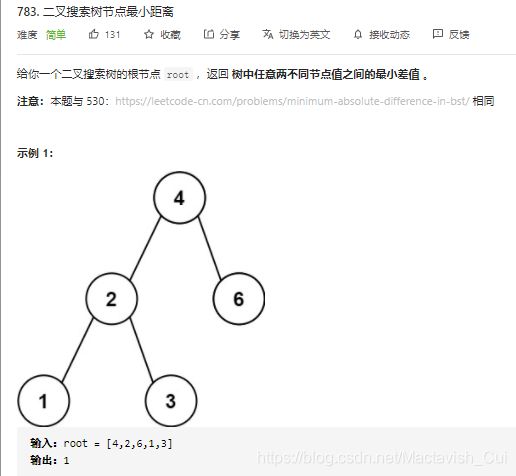
首先需要明确的是，二叉搜索树的特点在于任意一个树节点左子树的值都小于其本身的节点值，右节点的值都大于其本身的节点值，而对二叉搜索树进行中序遍历是能够得到一个有序的数组的，而有序数组的两数最小差值一定在两个相邻的数之间，这样就比较容易得出题解如下了

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
 //注意 这一二叉搜索树的节点值都是大于0的
class Solution {
	//用于记录上一个节点的值，如果未曾经历过节点，则为1
    int pre = -1;
    //用于记录最小的差值
    int diff = Integer.MAX_VALUE;

    public int minDiffInBST(TreeNode root) {
        inorder(root);
        return diff;
    }

    public void inorder(TreeNode root){
    	//遍历到叶子节点后即到达递归终点
        if (root == null) {
            return;
        }
        //遍历左子树
        inorder(root.left);
        //如果第一次遍历到值，将pre置成当前节点值
        if (pre == -1) {
            pre = root.val;
        } else {
        	//并非第一次遍历到，那就求出该值与前一值的差，选最小
            diff = Math.min(diff,root.val - pre);
            //该节点操作结束。将pre设置为当前的值，为后面的工作做准备
            pre = root.val;
        }
        //遍历右子树
        inorder(root.right);
    }
}

可以看到这一题跟二叉树坡度问题都是采用递归进行遍历，遍历过程中做相应操作的题目，都采用了全局变量的设置。

2.7、递增顺序查找树

采用了构造新树的方法，但是注意不要把节点直接拿来赋值，会出现左右子树污染的情况

public class Solution {
    boolean flag = true;
    TreeNode newRoot;
    TreeNode tempRoot;

    public TreeNode increasingBST(TreeNode root) {
        inorder(root);
        return newRoot;
    }

    public void inorder(TreeNode root){
        if (root == null) {
            return;
        }
        inorder(root.left);

        if (flag) {
            flag = false;
            //这里之所以新new一个节点而不是直接tempRoot = root是因为root本身是有左右子节点的，因此会出现树有循环的问题
            tempRoot = newRoot = new TreeNode(root.val);
        } else {
            tempRoot.right = new TreeNode(root.val);
            tempRoot = tempRoot.right;
        }

        inorder(root.right);
    }

2.8、两数相加

blic class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        return addTwoNumbers1(l1, l2, 0);
    }

    public ListNode addTwoNumbers1(ListNode l1, ListNode l2, int number) {
        //递归出口，l1、l2为null且无进位的时候，返回空节点
        if (l1 == null && l2 == null & number == 0)
            return null;
        //这个是为了防止出现空指针异常，如果是空，就认为是值为0的节点
        int l1val = l1 == null ? 0: l1.val;
        int l2val = l2 == null ? 0: l2.val;

        //为了进位与设置当前节点的值
        int sum = l1val + l2val + number;
        //结果挂载一个新节点
        ListNode listNode = new ListNode(sum % 10);
        //递归，同样采用了三元表达式防止出现空指针异常，null.next是无意义的，因此，如果是null，其下一个节点也是null，直接赋值null就好了
        listNode.next = addTwoNumbers1(l1 == null ? null : l1.next, l2 == null ? null : l2.next, sum / 10);
        return listNode;
    }

2.9、电话号码的数字组合

这里需要注意的是，数字不仅有2个的组合，还有三个乃至更多的数字之间的组合。假设数字23的组合得到 了六组字符串，那么数字234的组合就是数字4所对应的三个字母与23组合得到的六个字符串的组合，那么要得到234的字母组合，就是在23的字母组合的基础上与4对应的字母组合，就成为了结构相似的大问题与小问题，自然就会联想到递归的解法，下面给出代码

public List<String> letterCombinations(String digits) {
        return Arrays.asList(getCombination(digits));
    }

    public String[] getCombination(String digits){
        Map<Character,String[]> map = new HashMap<>();
        map.put('2',new String[]{"a", "b", "c"});
        map.put('3',new String[]{"d", "e", "f"});
        map.put('4',new String[]{"g", "h", "i"});
        map.put('5',new String[]{"j", "k", "l"});
        map.put('6',new String[]{"m", "n", "o"});
        map.put('7',new String[]{"p", "q", "r", "s"});
        map.put('8',new String[]{"t", "u", "v"});
        map.put('9',new String[]{"w", "x", "y", "z"});

        int length = digits.length();
        //字符串为0直接返回空字符串
        if (length == 0) {
            return new String[]{};
        } 
        //字符串为1直接返回其对应的字符串
        else if (length == 1) {
            return map.get(digits.charAt(0));
        }
        //两个以上的数字的情况 
        else {
        	//获取除去第一个数字之外的其他数字的组合
            String[] combination = getCombination(digits.substring(1));
            //定义存储结果的数组
            int length1 = combination.length;
            int length2 = map.get(digits.charAt(0)).length;
            String[] result = new String[length1 * length2];
            int index = 0;
            //将第一个数字的字母与得到的组合数组进行组合
            for (String s : map.get(digits.charAt(0))) {
                for (String s1 : combination) {
                    result[index] = s + s1;
                    index ++;
                }
            }
            //返回结果数组
            return result;
        }
    }

这段代码有两个需要注意之处，第一是数字与字母的对应关系采用了哈希表的方式存储，因为这样查询的速率是很快的。第二是之所以用了字符串数组转List返回的方式而不是对List直接进行递归，是因为List的递归会产生ConcurrentModificationException异常，涉及到了对象的并发修改

2.10、两两交换列表中的节点

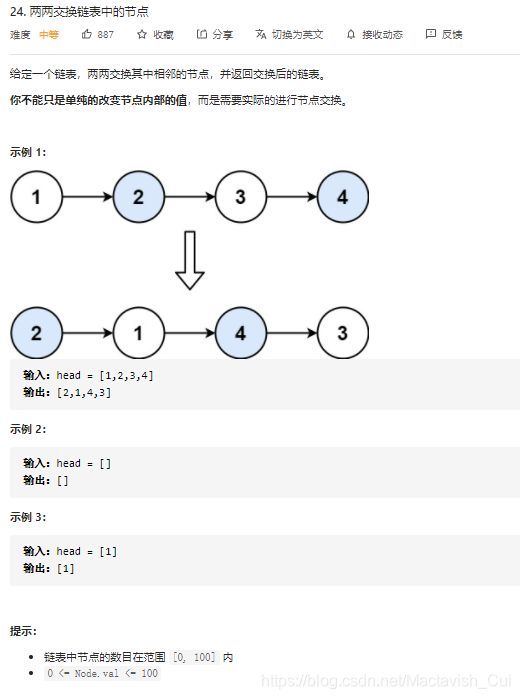
最终得到的链表等于前两个节点交换，然后与一个两两交换后的链表的连接，因此就成了一个递归问题

public class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head == null){
            return null;
        } else if (head.next == null) {
            return head;
        } else {
            ListNode temp_1 = new ListNode(0);
            ListNode temp_2 = new ListNode(0);
            //临时记录第一节点第二节点
            temp_1.next = head;
            temp_2.next = head.next;

            //原一节点指向三节点
            temp_1.next.next = temp_2.next.next;
            //原二节点指向一节点
            temp_2.next.next = temp_1.next;

            //更改之后头部节点变成了原二节点，也就是temp_2.next
            //连接新节点与递归后的节点
            temp_1.next.next = swapPairs(temp_1.next.next);
            return temp_2.next;
        }
    }
}

2.11、验证二叉搜索树

这里再次应用了二叉搜索树中序遍历的性质：即二叉搜索树中序遍历得到的是一个有序数组，因此只需要进行中序遍历然后判断是否是有序数组即可，这里采用的方法是记录前一个值，将其与后一个值比较，如果不符合有序，则将全局的result置为false，最后返回false即可

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    boolean result = true;
    int pre = -1;
    
    public boolean isValidBST(TreeNode root) {
        getAllNodes(root);
        return result;
    }
    
    public void getAllNodes(TreeNode root) {
        if (root == null) {
            return;
        } else {
            //中序遍历先遍历左子树
            getAllNodes(root.left);
            
            //如果是第一个节点，不需要判断，只赋值即可
            if (pre == -1) {
                pre = root.val;
            } else {
            	//否则记录result为false，其实记录了false之后就不影响最后的结果了,因此不必再进行多余的赋值操作
                if (root.val <= pre) {
                    result = false;
                    return;
                } else {
                    pre = root.val;
                }
            }
            
            //最后遍历右子树
            getAllNodes(root.right);
        }
    }
}

在这里pre初始值设置得有问题，应该另设置一标志位进行pre是否改变的判断的，因为这里并没有说这个二叉搜索树是任意整型值的，当然也可以设置成DOUBLE的MIN_VALUE来破

2.12、二叉树的右视图

要做这道题肯定是要对二叉树进行遍历的，无非是深度优先和广度优先两种方式，之前递归一直使用的是深度优先的方式，其中一条重要的性质是二叉搜索树采用左节点-根节点-右节点的顺序会得到有序数组，这里又有一个性质就是对二叉树进行根节点-右子树-左子树的顺序，就能保证按照层次，首先遍历到每一层的最右侧的节点，因此可以得到题解如下

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //存储结果
    private List<Integer> result = new ArrayList<>();

    public List<Integer> rightSideView(TreeNode root) {
        dfs(root,0);
        return result;
    }

    //深度优先搜索
    private void dfs(TreeNode root, int deepth) {
        if (root == null) {
            return;
        }
        
        //如果该层对应的索引处没有值，即层深度等于数组长度，则证明该层没有被访问过，可以进行值的存储
        if (deepth == result.size()) {
            result.add(root.val);
        }
        deepth ++;
        //否则就去访问下一层
        dfs(root.right,deepth);
        dfs(root.left,deepth);
    }
}

除了深度优先遍历之外还有一种做法就是广度优先遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        //记录结果用的数组
        List<Integer> result = new ArrayList<>();
        //空节点特例，提前处理
        if (root == null) {
            return result;
        }
        //队列初始化
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        //广度优先遍历
        while (!que.isEmpty()) {
            //size不止代表了队列的大小，还代表了当前层的节点数
            int size = que.size();
            for (int i = 0; i < size; i++) {
                root = que.poll();
                //先存左，后存右
                if (root.left != null) {
                    que.offer(root.left);
                }
                if (root.right != null) {
                    que.offer(root.right);
                }
                if(i == size - 1) {
                    //存取每一层的最后一个元素
                    result.add(root.val);
                }
            }
        }
        return result;
    }
}

2.13、至少有 K 个重复字符的最长子串

这道题用到了一个非常重要的思想就是“分治”，分治就是通过一定的方法将大的问题拆分成诸多小问题再对小问题进行解决，这与递归的思想是一致的，而分治的核心就在于找出分界点在哪里。
针对这道题来讲，可以看到，如果一个字符出现的次数小于k，那么这个字符一定不会出现在题目所要求的子串当中，因此就可以用这个字符对整个的字符串进行分割。当遇到正确结果不容易找出的时候就可以反着思考是不是要利用错误的结果将正确答案分离开来。下面给出代码的具体实现，

public class Solution {

    /*如果所有的字符都大于k，那么返回true，
    反之如果某一个字符的出现次数少于k，那么该字符一定不会出现在结果字符串当中
    因此只需要采用分治的方法对这个字符串对数组进行分割即可，另外s仅由小写英文字母组成，这点也可以利用，即构建一个长度为26的数组，当然用哈希表的方式进行统计也是可以的*/
    public int longestSubstring(String s, int k) {
        //存储26个字母的数组，索引0对应‘a’，1对应‘b’，以此类推
        int[] count = new int[26];

        //字符串转char数组
        char[] chars = s.toCharArray();
        for(char ch : chars) {
            //计数加一
            count[ch-'a'] ++;
        }

        String split = "";
        for(int i = 0; i < 26; i++) {
            if (count[i] > 0 && count[i] < k) {
                //记录分治标记
                split = Character.toString('a' + i);
            }
        }

        //如果分隔符为空，则整个字符串都是符合要求的，返回字符串的长度即可
        if(split == "") {
            return s.length();
        }

        //否则的话分割得到字符串数组
        String[] strings = s.split(split);

        int result = 0;
        //取分割后的字符串中的最大值
        for (String str : strings) {
            result = Math.max(result,longestSubstring(str,k));
        }

        return result;
    }
 }

2.14、修剪二叉树

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        //处理空节点的特殊情况，同时也是递归的出口，防止爆栈
        if (root == null) {
            return null;
        }
        //非空节点的情况

        //根节点本身就需要被修剪的情况
        //根节点在最小边界外
        if (root.val < low) {
            //舍弃根节点及其左子树，只返回修剪右子树的结果
            return trimBST(root.right,low,high);
        }
        //根节点在最大边界外
        if (root.val > high) {
            //舍弃根节点及其右子树，只返回修剪左子树的结果
            return trimBST(root.left,low,high);
        }
        //根节点不需要修剪的情况，左右分别等于左右子树修剪后的结果
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);

        return root;
    }
}

对于void类型的递归，就是指执行某一个操作，而有返回类型的递归得到的就是执行什么操作后的结果了，这一点要理清，void类型的递归需要对全局变量进行操作。
另外，递归只处理当前的小问题，其他的部分留给另外的递归调用去做吧，不要越俎代庖

2.15、最长同值路径

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {

    //用于存储最大值的全局变量
    int result = 0;

    //返回路径结果
    public int longestUnivaluePath(TreeNode root) {
        dfs(root);
        return result;
    }

    //获得单左侧/单右侧的最大值
    private int dfs(TreeNode root) {
        //空节点或单节点的极端情况
        if (root == null) {
            return 0;
        }
        //左右节点各自的左右最长路径
        int leftLength = dfs(root.left);
        int rightLength = dfs(root.right);

        //用于存储当前节点的左右路径
        int thisLeftLength = 0;
        int thisRightLength = 0;

        //从根节点向左出发
        if (root.left != null && root.left.val == root.val) {
            thisLeftLength = leftLength + 1;
        }
        
        //从根节点向右出发
        if (root.right != null && root.right.val == root.val) {
            thisRightLength = rightLength + 1;
        }

        //因为递归实现了遍历，因此每一个节点的路径值都会在递归的过程中得到，就可以顺便把最大值比较了
        result = Math.max(result,thisLeftLength + thisRightLength);

        //返回左右节点的最大值
        return Math.max(thisLeftLength,thisRightLength);
    }
}

2.16、划分为k个相等子集

class Solution {
	public boolean canPartitionKSubsets(int[] nums, int k) {
        if (k == 1) return true;
        //数组求和
        int sum = 0;
        for(int num : nums) {
        sum += num;
        }
        //分组目标值为非整数的情况
        if (sum % k != 0) {
        return false;
        }

        //每组的目标值，数组最大值的索引，排序后的数组
        int target = sum / k;
        int row = nums.length - 1;
        Arrays.sort(nums);

        if (nums[row] > target) return false;

        //本身等于目标值的数不需要参与排序，因此索引与组数减一
        while (row >= 0 && nums[row] == target) {
            row --;
            k --;
        }

        if (k < 0) return true;

        //至此得到的是数组总和大于分组数乘以目标值的数组
        return search(new int[k],row,nums,target);
        }

	//判断每个数字能否放进子集的方法
	//因为数组总和是大于子集数x目标值的，因此只有两种情况，刚好放进去和有至少一个子集大于目标值
	private boolean search(int[] groups, int row, int[] nums, int target){
        //没有再需要分组的数了就返回true，这里也是递归的出口
        if (row < 0) return true;
        int num = nums[row];
        row--;
        for(int i=0; i < groups.length; i++) {
        if (groups[i] + num <= target) {
        groups[i] += num;
        if (search(groups,row,nums,target)) return true;
        groups[i] -= num;
        }
        //避免重复性工作
        if (groups[i] == 0) break;
        }
        return false;
        }
}