【《WebGL编程指南》读书笔记-绘制和变换三角形】
时隔三天,我的数据结构知识集又加厚了一点,我也该回到WebGL的学习了。
我决定看这本书,一方面的原因是从理解cesium入手,另一方面就是因为这一章。
我在看书之前对书的各个章节大概看了一眼,这一章一开始关于三角形的叙述很吸引人,似乎是三维模型的基础。总目录链接:https://blog.csdn.net/floating_heart/article/details/124001572
第三章 绘制和变换三角形
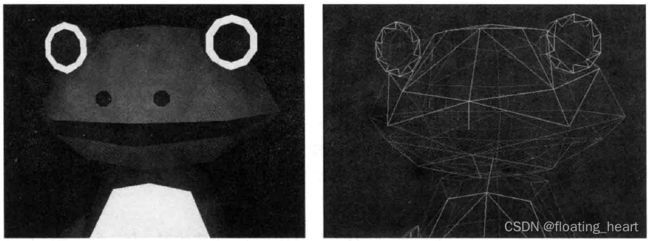
构成三维模型的基本单位是三角形。例如下图左图中的青蛙,就是由右图所示的许多个三角形以及这些三角形的顶点构成的。不管三维模型的形状多么复杂,其基本组成部分都是三角形,只不过复杂的模型由更多的三角形构成而已。通过创建更细小和更大量的三角形,就可以创建更复杂和更逼真的三维模型。比如,游戏角色这种复杂的模型都包含上万个三角形和顶点。因此,如何绘制三角形对渲染三维模型至关重要。
章节开始之前,将本章涉及的内容罗列如下:
- 三角形在三维图形学中的重要地位,以及WebGL如何绘制三角形。
- 使用多个三角形绘制其它类型的基本图形。
- 利用简单的方程对三角形做基本的变换,如移动、旋转和缩放。
- 利用矩阵简化变换。
绘制多个点与缓冲区对象
相关内容:缓冲区对象:创建缓冲区对象-绑定缓冲区对象-向缓冲区对象写入数据以及类型化数组-缓冲区对象分配给attribute变量-开启attribute变量;开始绘制及着色器运行过程
相关函数:gl.createBuffer(), gl.bindBuffer(), gl.bufferData(), new Float32Array()…, gl.vertexAttribPointer()(有自动补全), gl.enableVertexAttribArray(), gl.disableVertexAttribArray(), gl.drawArrays()小结:本节介绍了缓冲区的使用方法,重点在于:1. 缓冲区使用流程;2. 相关WebGL系统结构(保证缓冲区在原结构下的安然运行(符合WebGL系统风格));3. JavaScript类型化数组及其在WebGL系统中的应用;4. 三维基础-三角形及批量输入顶点
之前的示例都是逐个点进行绘制,本节将讨论一次性绘制多个点的方法,作为绘制多顶点图形的基础。本节示例程序名称为MultiPoint,它将接用WebGL缓冲区对象(buffer object),在屏幕上绘制三个红色小点。

缓冲区对象是WebGL系统中的一块内存区域,我们可以一次性地向缓冲区对象中填充大量的顶点数据,然后将这些数据保存在其中,供顶点着色器使用。
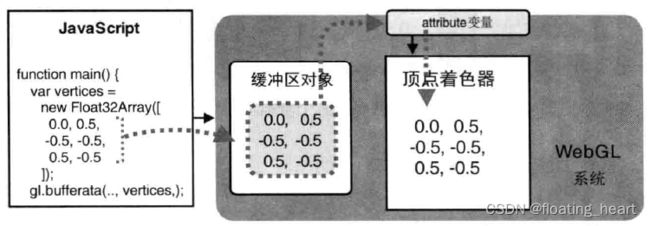
示例程序在传统的流程之外,增加了新的步骤:设置点的坐标信息。完整的流程如下图所示:
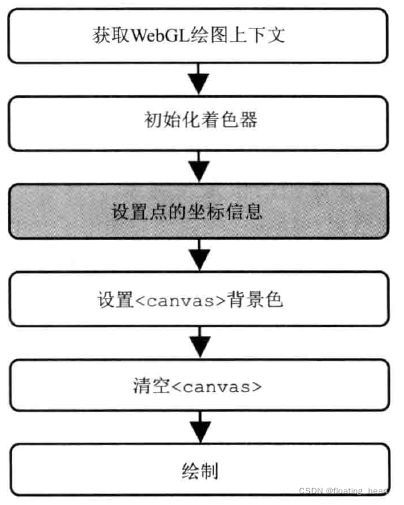
示例程序的代码如下:
// MultiPoint.js
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'void main(){\n' +
' gl_Position = a_Position;\n' +
' gl_PointSize = 10.0;\n' +
'}\n'
// 片元着色器
var FSHADER_SOURCE =
'void main() {\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 主函数
function main() {
// 获取canvas元素
let canvas = document.getElementById('webgl')
// 获取WebGL上下文
let gl = getWebGLContext(canvas)
if (!gl) {
console.log('Failed to get the rendering context for WebGL')
return
}
// 初始化着色器
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to initialize shaders')
return
}
// 设置顶点位置
let n = initVertexBuffers(gl)
if (n < 0) {
console.log('Failed to set the positions of the vertices')
return
}
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空canvas
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制
gl.drawArrays(gl.POINTS, 0, n)
}
function initVertexBuffers(gl) {
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
let n = 3 // 点的个数
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
// 将缓冲区对象绑定到目标
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
// 向缓冲区对象中写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
// 将缓冲区对象分配给a_Position变量
let a_Position = gl.getAttribLocation(gl.program, 'a_Position')
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position')
return -1
}
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
// 连接a_Position变量与分配给它的缓冲区对象
gl.enableVertexAttribArray(a_Position)
return n
}
新加入的函数initVertexBuffers()创建了顶点缓冲器对象,将多个顶点的数据保存在缓冲区中,最后将缓冲区传给顶点着色器。函数的返回值是待绘制顶点的数量,发生错误会返回-1.
示例程序仅调用一次gl.drawArray()函数就完成了绘图操作,函数中显式地说明要绘制多少个点(新函数的返回值)。
我们主要从新函数入手,了解WebGL缓冲区对象的使用方法。
使用缓冲区对象:
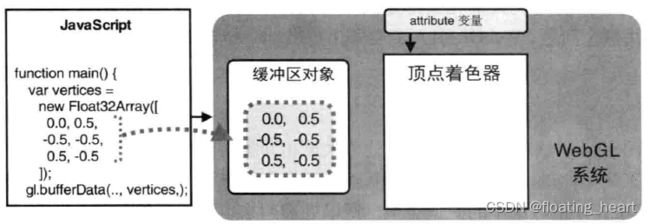
缓冲区对象是WebGL系统中的一块存储区,我们可以在缓冲区对象中保存想要绘制的所有顶点的数据。如下图所示:
在示例程序中,向缓冲区对象写入的顶点坐标是一种特殊的JavaScript数组(Float32Array),稍后会进行介绍:
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
使用缓冲区对象向顶点着色器传入多个顶点的数据,需要遵循以下步骤:
- 创建缓冲区对象(
gl.createBuffer()) - 绑定缓冲区对象(
gl.bindBuffer()) - 将数据写入缓冲区对象(
gl.bufferData()) - 将缓冲区对象分配给一个attribute变量(
gl.vertexAttribPointer()) - 开启attribute变量(
gl.enableVertexAttribArray())
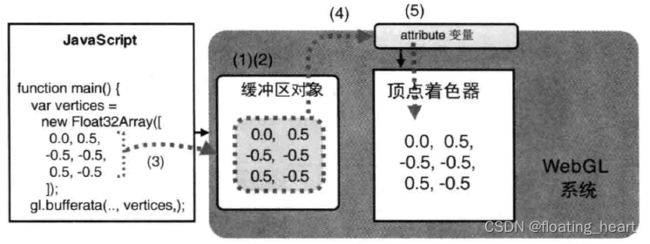
下面分别进行解析。
创建缓冲区对象(gl.createBuffer()):
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
创建缓冲区对象采用gl.createBuffer()函数,函数规范如下:
gl.createBuffer():创建缓冲区对象。
**参数:**无
返回值:
非null:新创建的缓冲区对象
null:创建缓冲区对象失败
**错误:**无
相应的,gl.deleteBuffer(buffer)函数可以删除被上一个函数创建出的缓冲区对象,其函数规范如下:
gl.deleteBuffer(buffer):创建缓冲区对象。
参数:
buffer:待删除的缓冲区对象
返回值: 无
错误: 无
创建缓冲区前后WebGL系统的变化如下图所示:执行后WebGL系统中多出了“缓冲区对象”

绑定缓冲区对象(gl.bindBuffer()):
// 将缓冲区对象绑定到目标
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
创建缓冲区对象后,需要将其绑定到WebGL系统中已经存在的“目标”(target)上。“目标”表示缓冲区对象的用途(示例中为向顶点着色器提供传给attribute变量的数据),这样WebGL才能够正确处理其中内容。
绑定缓冲区对象采用的函数为gl.bindBuffer(),函数规范如下:
gl.bindBuffer(target, buffer):允许使用buffer表示的缓冲区对象并将其绑定到target表示的目标上。
参数:
target参数可以是以下中的一个:
gl.ARRAY_BUFFER 表示缓冲区对象中包含了顶点的数据
gl.ELEMENT_ARRAY_BUFFER 表示缓冲区对象中包含了顶点的索引值(参见第6章着色器语言GLSL ES)
buffer:待删除的缓冲区对象
返回值: 无
错误:
INVALID_ENUM target不是上述值之一,这时将保持原有的绑定情况不变
示例程序中,我们将创建的缓冲区对象绑定到gl.ARRAY_BUFFER目标上,代码执行完毕后,WebGL系统内如下图所示:

向缓冲区对象中写入数据(gl.bufferData()):
// 向缓冲区对象中写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
这一步将vertices中的数据写入到绑定在gl.ARRAY_BUFFER目标的缓冲区对象。此处不能直接向缓冲区写入数据,而是依据target写入数据,所以在此之前target下需要有绑定的缓冲区对象。
gl.bufferData()的函数规范如下:
gl.bufferData(target, data, usage):开辟存储空间,向绑定在target上的缓冲区对象中写入数据。
参数:
target:gl.ARRAY_BUFFER 或 gl.ELEMENT_ARRAY_BUFFER
data:写入缓冲区对象的数据(类型化数组)
usage:表示程序将如何使用存储在缓冲区对象中的数据。该参数将帮助WebGL优化操作,但是就算你传入了错误的值,也不会终止程序(仅仅是降低程序的效率)
gl.STATIC_DRAW 只会向缓冲区对象中写入一次数据,但需要绘制很多次(many times)
gl.STREAM_DRAW 只会向缓冲区对象中写入一次数据,然后绘制若干次(at most a few times)
gl.DYNAMIC_DRAW 会向缓冲区对象中多次写入数据,并绘制很多次(many times)
返回值: 无
错误:
INVALID_ENUM target不是上述值之一,这时将保持原有的绑定情况不变
类型化数组:
在gl.bufferData()方法中,data参数需要提供类型化数组。在示例中,我们定义的类型化数组如下所示:
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
Float32Array()提供了32位浮点数数组,通常用来存储顶点的坐标或颜色数据。
WebGL使用的各种类型化数组如下所示:
| 数组类型 | 每个元素所占字节数 | 描述(C语言中的数据类型) |
|---|---|---|
| Int8Array | 1 | 8位整型数(signed char) |
| UInt8Array | 1 | 8位无符号整型数(unsigned char) |
| Int16Array | 2 | 16位整型数(signed short) |
| UInt16Array | 2 | 16位无符号整型数(unsigned short) |
| Int32Array | 4 | 32位整型数(signed int) |
| UInt32Array | 4 | 32位无符号整型数(unsigned int) |
| Float32Array | 4 | 单精度32位浮点数(float) |
| Float64Array | 8 | 双精度64位浮点数(double) |
与JavaScript中的Array类似,类型化数组也有一系列方法和属性,但不支持push()和pop()。详情如下:
| 方法、属性和常量 | 描述 |
|---|---|
| get(index) | 获取第index个元素值 |
| set(index, value) | 设置第index个元素的值为value |
| set(array, offset) | 从第offset个元素开始将数组array中的值填充进去 |
| length | 数组的长度 |
| BYTES_PER_ELEMENT | 数组中每个元素所占的字节数 |
类型化数组的创建方式和一般类的实例的创建方式相同,有两种:
- 第一种使用new运算符传入普通数组:与示例中一致
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
- 第二种使用new运算符指定元素的个数:
let vertices = new Float32Array(4)
JavaScript中通用的数组Array并不强调数组元素的类型一致,也没有对同类型大量元素的处理进行优化。WebGL为每种基本数据类型引入类型化数组,提前告诉浏览器数组中的数据类型,能够更有效率地处理数据,为绘制三维图形提供了大量便利。
将缓冲区对象分配给一个attribute变量(gl.vertexAttribPointer()):
缓冲区对象准备好之后,需要获取attribute变量地址,再向attribute变量传递参数。第二章中使用了gl.vertexAttrib[1234]f[v]系列函数来传递数据,但此方法一次只能传递一个值,此时需要一次传递多个值,示例中采用gl.vertexAttribPointer()方法。
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
该函数的规范如下:
gl.vertexAttribPointer(location, size, type, normalized, stride, offset):
将绑定到gl.ARRAY_BUFFER的缓冲区对象(实际上是其引用或指针)分配给由location指定的attribute变量。
参数:
location:指定待分配attribute变量的存储位置
size:指定缓冲区中每个顶点的分量个数(1到4)。若size比attribute变量需要的分量数小,缺失分量将按照与gl.vertexAttrib[1234]f()相同的规则补全。比如,如果size为1,那么第2、3分量自动设为0,第4分量为1。
type:用以下类型之一来指定数据格式
gl.UNSIGNED_BYTE 无符号字节,Uint8Array
gl.SHORT 短整型,Int16Array
gl.INT 整型,Int32Array
gl.UNSIGNED_INT 无符号整型,UInt32Array
gl.FLOAT 浮点型,Float32Array
normalize:传入true或false,表明是否将非浮点型的数据归一化到[0,1]或[-1,1]区间(正则化)
stride:指定相邻两个顶点间的字节数,默认为0(参见第5章)
offset:指定缓冲区对象中的偏移量(以字节为单位),即attribute变量从缓冲区中的何处开始存储。如果是从起始位置开始的,offset设为0。
返回值: 无
错误:
INVALID_OPERATION 不存在当前程序对象
INVALID_VALUE location大于等于attribute变量的最大数目(默认为8)。或者stride或offset是负值。
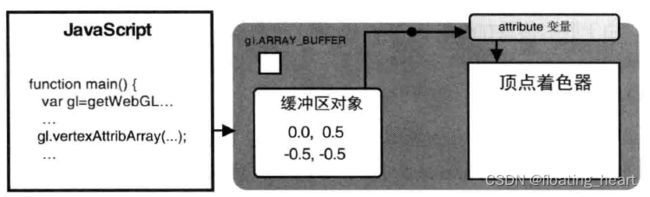
执行完毕后,gl.ARRAY_BUFFER缓冲区对象被分配给attribute变量,此时缓冲区对象还不可用,如下图所示:

开启attribute变量(gl.enableVertexAttribArray()):
虽然前一步已经将attribute变量指向了缓冲区对象,但此时着色器还不能访问缓冲区内的数据,需要使用先开启attribute变量。示例中的代码如下:
// 连接a_Position变量与分配给它的缓冲区对象
gl.enableVertexAttribArray(a_Position)
相关函数的函数规范如下:
gl.enableVertexAttrirbArray(location):
开启location指定的attribute变量(实际处理对象是缓冲区)。
参数:
location:指定attribute变量的存储位置
返回值: 无
错误:
INVALID_VALUE location大于等于attribute变量的最大数目(默认为8)。
开启attribute变量之后,缓冲区对象和attribute变量之间的连接就真正建立起来了,如下图所示:
开启attribute变量之后,我们就不能通过gl.vertexAttrib[1234]f()来向该变量传递数据了,实际上也不应该同时通过两种方式传递数据。
于是,我们也可以通过gl.disableVertexAttribArray()来关闭分配,函数规范如下:
gl.enableVertexAttrirbArray(location):
关闭location指定的attribute变量。
参数:
location:指定attribute变量的存储位置
返回值: 无
错误:
INVALID_VALUE location大于等于attribute变量的最大数目(默认为8)。
开始绘制:
通过上面的函数,我们已经配置好了缓冲区和着色器,可以开始绘制:
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空canvas
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制
gl.drawArrays(gl.POINTS, 0, n)
绘制同样采用gl.drawArrays()方法,该方法函数规范在第二章已经给出,此处给出函数语法作为提示:
gl.drawArrays(mode, first, count)
示例中n=3,count为3,所以顶点着色器实际执行了3次。
在建立attribute变量和缓冲区联系时,函数gl.vertexAttribPointer()中的参数size为2,表示缓冲区每个顶点有2个分量值。所以每次着色器运行前,gl_Position都被提供了两个分量(通过attribute变量a_Position),其他值按照规则填充为0.0和1.0。
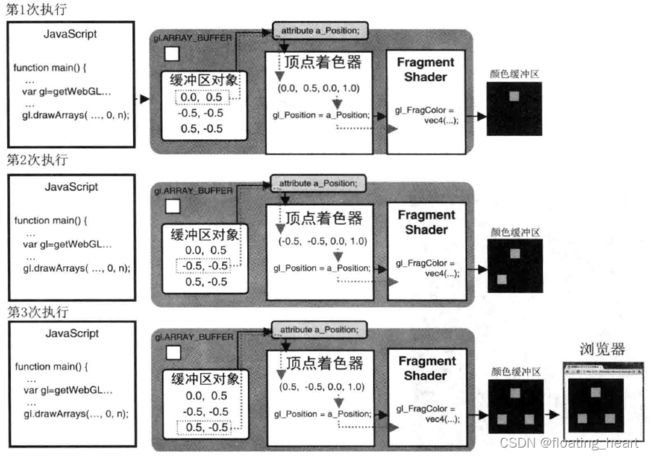
绘制过程如下图所示:
Hello Triangle与gl.drawArrays()更多的基本图形
相关内容:WebGL绘制基本图形
相关函数:gl.drawArrays()mode参数小结:1.WebGL只能绘制点、线段和三角形,通过这些基本图形构成复杂模型;2.顶点顺序对图形绘制有重要影响;3. gl.drawArrays()中的mode参数规定了绘制图形和使用顶点的方式。
通过缓冲器,我们可以将多个坐标传递给顶点着色器,下面我们将运用这些坐标绘制一个简单的三角形,效果如下:
示例程序HelloTriangle.js如下:
// MultiPoint.js
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'void main(){\n' +
' gl_Position = a_Position;\n' +
'}\n'
// 片元着色器
var FSHADER_SOURCE =
'void main() {\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 主函数
function main() {
// 获取canvas元素
let canvas = document.getElementById('webgl')
// 获取WebGL上下文
let gl = getWebGLContext(canvas)
if (!gl) {
console.log('Failed to get the rendering context for WebGL')
return
}
// 初始化着色器
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to initialize shaders')
return
}
// 设置顶点位置
let n = initVertexBuffers(gl)
if (n < 0) {
console.log('Failed to set the positions of the vertices')
return
}
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空canvas
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制
gl.drawArrays(gl.TRIANGLES, 0, n)
}
function initVertexBuffers(gl) {
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
let n = 3 // 点的个数
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
// 将缓冲区对象绑定到目标
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
// 向缓冲区对象中写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW)
// 将缓冲区对象分配给a_Position变量
let a_Position = gl.getAttribLocation(gl.program, 'a_Position')
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position')
return -1
}
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
// 连接a_Position变量与分配给它的缓冲区对象
gl.enableVertexAttribArray(a_Position)
return n
}
相对于上一示例,此处存在两处改动:
- 顶点着色器中删除了
' gl_PointSize = 10.0;\n',该语句只在绘制单个点的时候才起作用; gl.drawArrays()方法第一个参数改为了gl.TRIANGLES(第37行)
gl.drawArrays()就是我们绘制众多基本图形的重要方法,下面进行说明。
基本图形与gl.drawArrays()方法:
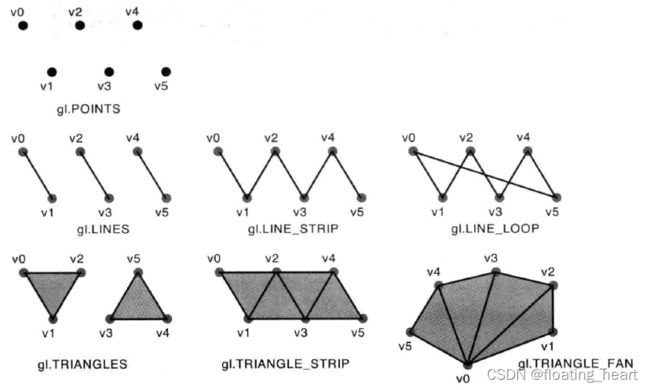
gl.drawArrays()方法强大又灵活,可以通过第1个参数mode指定不同的值来以7种不同的方式绘制图形。WebGL可以绘制的基本图形如下:
| 基本图形 | 参数mode | 描述 |
|---|---|---|
| 点 | gl.POINTS | 一系列点,绘制在v0、v1、v2······处。 |
| 线段 | gl.LINES | 一系列单独的线段,绘制在(v0,v1)、(v2,v3)、(v4,v5)······处,如果点的个数是奇数,最后一个点将被忽略。 |
| 线条 | gl.LINE_STRIP | 一系列连接的线段,将被绘制在(v0,v1)、(v2,v3)、(v4,v5)······处,第1个点是第1条线段的起点,第2个点是第1条线段的终点和第2条线段的起点······第i(i>1)个点是第i-1条线段的终点和第i条线段的起点,以此类推。最后一个点是最后一条线段的终点。 |
| 回路 | gl.LINE_LOOP | 一系列连接的线段。与gl.LINE_STRIP绘制的线条相比,增加了一条从最后一个点到第1个点的线段。因此,线段被绘制在(v0,v1)、(v1,v2)······(vn,v0)处,其中,vn是最后一个点。 |
| 三角形 | gl.TRAINGLES | 一系列单独的三角形,绘制在(v0,v1,v2)、(v3,v4,v5)······处。如果点的个数不是3的整数倍,最后剩下的一或两个点将被忽略。 |
| 三角带 | gl.TRIANGLE_STRIP | 一系列条带状的三角形,前三个点构成了第1个三角形,从第2个点开始的三个点构成了第2个三角形(该三角形与前一个三角形共享一条边),以此类推。这些三角形被绘制在(v0,v1,v2)、(v2,v1,v3)、(v2,v3,v4)······处(第2个三角形是(v2,v1,v3)而不是(v1,v2,v3)是为了保持第2个三角形的绘制也是按照逆时针的顺序)。 |
| 三角扇 | gl.TRIANGLE_FAN | 一系列三角形组成的类似于扇形的图形。前三个点构成了第1个三角形,接下来的一个点和前一个三角形的最后一条边组成接下来的一个三角形。这些三角形被绘制在(v0,v1,v2)、(v0,v2,v3)、(v0,v3,v4)······处。 |
下图展示了这些基本图形:
关于这些基本图形,值得注意的有两点:
- 顶点的顺序对图形的呈现有重要影响;
- WebGL只能绘制三种图形:点、线段和三角形。当然,从球体到立方体,再到游戏中的三维角色,都可以由小的三角形组成,实际上,我们可以使用以上这些最基本的图形来绘制出任何东西。
我们可以在示例程序中修改mode参数,得到不同的呈现结果,此处不再进行展示。
用三角形绘制矩形(HelloQuad)
既然任何东西都可以由基本图形构成,那么我们来绘制一个矩形,体会这种“构成”的方式。
矩形可以由两个三角形组成,绘制方式可以采用gl.TRAINGLES、gl.TRIANGLE_STRIP、gl.TRIANGLE_FAN三种方法,第一种方法需要用到6个顶点,后两种需要4个顶点,每种方法的顶点顺序都不相同。此处采用gl.TRIANGLE_STRIP方法进行绘制,相比于上个示例,此处改动如下:
- 顶点坐标位置改动
let vertices = new Float32Array([-0.5, 0.5, -0.5, -0.5, 0.5, 0.5, 0.5, -0.5]) # 正方形的四个顶点,点的顺序可见上一节gl.TRIANGLE_STRIP图形示例
- 点的个数n从3改为4
let n = 4 // 点的个数
- gl.drawArrays()的mode参数改为gl.TRIANGLE_STRIP
// 绘制
gl.drawArrays(gl.TRIANGLE_STRIP, 0, n)
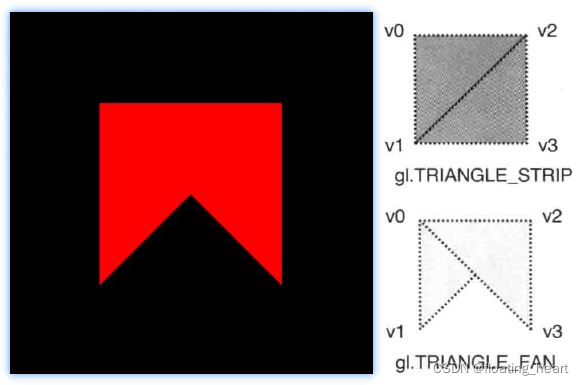
绘制的结果如下:
顶点顺序的尝试:
此处如果把HelloQuad中gl.drawArrays()的mode参数改为gl.TRIANGLE_FAN,会出现左图图形:
此处的绘制方式如右图所示,可见顶点顺序对绘制有重要影响。
移动、旋转和缩放
相关内容:1.表达式方式进行仿射变换;2.变换矩阵进行仿射变换;3.将矩阵传递给uniform变量;4.按列主序
相关函数:gl.uniformMatrix4fv()小结:
本节通过表达式展示了仿射变换的坐标转换过程,主要为了引出变换矩阵。变换矩阵是常用的对图形处理的方法,多种变换能够糅合到一个矩阵中进行操作,对于代码编写非常遍历,当然也需要一定数学基础。许多语言对于矩阵运算都有额外的设计,这些设计大大提高了矩阵运算的效率,WebGL中也支持矩阵和矢量的运算,这大大提高了三维图像处理的效率。
本节用到的方法多为前面已经讲述过的内容,包括着色器中attribute变量和uniform变量、缓冲区对象的使用。关于矩阵的运算可以直接写在着色器语言中,不需要额外函数,构建矩阵除了类型化数组之外,还需要注意WebGL(OpenGL)中按列主序来保存内容。本节提到了一个新的函数来向unform传递矩阵数据。
从数据传递的过程可以看出,WebGL系统要求接收的数据一般需要严格定义类型,在传输的时候还需要告诉该系统使用方式,很多函数都是如此设计,以最新的函数gl.uniformMatrix4fv()为例,单看函数名,它传递的数据为float型数组,数组元素共4×4个,它告诉WebGL以4×4矩阵的方式使用该数组并将其赋值给uniform变量,传递数据的类型(数组)和使用数据的类型(矩阵)并不一致。
这一节有所局限的地方在于,所有的变换都是单一类型仅仅一步的变换,之后多半会提及的复杂类型的变换可能还涉及变换矩阵之间的运算,敬请期待。
本节将讨论如何移动(平移)、旋转和缩放三角形,这样的操作称为变换(transformations)或仿射变换(affine transformations)。
百度百科中对仿射变换的定义如下:
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。显而易见,相关的变换通过矩阵可以简单获得。
平移:
为了平移一个三角形,我们需要对顶点坐标的每个分量(x和y),加上三角形在对应轴(如X轴和Y轴)上平移的距离。
如,点p(x, y, z)平移到p’(x’, y’,z’),在X、Y、Z轴三个方向上平移的距离分别为Tx,Ty,Tz,其中的关系如下所示:
x ′ = x + T x y ′ = y + T y z ′ = z + T z x'=x+Tx\\ y'=y+Ty\\ z'=z+Tz x′=x+Txy′=y+Tyz′=z+Tz
- 显然,在WebGL系统中实现平移操作是一个逐顶点操作(per-vertex operation),我们需要在顶点着色器中为顶点坐标的每一个分量加上一个常量。
- 这一常量对于每个顶点都是一样的,故采用uniform变量即可。
该示例与HelloTriangle.js的差别有两处:
- 第一处在顶点着色器中,定义了uniform变量u_Translation作为平移量
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform vec4 u_Translation;\n' +
'void main(){\n' +
' gl_Position = a_Position + u_Translation;\n' +
'}\n'
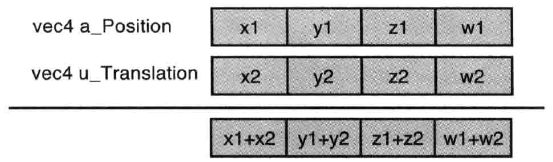
vec4变量加法如下图所示:
- 第二处在main()函数中,增加了uniform变量传值的过程
// 在x,y,z方向上平移的距离
var Tx = 0.5,
Ty = 0.5,
Tz = 0.5
// 将平移距离传输给顶点着色器uniform变量
let u_Translation = gl.getUniformLocation(gl.program, 'u_Translation')
if (!u_Translation) {
console.log('Failed to get the storage location of u_Translation')
}
gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0)
此处调用gl.uniform4f()而不是调用gl.uniform3f()是为了将齐次坐标第4分量设为0.0,防止加法使用后,将gl_Postion的第4分量变为1.0之外的数。
示例效果如下图所示:
完整的示例代码如下:
// TranslatedTriangle.js
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform vec4 u_Translation;\n' +
'void main(){\n' +
' gl_Position = a_Position + u_Translation;\n' +
'}\n'
// 片元着色器
var FSHADER_SOURCE =
'void main(){\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 在x,y,z方向上平移的距离
var Tx = 0.5,
Ty = 0.5,
Tz = 0.5
// 主函数
function main() {
// 获取canvas元素
let canvas = document.getElementById('webgl')
// 获取WebGL上下文
let gl = getWebGLContext(canvas)
if (!gl) {
console.log('Failed to get the rendering context for WebGL')
return
}
// 初始化着色器
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to initialize shaders')
return
}
// 设置顶点位置
let n = initVertexBuffers(gl)
if (n < 0) {
console.log('Failed to set the positions of the vertices')
return
}
// 将平移距离传输给顶点着色器uniform变量
let u_Translation = gl.getUniformLocation(gl.program, 'u_Translation')
if (!u_Translation) {
console.log('Failed to get the storage location of u_Translation')
}
gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0)
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空绘图区
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制三角形
gl.drawArrays(gl.TRIANGLES, 0, n)
}
function initVertexBuffers(gl) {
// 设置类型化数组和顶点数
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
let n = 3
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
// 绑定缓冲区
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
// 缓冲区写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STREAM_DRAW)
let a_Position = gl.getAttribLocation(gl.program, 'a_Position')
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position')
return -1
}
// 将缓冲区分配给attribute变量
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
// 开启attribute变量(连接)
gl.enableVertexAttribArray(a_Position)
return n
}
旋转:
读到此处,我们可以发现:WebGL顶点着色器只是简单地将顶点的位置记住,本身没有额外的计算能力;GLSL ES语言支持‘+’操作。
如平移,我们直接使用了加法得到位置,位置保存到顶点着色器之中,只是当作一个新的位置来存储而并不是调用函数来平移;
所以,此处的旋转应当类似,我们通过计算得到新的位置,再把位置传输给着色器中的变量。
描述平移,有以下三点需要指明:
- 旋转轴
- 旋转方向:逆时针或顺时针
- 旋转角度
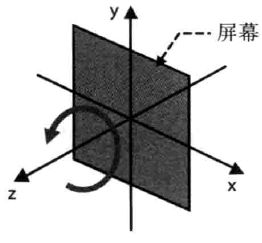
书中这样表述旋转操作:绕Z轴,逆时针旋转了β角度。关于“逆时针”的约定是:如果β是正值,观察者在Z轴正半轴某处,视线沿着Z轴负方向进行观察,看到的物体是逆时针旋转的,如下图所示。这种情况又可称作正旋转(positive rotation),这是本书中WebGL程序的默认设定,当然,β小于零代表顺时针旋转。
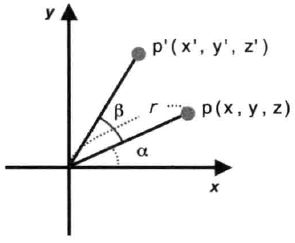
我们根据下图来计算p点(p向量)逆时针旋转β角度至p’点(p’向量),其坐标的变化规律:
从图中易知:
x = r cos α y = r sin α x ′ = r cos ( α + β ) y ′ = r sin ( α + β ) x=r\cos\alpha\\ y=r\sin\alpha\\ \\ x'=r\cos(\alpha+\beta)\\ y'=r\sin(\alpha+\beta) x=rcosαy=rsinαx′=rcos(α+β)y′=rsin(α+β)
根据三角函数变换,易知:
x ′ = x cos β − y sin β y ′ = x sin β + y cos β z ′ = z x'=x\cos\beta-y\sin\beta\\ y'=x\sin\beta+y\cos\beta\\ z'=z x′=xcosβ−ysinβy′=xsinβ+ycosβz′=z
关于sin()和cos()的计算,可以使用JavaScript内置的Math对象中sin()、cos()方法。
我们同样在HelloTriangle.js上进行改造来呈现旋转的效果:
- 顶点着色器部分进行改造,创建uniform变量u_CosB和u_SinB:(注意:vec4格式的数据与JavaScript中对象类似,每个数据都有索引)
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform float u_CosB, u_SinB;\n' +
'void main(){\n' +
' gl_Position.x = a_Position.x * u_CosB + a_Position.y * u_SinB;\n' +
' gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;\n' +
' gl_Position.z = a_Position.z;\n' +
' gl_Position.w = 1.0;\n' +
'}\n'
- 根据旋转角度计算三角函数,传递参数给uniform变量:(注意:JavaScript中Math.sin()和Math.cos()方法的参数为弧度制的角度。)
// 旋转角度
var ANGLE = 90.0
// 将旋转图形所需数据传输给顶点着色器
let radian = (Math.PI * ANGLE) / 180.0 // 转换为弧度制
let cosB = Math.cos(radian)
let sinB = Math.sin(radian)
let u_CosB = gl.getUniformLocation(gl.program, 'u_CosB')
let u_SinB = gl.getUniformLocation(gl.program, 'u_SinB')
if (!u_CosB) {
console.log('Failed to get the storage location of u_CosB')
}
if (!u_SinB) {
console.log('Failed to get the storage location of u_SinB')
}
gl.uniform1f(u_CosB, cosB)
gl.uniform1f(u_SinB, sinB)
示例呈现的效果如下图所示:
旋转示例TranslatedTriangle.js的完整代码如下:
// TranslatedTriangle.js
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform float u_CosB, u_SinB;\n' +
'void main(){\n' +
' gl_Position.x = a_Position.x * u_CosB + a_Position.y * u_SinB;\n' +
' gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;\n' +
' gl_Position.z = a_Position.z;\n' +
' gl_Position.w = 1.0;\n' +
'}\n'
// 片元着色器
var FSHADER_SOURCE =
'void main(){\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 旋转角度
var ANGLE = 90.0
// 主函数
function main() {
// 获取canvas元素
let canvas = document.getElementById('webgl')
// 获取WebGL上下文
let gl = getWebGLContext(canvas)
if (!gl) {
console.log('Failed to get the rendering context for WebGL')
return
}
// 初始化着色器
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to initialize shaders')
return
}
// 设置顶点位置
let n = initVertexBuffers(gl)
if (n < 0) {
console.log('Failed to set the positions of the vertices')
return
}
// 将旋转图形所需数据传输给顶点着色器
let radian = (Math.PI * ANGLE) / 180.0 // 转换为弧度制
let cosB = Math.cos(radian)
let sinB = Math.sin(radian)
let u_CosB = gl.getUniformLocation(gl.program, 'u_CosB')
let u_SinB = gl.getUniformLocation(gl.program, 'u_SinB')
if (!u_CosB) {
console.log('Failed to get the storage location of u_CosB')
}
if (!u_SinB) {
console.log('Failed to get the storage location of u_SinB')
}
gl.uniform1f(u_CosB, cosB)
gl.uniform1f(u_SinB, sinB)
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空绘图区
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制三角形
gl.drawArrays(gl.TRIANGLES, 0, n)
}
function initVertexBuffers(gl) {
// 设置类型化数组和顶点数
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
let n = 3
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
// 绑定缓冲区
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
// 缓冲区写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STREAM_DRAW)
let a_Position = gl.getAttribLocation(gl.program, 'a_Position')
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position')
return -1
}
// 将缓冲区分配给attribute变量
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
// 开启attribute变量(连接)
gl.enableVertexAttribArray(a_Position)
return n
}
变换矩阵对表达式方式的改造:
有过图像处理基础的读者应该知道,简单的仿射变换可以用数学表达式来实现,但当情形变得复杂时,表达式运算会相当繁琐,我们可以使用另一个数学工具——变换矩阵(Transformation matrix)。
变换矩阵涉及到矩阵运算,高等数学或线性代数中包含了此类知识,此处不再赘述,仅给出一组矩阵乘法的运算过程:
[ x ′ y ′ z ′ ] = [ a b c d e f g h i ] × [ x y z ] \begin{bmatrix}x' \\ y'\\ z'\end{bmatrix}=\begin{bmatrix}a&b&c \\d&e&f\\ g&h&i\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\end{bmatrix} ⎣⎡x′y′z′⎦⎤=⎣⎡adgbehcfi⎦⎤×⎣⎡xyz⎦⎤
x ′ = a x + b y + c z y ′ = d x + e y + f z z ′ = g x + h y + i z x'=ax+by+cz\\ y'=dx+ey+fz\\ z'=gx+hy+iz x′=ax+by+czy′=dx+ey+fzz′=gx+hy+iz
我们可以将之前的仿射变换通过变换矩阵的方式展示出来,如下:
旋转:改变换矩阵进行的变换是一次旋转,所以这个矩阵又可以称为旋转矩阵(rotation matrix)
[ x ′ y ′ z ′ ] = [ cos β − sin β 0 sin β cos β 0 0 0 1 ] × [ x y z ] \begin{bmatrix}x' \\ y'\\ z'\end{bmatrix}=\begin{bmatrix}\cos\beta&-\sin\beta&0 \\\sin\beta&\cos\beta&0\\ 0&0&1\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\end{bmatrix} ⎣⎡x′y′z′⎦⎤=⎣⎡cosβsinβ0−sinβcosβ0001⎦⎤×⎣⎡xyz⎦⎤
矩阵展开后为:
x ′ = x cos β − y sin β y ′ = x sin β + y cos β z ′ = z x'=x\cos\beta-y\sin\beta\\ y'=x\sin\beta+y\cos\beta\\ z'=z x′=xcosβ−ysinβy′=xsinβ+ycosβz′=z
平移:
平移和旋转的数学表达式如下:
x ′ = a x + b y + c z x ′ = x + T x x'=ax+by+cz\\ x'=x+Tx x′=ax+by+czx′=x+Tx
比较二者可以发现,如果a=1、b=0、c=0且增加一个分量,就可以用矩阵来表示平移。
矩阵增加一个分量后如下:
[ x ′ y ′ z ′ 1 ] = [ a b c d e f g h i j k l m n o p ] × [ x y z 1 ] \begin{bmatrix}x' \\ y'\\ z'\\1\end{bmatrix}=\begin{bmatrix}a&b&c&d \\e&f&g&h\\ i&j&k&l\\m&n&o&p\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\\1\end{bmatrix} ⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡aeimbfjncgkodhlp⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤
展开结果如下:
x ′ = a x + b y + c z + d y ′ = e x + f y + g z + h z ′ = i x + j y + k z + l 1 = m x + n y + o z + p x'=ax+by+cz+d\\ y'=ex+fy+gz+h\\ z'=ix+jy+kz+l\\ 1=mx+ny+oz+p x′=ax+by+cz+dy′=ex+fy+gz+hz′=ix+jy+kz+l1=mx+ny+oz+p
与平移表达式比较,可以简单得出a=0,b=0,c=0,d=Tx…等以此类推,可获得平移矩阵。
平移矩阵(translation matrix)如下:
[ x ′ y ′ z ′ 1 ] = [ 1 0 0 T x 0 1 0 T y 0 0 1 T z 0 0 0 1 ] × [ x y z 1 ] \begin{bmatrix}x' \\ y'\\ z'\\1\end{bmatrix}=\begin{bmatrix}1&0&0&Tx \\0&1&0&Ty\\ 0&0&1&Tz\\0&0&0&1\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\\1\end{bmatrix} ⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡100001000010TxTyTz1⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤
4×4旋转矩阵:
为了方便平移和旋转矩阵的融合,二者需要阶数相同,故需要将3×3的旋转矩阵转换为4×4的旋转矩阵。
以原来的旋转表达式为主,比较下面两组公式:
x ′ = x cos β − y sin β y ′ = x sin β + y cos β z ′ = z x ′ = a x + b y + c z + d y ′ = e x + f y + g z + h z ′ = i x + j y + k z + l 1 = m x + n y + o z + p x'=x\cos\beta-y\sin\beta\\ y'=x\sin\beta+y\cos\beta\\ z'=z\\ \\ x'=ax+by+cz+d\\ y'=ex+fy+gz+h\\ z'=ix+jy+kz+l\\ 1=mx+ny+oz+p x′=xcosβ−ysinβy′=xsinβ+ycosβz′=zx′=ax+by+cz+dy′=ex+fy+gz+hz′=ix+jy+kz+l1=mx+ny+oz+p
易知,在4×4的旋转矩阵中:a=cosβ,b=-sinβ,c=0,d=0…以此类推,4×4旋转矩阵为:
[ x ′ y ′ z ′ 1 ] = [ cos β − sin β 0 0 sin β cos β 0 0 0 0 1 0 0 0 0 1 ] × [ x y z 1 ] \begin{bmatrix}x' \\ y'\\ z'\\1\end{bmatrix}=\begin{bmatrix}\cos\beta&-\sin\beta&0&0 \\\sin\beta&\cos\beta&0&0\\ 0&0&1&0\\0&0&0&1\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\\1\end{bmatrix} ⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡cosβsinβ00−sinβcosβ0000100001⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤
RotatedTriangle_Matrix.js矩阵方式重写旋转示例与GLSL ES语言中的矩阵运算:
下面先给出RotatedTriangle_Matrix.js的完整代码:
// RotatedTriangle_Matrix.js
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform mat4 u_xformMatrix;\n' +
'void main(){\n' +
' gl_Position = u_xformMatrix * a_Position;\n' +
'}\n'
// 片元着色器
var FSHADER_SOURCE =
'void main(){\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 旋转角度
var ANGLE = 90.0
// 主函数
function main() {
// 获取canvas元素
let canvas = document.getElementById('webgl')
// 获取WebGL上下文
let gl = getWebGLContext(canvas)
if (!gl) {
console.log('Failed to get the rendering context for WebGL')
return
}
// 初始化着色器
if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
console.log('Failed to initialize shaders')
return
}
// 设置顶点位置
let n = initVertexBuffers(gl)
if (n < 0) {
console.log('Failed to set the positions of the vertices')
return
}
// 创建旋转矩阵
let radian = (Math.PI * ANGLE) / 180.0 // 转换为弧度制
let cosB = Math.cos(radian)
let sinB = Math.sin(radian)
// 注意WebGL中矩阵是列主序的
let xformMatrix = new Float32Array([
cosB, sinB, 0.0, 0.0,
-sinB, cosB, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0,
])
// 将旋转图形所需数据传输给顶点着色器
let u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix')
if (!u_xformMatrix) {
console.log('Failed to get the storage location of u_xformMatrix')
}
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix)
// 设置背景色
gl.clearColor(0.0, 0.0, 0.0, 1.0)
// 清空绘图区
gl.clear(gl.COLOR_BUFFER_BIT)
// 绘制三角形
gl.drawArrays(gl.TRIANGLES, 0, n)
}
function initVertexBuffers(gl) {
// 设置类型化数组和顶点数
let vertices = new Float32Array([0.0, 0.5, -0.5, -0.5, 0.5, -0.5])
let n = 3
// 创建缓冲区对象
let vertexBuffer = gl.createBuffer()
if (!vertexBuffer) {
console.log('Failed to create the buffer object')
return -1
}
// 绑定缓冲区
gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)
// 缓冲区写入数据
gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STREAM_DRAW)
let a_Position = gl.getAttribLocation(gl.program, 'a_Position')
if (a_Position < 0) {
console.log('Failed to get the storage location of a_Position')
return -1
}
// 将缓冲区分配给attribute变量
gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)
// 开启attribute变量(连接)
gl.enableVertexAttribArray(a_Position)
return n
}
代码运行结果如下:
相比于之前的旋转示例,运用矩阵的旋转示例有以下几点不同:
- 顶点着色器
// 顶点着色器
var VSHADER_SOURCE =
'attribute vec4 a_Position;\n' +
'uniform mat4 u_xformMatrix;\n' +
'void main(){\n' +
' gl_Position = u_xformMatrix * a_Position;\n' +
'}\n'
- mat4类型的变量是4×4的矩阵。
- WebGL顶点着色器中的’*'操作符支持矩阵乘法。着色器内置了常用的矢量和矩阵运算功能,我们可以用基本的操作符,如示例中出现过的‘+’和‘*’直接完成矢量和矩阵的运算,这种强大特性正是专为三维计算机图形学而设计的。
- 矩阵的设计
// 创建旋转矩阵
let radian = (Math.PI * ANGLE) / 180.0 // 转换为弧度制
let cosB = Math.cos(radian)
let sinB = Math.sin(radian)
// 注意WebGL中矩阵是列主序的
let xformMatrix = new Float32Array([
cosB, sinB, 0.0, 0.0,
-sinB, cosB, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0,
])
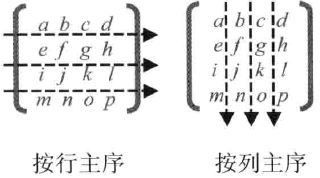
一般来说,我们有两种方式在数组中存储矩阵元素:按行主序(row major order)和按列主序(column major order),如下图所示:
WebGL与OpenGL一样,矩阵元素是按列主序存储在数组中的。如图中的矩阵存储在数组中的顺序就是这样的:[a, e, i, m, b, f, j, n, c, g, k, o, d, h, l, p]。示例中也是按这样的顺序存储在Float32Array数组中的。
- 向uniform变量传递矩阵
gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix)
该函数规范如下:
gl.uniformMatrix4fv(location, transpose, array):
将array表示的4×4矩阵分配给由location指定的uniform变量。
参数:
location:uniform变量的存储位置。
transpose:是否转置矩阵,在WebGL中没有转置矩阵的方法,必须指定为false。
array:待传输的类型化数组,4×4矩阵按列主序存储在其中。
返回值: 无
错误:
INVALID_OPERATION 不存在当前程序对象
INVALID_VALUE transpose不为false,或者数组的长度小于16。
矩阵重写平移:
与旋转矩阵类似,平移矩阵也可以通过:<新坐标> = <变换矩阵> * <旧坐标>的方式应用在着色器。二者仅在矩阵的内容方面有所不同:
// 平移距离
var Tx = 0.5,
Ty = 0.5,
Tz = 0.5
// 创建平移矩阵
let xformMatrix = new Float32Array([
1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
Tx, Ty, Tz, 1.0,
])
变换矩阵:缩放
有了之前两个变换矩阵的构建,缩放的矩阵就比较简单了,下面直接给出结论:
[ x ′ y ′ z ′ 1 ] = [ S x 0 0 0 0 S y 0 0 0 0 S z 0 0 0 0 1 ] × [ x y z 1 ] \begin{bmatrix}x' \\ y'\\ z'\\1\end{bmatrix}=\begin{bmatrix}Sx&0&0&0 \\0&Sy&0&0\\ 0&0&Sz&0\\0&0&0&1\end{bmatrix}\times\begin{bmatrix}x \\ y\\ z\\1\end{bmatrix} ⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡Sx0000Sy0000Sz00001⎦⎥⎥⎤×⎣⎢⎢⎡xyz1⎦⎥⎥⎤
Sx、Sy、Sz分别是图形在x、y、z轴方向上的缩放倍率,为1.0时保持不变,小于1则变小,大于1则变大。
我们修改上面示例的矩阵:
// 缩放
var Sx = 1.0,
Sy = 1.5,
Sz = 1.0
// 创建缩放矩阵
let xformMatrix = new Float32Array([
Sx, 0.0, 0.0, 0.0,
0.0, Sy, 0.0, 0.0,
0.0, 0.0, Sz, 0.0,
0.0, 0.0, 0.0, 1.0,
])
效果如下:
总结:
在这一章中,我们探索了如何将多个顶点的信息一次性地传入顶点着色器,如何利用顶点坐标按照不同的规则绘制图形,以及如何进行图形的变换。在前一章中我们只是绘制单个点,在这一章中我们绘制了三角形,但是这两章使用着色器的方式却是一致的。 此外,我们还学到了一些矩阵的知识,知道了如何使用矩阵对二维图形进行平移、旋转和缩放。虽然矩阵变换的知识稍稍有点复杂,但是它在三维计算机图形学中非常重要, 你应当做到对其了如指掌。