多路平衡归并+置换选择+最佳归并树
多路平衡归并+置换选择+最佳归并树
最近忙着考研,在学习复习数据结构(严慧敏版)外部排序那一章的时候简直开始怀疑人生了。以前我是怎么过来的?!败者树能吃吗??置换选择不就是操作系统页面换进换出的概念??TO YOUNG TOO SIMPLE SOMETIMES NAIVE !! 本文是个人对以上归并排序的三个算法的理解,如有错误请指出。好了废话少说,下面是正题。
众所周知,快速排序,希尔排序以及基数排序等内部排序算法只针对内存里的数据进行排序,也就是说如果要排序1G的数据就至少要分配1G的内存。当文件再大一点计算机就顶不住了,更别说现在都有蓝光A片了(好吧反正也不会蛋疼到对一部影视作品进行排序)
这时候归并排序就能排上用场了。我相信来看这篇小文的老哥小妹都已经懂得普通的2路归并排序了,我就直接从多路归并排序开始讲。
归并排序(k路)有以下几个特点:
- 输入是k个排好序的文件
- 算法对每个文件的操作是 顺序历遍(从左到右),并且只历遍一次
- 输出是1个排好序的文件
第一和第三个特点使得归并算法可以这样实现:每次读k个文件到内存,排好序,输出到一个文件,再重复操作。
但这样有个问题,k个小文件合并后的文件会越来越大,可以大到内存无法承受的程度。这时候第二个特点就发挥作用了。
顺序历遍一次允许我们将刚从文件里读进来的数据操作完成后立刻丢弃(释放内存)。
所以归并算法可以这样实现:维护固定大小的k个循环队列,对应于k个文件指针,每次从文件读进一个数据到队列覆盖以前的数据(因为以前的数据历遍完就没用了),操作完成后,循环队列的指针就往前走。所以文件流的输入操作和顺序历遍简直就是洛与霞好不!
这样一来归并排序就可以通过固定内存来完成外存文件的排序。
但是算法嘛,我们总得讲究时间复杂度。因为外存的读写速度远远慢与内存的读写速度,所以外部排序所需的时间主要取决于对外存的读写上。那么对外存的读取次数有影响的变量是什么呢?
试想要排序4个排好序的文件(这4个文件怎么来的先别管),如果是2路归并,那么就需要2趟,而每一趟都需要对文件进行一次历遍(也就是外存的读写)。但如果是4路归并,那么就只需要1趟,这样一来就减少了对外存的读写次数。
所以我们可以简单地认为:k路归并排序的k值越大,排序所需要时间越短。
试想一个大文件被均等分成4份,也就是有4个排好序的文件,对于2路归并,需要2趟。但如果这个大文件被分成2份,也就是有2个排好序的文件,同样是2路归并,则只需要1趟。
所以我们还可以简单地认为:初始归并段数(文件数)m越小,排序所需要时间越短。
根据不知是谁说的,归并次数(趟数)= logkm 。(具体证明自各儿看去)
所以要想提高k路归并排序的速度,有以下两个办法:
- 提高k值。对应于多路平衡归并算法。
- 降低m值。对应于置换选择算法。
哎呀,终于讲到主体了,心好累。。。
多路平衡归并算法
提高k值,看似简单却暗藏杀机。
看官们都知道,归并排序需要对每一路的当前值进行逐个比较,以得出最小值(或者最大值)。也就是说如果有k路,正常来说就需要比较k-1次(小丑鸭眉头一皱)。这种顺序比较成本太高了,那有没有什么方法可以降低成本呢?
废话,肯定有啊!那就是败者树。
什么是败者树?我打个比方吧,听说过高数没有?那就是一棵败者树,因为上面挂着很多人。。。(老子的高数就差那么两分)
也就是说,败者树的每一个节点都“挂着”失败者。所谓失败者,就是优先级没那么高的数据。
例如我想让数据从小到大排序,那么优先级比较高的自然就是较小的数。
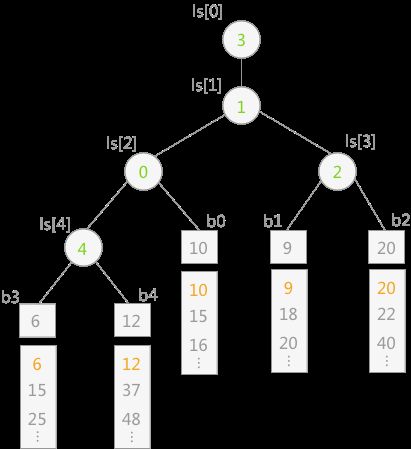
请允许老夫盗用一张图:
以上败者树的叶子节点存的是k路归并中的每一路在内存里的数据的最小值(循环队列里的当前值),非叶子节点存的是队列的下标。
败者树算法的主要过程是:把当前要比较的数字,从叶子结点的父节点到根节点,每次将要比较的数字和节点指向的队列的当前值比较,失败者(较大值)的下标留在节点里面,胜利者(较小值)继续往上比较,直到比较完根节点,得到最终胜利者。然后输出最终胜利者(最小值)并设置最终胜利者对应的队列的下一个数字作为下一次比较的初始值。
重复执行以上过程就得到了从小到大的合并段。
5路归并的比较算法如果采用顺序比较,需要4次比较才得到最小值;如果采用败者树算法,则最多需要3次。并且可以看出,k路归并对应的比较次数是大约是 log2k 次。
为什么败者树算法可以得到最小值?因为就算败者树的节点存的是失败者(的下标),但该失败者必定是该节点的某个孩子节点的胜利者。也就是说,当有一个数字过关斩将来到父节点时,它所面对的是该父节点的另外一个孩子的最小值,这就间接地和另外一个孩子所能索引到的所有队列的最小值比较了。
置换选择算法
到此为止,我们都是在假设已经有了排好序的初始归并段(文件)的前提下进行讨论的。
为了得到初始归并段,我们可以把大文件分成内存所能承受的若干个文件,然后把文件逐个从外存读进内存,进行某种内部排序算法(快排,希尔等),再输出到单个文件。但由于内存的限制,大文件往往要分成很多很多很多个小文件。但是因为初始归并段的个数越大,排序所需时间越长。然而置换选择算法就很好地解决了这个问题。
置换选择算法使用的数据结构也是败者树。
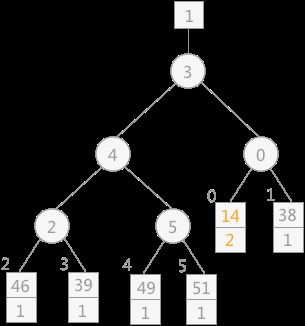
请再次允许老夫盗用一张图:
由图可见,置换选择算法的叶子结点存的就不只是数据了,还包括一个序号。并且非叶子节点存的不再是队列的下标,而是数组的下标。
总体过程是,先用一个数组存放从大文件里读进来的数字,然后建立败者树,每次读进一个数字就更新败者树并输出最终胜利者。
但这棵败者树的比较和前面的多路平衡归并有一点不同的地方:先比较序号,序号较小的数字胜出;如果序号相等,数值较小的数字胜出。当得到最终胜利者并将要输出到文件的时候,需要判断一下序号是否和前一个最终胜利者相等,相等就直接输出,不相等就输出到另一个文件(也就是开始构建新的初始段)。并且,如果从文件读进来的数字比上个最终胜利者大,那么设置序号和最终胜利者的序号相等,否则序号等于最终胜利者的序号加一。
原理是什么?可以这样考虑:首先,在序号相等的情况下,最终胜利者的前一个的值肯定比后一个的值要小。如果序号不相等,就不可能存放在同一个初始段(文件)。这保证了初始段的顺序问题。其次,有没有可能在败者树里面出现至少3个不同序号的数据(最终胜利者是较大的序号的数)?不可能。因为败者树的当前节点可以间接地和其它所有节点比较,所以如果当前败者树存在不同序号的数据,那么比较到最后,肯定是序号较小的数据胜出。也就是说,只有当较小序号的数据全部输出完成,才有可能插入更大序号的数据。最终的结果是,置换选择算法一段接着一段地输出排好序的文件段。
注意这些文件段的数据个数不一定相同,但肯定大于等于败者树的叶子结点的个数。因为一个段最坏情况是每次读进的数字都比上一个最终胜利者的值要小,序号设为较大值。这样每读入一个数字,序号较小值的叶子结点就减少一个,到最后输出一个数据长度等于败者树叶子结点个数的文件段。
最佳归并树
累死了。
由于初始归并段的长度不相等,那么归并段的归并顺序会不会对排序的时间有影响?
可以这样考虑:
- 相同初始归并段数,对于不同的归并顺序,会有相同的归并次数。(归并一次,段数少一)
- 当前归并段的长度 = 两个子归并段长度相加。同时,子归并段的长度越长,归并时间越长。
也就是说如果一开始就归并很长的段,由于该段还会在以后的归并中出现,那么消耗的时间就很长了。所以我们应该先归并段长较短的段。
假如有三个初始归并段,段长分别为:1, 2, 3。
先归并2和3,再归并1和5,所需时间:(2+3)+(2+3+1) = 11 。
先归并1和2,再归并3和3,所需时间:(1+2)+(1+2+3) = 9。
所以可以通过构造哈夫曼树的方法得出最佳归并顺序,具体过程我就不赘述了。