怒刷LeetCode的第21天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:哈希表
方法二:计数器数组
第二题
题目来源
题目内容
解决方法
方法一:分治法
方法二:快速幂 + 迭代
方法三:快速幂 + 递归
第三题
题目来源
题目内容
解决方法
方法一:回溯算法
方法二:基于集合的回溯
方法三:基于位运算的回溯
方法四:DFS(深度优先搜索)
第一题
题目来源
49. 字母异位词分组 - 力扣(LeetCode)
题目内容
解决方法
方法一:哈希表
思路: 首先,我们可以使用哈希表来存储字母异位词分组的结果。遍历字符串数组中的每个字符串,对每个字符串进行排序,得到其排序后的字符串作为哈希表的键。然后将原始字符串添加到对应键的列表中,最后返回哈希表的值即可。
import java.util.*;
class Solution {
public List> groupAnagrams(String[] strs) {
// 创建一个哈希表,key 为排序后的字符串,value 为相同排序后字符串的原始字符串列表
Map> map = new HashMap<>();
// 遍历字符串数组
for (String str : strs) {
// 将字符串转为字符数组并排序
char[] arr = str.toCharArray();
Arrays.sort(arr);
String sortedStr = String.valueOf(arr);
// 如果哈希表中不存在该键,则新建一个键值对
if (!map.containsKey(sortedStr)) {
map.put(sortedStr, new ArrayList<>());
}
// 将原始字符串添加到对应键的列表中
map.get(sortedStr).add(str);
}
// 返回哈希表的值,即分组后的结果列表
return new ArrayList<>(map.values());
}
}
复杂度分析:
时间复杂度分析:
- 对于每个字符串,需要将其排序,排序的时间复杂度为 O(klogk),其中 k 为字符串的长度。
- 总共有 n 个字符串,因此总时间复杂度为 O(nklogk)。
空间复杂度分析:
- 使用了一个哈希表来存储分组的结果,最多包含 n 个键值对。
- 每个键值对中的值是一个列表,列表的最大长度为 n。
- 因此,空间复杂度为 O(n)。
综上所述,该解法的时间复杂度为 O(nklogk),空间复杂度为 O(n)。
LeetCode运行结果:
方法二:计数器数组
除了使用哈希表的方法,我们还可以通过使用计数器数组来实现字母异位词的分组。
具体思路如下:
- 创建一个长度为26的整型数组count,用于记录每个字母出现的次数。
- 遍历字符串数组中的每个字符串:
- 将count数组每个位置的值都置为0,用于统计当前字符串的字符出现次数。
- 遍历当前字符串,将每个字符出现的次数加到count数组对应的位置上。
- 将count数组转换为一个唯一的字符串作为哈希表的键。
- 将当前字符串添加到对应键的列表中。
- 返回哈希表的值,即分组后的结果列表。
import java.util.*;
class Solution {
public List> groupAnagrams(String[] strs) {
// 创建一个哈希表,key 为唯一的计数器字符串,value 为相同计数器字符串的原始字符串列表
Map> map = new HashMap<>();
// 遍历字符串数组
for (String str : strs) {
// 创建一个长度为26的计数器数组
int[] count = new int[26];
// 统计当前字符串中每个字符出现的次数
for (char c : str.toCharArray()) {
count[c - 'a']++;
}
// 将计数器数组转换为一个唯一的字符串作为哈希表的键
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 26; i++) {
sb.append('#');
sb.append(count[i]);
}
String key = sb.toString();
// 如果哈希表中不存在该键,则新建一个键值对
if (!map.containsKey(key)) {
map.put(key, new ArrayList<>());
}
// 将原始字符串添加到对应键的列表中
map.get(key).add(str);
}
// 返回哈希表的值,即分组后的结果列表
return new ArrayList<>(map.values());
}
}
复杂度分析:
时间复杂度分析:
- 对于每个字符串,需要遍历一次,并统计字符出现的次数,时间复杂度为 O(k)。
- 总共有 n 个字符串,因此总时间复杂度为 O(nk)。
空间复杂度分析:
- 使用了一个哈希表来存储分组的结果,最多包含 n 个键值对。
- 每个键值对中的值是一个列表,列表的最大长度为 n。
- 因此,空间复杂度为 O(n)。
综上所述,该解法的时间复杂度为 O(nk),空间复杂度为 O(n)。
LeetCode运行结果:
第二题
题目来源
50. Pow(x, n) - 力扣(LeetCode)
题目内容
解决方法
方法一:分治法
根据题目要求,可以使用分治法来实现 pow(x, n) 函数。具体做法如下:
- 若 n < 0,则转换为求解 pow(1/x, -n)。
- 定义递归函数 helper(x, n),表示计算 x 的整数 n 次幂。
- 当 n 为 0 时,返回 1。
- 当 n 为偶数时,将问题规模缩小一半,即计算 helper(x, n/2) * helper(x, n/2)。
- 当 n 为奇数时,将结果乘以 x,即计算 x * helper(x, n/2) * helper(x, n/2)。
- 根据 n 的正负性,返回最终结果。
public class Solution {
public double myPow(double x, int n) {
// 若指数 n 为负数,则转换为求解 pow(1/x, -n)
if (n < 0) {
x = 1 / x;
n = -n;
}
return helper(x, n);
}
private double helper(double x, int n) {
// 递归结束条件:n 为 0
if (n == 0) {
return 1.0;
}
// 递归计算一半的结果
double half = helper(x, n / 2);
// 若 n 为偶数
if (n % 2 == 0) {
return half * half;
}
// 若 n 为奇数
else {
return x * half * half;
}
}
}
复杂度分析:
时间复杂度分析:
- 每次递归,问题规模缩小一半,因此递归的层数为 O(logn)。
- 在每一层递归中,需要进行一次乘法运算。因此,总时间复杂度为 O(logn)。
空间复杂度分析:
- 使用了 O(logn) 的递归栈空间。
LeetCode运行结果:
方法二:快速幂 + 迭代
算法思路: 首先,将指数 n 转化为 long 类型的 N,以处理负数指数的情况。 然后,对于任意一个实数 x 和非负整数 N,可以通过二分法迭代计算出 x^N 的值。
假设已经计算出 x^{N/2},那么有以下两种情况:
当 N 为偶数时,有:x^N = (x^{N/2})^2 当 N 为奇数时,有:x^N = x * (x^{N/2})^2
通过上面两种情况,可以将原问题分解成规模更小的子问题,并且每次只需进行一次乘法运算即可。不断重复这个过程,最终可以得到 x^N 的值。
class Solution {
public double myPow(double x, int n) {
// 将指数转化为long类型的N,以处理负数指数的情况
long N = n;
// 如果N为负数,将x变为1/x,指数变为相反数
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
public double quickMul(double x, long N) {
// ans初始化为1,因为x^0=1
double ans = 1.0;
// 贡献的初始值为x
double x_contribute = x;
// 使用二分法迭代计算x^N
while (N > 0) {
// 如果N的二进制最低位为1,那么需要计入贡献
if (N % 2 == 1) {
ans *= x_contribute;
}
// 将贡献不断平方
x_contribute *= x_contribute;
// 右移一位,相当于除以2
N /= 2;
}
return ans;
}
}
复杂度分析:
- 时间复杂度:由于每次将指数减半,因此算法的迭代次数为 logn。每次迭代只需要进行一次乘法运算,因此总时间复杂度为 O(logn)。
- 空间复杂度:算法中只使用了常数个变量,因此空间复杂度为 O(1)。
LeetCode运行结果:
方法三:快速幂 + 递归
算法思路: 假设已经计算出 x^{N/2},那么有以下两种情况:
当 N 为偶数时,有:x^N = (x^{N/2})^2 当 N 为奇数时,有:x^N = x * (x^{N/2})^2
通过上面两种情况,可以将原问题分解成规模更小的子问题,并且每次只需进行一次乘法运算即可。不断重复这个过程,最终可以得到 x^N 的值。
class Solution {
public double myPow(double x, int n) {
// 将指数转化为long类型的N,以处理负数指数的情况
long N = n;
// 如果N为负数,将x变为1/x,指数变为相反数
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
public double quickMul(double x, long N) {
// 如果N==0,返回1.0
if (N == 0) {
return 1.0;
}
// 先计算出x的N/2次方
double y = quickMul(x, N / 2);
// 如果N为偶数,y*y即为x的N次方
if (N % 2 == 0) {
return y * y;
}
// 如果N为奇数,y*y*x即为x的N次方
else {
return y * y * x;
}
}
}
复杂度分析:
- 时间复杂度:由于每次将指数减半,因此算法的迭代次数为 logn。每次迭代只需要进行一次乘法运算,因此总时间复杂度为 O(logn)。
- 空间复杂度:由于算法使用了递归来实现快速幂运算,因此最坏情况下递归的深度为 logn,因此空间复杂度为 O(logn)。
LeetCode运行结果:
第三题
题目来源
51. N 皇后 - 力扣(LeetCode)
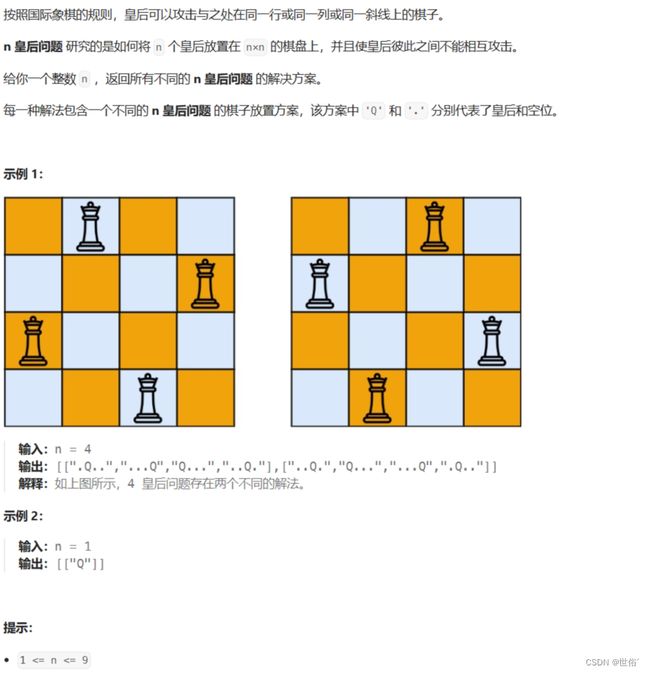
题目内容
解决方法
方法一:回溯算法
N 皇后问题可以使用回溯算法来求解。回溯算法是一种深度优先搜索的算法,通过递归地尝试所有可能的解决方案,并在不满足条件时进行回溯。
具体思路如下:
- 创建一个长度为
n的数组queens,用于存储每一行皇后所在的列索引。初始化时,所有元素都为-1,表示还没有放置皇后。 - 使用回溯函数进行递归搜索,函数定义如下:
- 参数
row表示当前正在放置皇后的行数。 - 参数
n表示棋盘的大小,也表示需要放置的皇后的数量。 - 在递归的过程中,从左到右依次尝试放置皇后,对于每个位置
(row, col),判断是否可以放置皇后的条件是不在同一列或同一斜线上。如果可以放置,则将queens[row]设置为col,表示在当前行放置皇后的位置为(row, col)。 - 如果当前行是最后一行(即
row == n - 1),说明找到了一种解法,将该解法存储起来。 - 如果当前行不是最后一行,则继续递归放置下一行的皇后。
- 在递归结束后,需要进行回溯操作,即撤销当前行放置的皇后,尝试放置下一个位置。
- 参数
- 创建一个函数
isValid(row, col, n)来判断当前位置是否可以放置皇后。判断的条件是不在同一列或同一斜线上。具体判断方法如下:- 对于每一行,使用数组
queens存储了已经放置的皇后位置,因此只需要判断列号是否相等或者斜率是否为 ±1±1 即可。
- 对于每一行,使用数组
- 最后,将所有解法转换为字符串表示,存储到结果列表中,并返回作为结果。
class Solution {
// 存储每一行皇后所在的列索引
int[] queens;
// 存储所有解法
List> solutions;
public List> solveNQueens(int n) {
queens = new int[n];
solutions = new ArrayList<>();
backtrack(0, n);
return solutions;
}
// 回溯函数
private void backtrack(int row, int n) {
if (row == n) { // 找到一种解法
List solution = generateSolution(n);
solutions.add(solution);
} else {
for (int col = 0; col < n; col++) {
if (isValid(row, col, n)) { // 判断当前位置是否可以放置皇后
queens[row] = col;
backtrack(row + 1, n); // 继续下一行的回溯
}
}
}
}
// 判断当前位置是否可以放置皇后
private boolean isValid(int row, int col, int n) {
for (int i = 0; i < row; i++) {
int diff = Math.abs(col - queens[i]);
if (diff == 0 || diff == row - i) { // 判断是否在同一列或同一斜线上
return false;
}
}
return true;
}
// 生成解法的字符串表示
private List generateSolution(int n) {
List solution = new ArrayList<>();
for (int row = 0; row < n; row++) {
StringBuilder sb = new StringBuilder();
for (int col = 0; col < n; col++) {
if (col == queens[row]) {
sb.append("Q");
} else {
sb.append(".");
}
}
solution.add(sb.toString());
}
return solution;
}
}
复杂度分析:
- 时间复杂度:在回溯算法中,对于每一行的每一个位置,都需要进行判断。在判断当前位置是否可以放置皇后时,需要遍历已经放置的皇后,时间复杂度为 O(N)。因此,在放置 N 个皇后的过程中,总体的时间复杂度为 O(N^N \cdot N!),其中 N! 表示 N 的阶乘。
- 空间复杂度:除了存储结果的列表之外,需要额外使用一个数组 queens 来存储每一行皇后所在的列索引,数组的长度为 N。递归调用栈的最大深度为 N。因此,额外的空间复杂度为 O(N)。
需要注意的是,以上复杂度分析是在没有剪枝优化的情况下。实际上,N 皇后问题可以通过剪枝优化来减少搜索的空间和时间复杂度,例如通过判断不同行上皇后的冲突情况,来排除不必要的搜索路径。通过合理的剪枝策略,可以显著提高算法的效率。
总结起来,N 皇后问题的时间复杂度为 O(N^N \cdot N!),空间复杂度为 O(N)。
LeetCode运行结果:
方法二:基于集合的回溯
import java.util.*;
class Solution {
public List> solveNQueens(int n) {
List> result = new ArrayList<>();
Set cols = new HashSet<>();
Set diagonals1 = new HashSet<>();
Set diagonals2 = new HashSet<>();
backtrack(n, 0, new ArrayList<>(), result, cols, diagonals1, diagonals2);
return result;
}
private void backtrack(int n, int row, List board, List> result,
Set cols, Set diagonals1, Set diagonals2) {
if (row == n) {
result.add(new ArrayList<>(board));
return;
}
for (int col = 0; col < n; col++) {
int diagonal1 = row - col;
int diagonal2 = row + col;
if (cols.contains(col) || diagonals1.contains(diagonal1) || diagonals2.contains(diagonal2)) {
continue;
}
cols.add(col);
diagonals1.add(diagonal1);
diagonals2.add(diagonal2);
char[] charArray = new char[n];
Arrays.fill(charArray, '.');
charArray[col] = 'Q';
String rowString = new String(charArray);
board.add(rowString);
backtrack(n, row + 1, board, result, cols, diagonals1, diagonals2);
board.remove(board.size() - 1);
cols.remove(col);
diagonals1.remove(diagonal1);
diagonals2.remove(diagonal2);
}
}
} 通过回溯的方式,在每一行中的每个位置尝试放置皇后。使用三个集合 cols、diagonals1 和 diagonals2 分别记录已经放置的皇后所在的列、主对角线和副对角线的信息,用于判断是否是合法的放置位置。当放置的皇后数量达到 N 个时,将当前结果加入最终的结果列表中。
注意,在每一次放置皇后之前,需要先判断当前位置是否已经被占据,如果是,则跳过该位置。同时,在回溯的过程中,需要及时撤销之前的操作,即从集合和棋盘中移除皇后的相关信息。
复杂度分析:
N 皇后问题的时间复杂度很难精确地确定,因为不同的搜索方案具有不同的耗时。但是可以确定的是,N 皇后问题解的数量一定是阶乘级别的,即 O(N!)。
在回溯算法中,每次递归处理到第 i 行时,都需要考虑所有列 j 是否可用,因此时间复杂度为 O(N^i)。因此,总的时间复杂度可以表示为: O(N!)
空间复杂度方面,除了存储答案和一些辅助变量外,主要的空间开销是递归调用栈的空间。在最坏情况下,即所有可能的排列方式都需要尝试一遍时,递归栈的深度会达到 N,每层递归需要 O(N) 的空间,因此空间复杂度也是 O(N)。
需要注意的是,在实际应用中,我们可以通过剪枝等方式来优化回溯算法的效率,从而在适当的情况下减小时间和空间的开销。
LeetCode运行结果:
方法三:基于位运算的回溯
当使用位运算来解决 N 皇后问题时,可以通过一个整数的二进制表示来记录每个皇后的位置,其中每个皇后占据一列,皇后所在的行由二进制中的位置表示。
class Solution {
public List> solveNQueens(int n) {
List> result = new ArrayList<>();
solveNQueensHelper(n, 0, 0, 0, 0, new ArrayList<>(), result);
return result;
}
private void solveNQueensHelper(int n, int row, int col, int ld, int rd, List solution, List> result) {
// 找到一个可行解
if (row == n) {
result.add(new ArrayList<>(solution));
return;
}
// 生成当前行的可选位置
int availablePositions = ((1 << n) - 1) & (~(col | ld | rd));
// 在当前行逐个尝试可选位置
while (availablePositions != 0) {
int position = availablePositions & (-availablePositions); // 获取最低位的 1
int columnIndex = Integer.bitCount(position - 1); // 获取最低位的 1 所在的列索引
// 构建当前行的字符串表示
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) {
sb.append(i == columnIndex ? 'Q' : '.');
}
solution.add(sb.toString());
// 更新下一行的状态
solveNQueensHelper(n, row + 1, col | position, (ld | position) << 1, (rd | position) >> 1, solution, result);
// 恢复当前行的状态
solution.remove(solution.size() - 1);
// 清除最低位的 1,继续尝试下一个可选位置
availablePositions &= (availablePositions - 1);
}
}
} 这段代码中,使用位运算来记录每个皇后的位置,其中 col 表示已占据的列,ld 表示已占据的左对角线,rd 表示已占据的右对角线。通过位运算可以快速判断某个位置是否可选。
在 solveNQueensHelper 方法中,递归地尝试每个可选位置,并更新下一行的状态。当找到一个可行解时,将其添加到结果列表中。最后,将整个结果返回。
复杂度分析:
时间复杂度:
- 构建可选位置集合的操作需要遍历每个列,时间复杂度为 O(N)。
- 在递归求解过程中,每行都需要尝试遍历可选位置,时间复杂度为 O(N!)。 综上,总的时间复杂度为 O(N * N!)。
空间复杂度:
- 递归调用栈的深度为 N,每层递归需要常数级别的额外空间,因此空间复杂度为 O(N)。
- 存储结果列表的空间复杂度为 O(N^2 * N!),其中 N^2 是存储每个解所需的空间。 综上,总的空间复杂度为 O(N^2 * N!).
需要注意的是,虽然使用位运算可以提高算法的执行效率,但是在 N 很大时,N 皇后问题仍然是一个非常耗时的问题。因此,在实际应用中,当 N 较大时,可能需要考虑其他更加高效的解决方案。
LeetCode运行结果:
方法四:DFS(深度优先搜索)
import java.util.ArrayList;
import java.util.List;
class Solution {
public List> solveNQueens(int n) {
List> result = new ArrayList<>();
boolean[] colUsed = new boolean[n];
boolean[] diag1Used = new boolean[2 * n - 1];
boolean[] diag2Used = new boolean[2 * n - 1];
char[][] board = new char[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i][j] = '.';
}
}
dfs(0, n, board, colUsed, diag1Used, diag2Used, result);
return result;
}
private void dfs(int row, int n, char[][] board, boolean[] colUsed, boolean[] diag1Used, boolean[] diag2Used, List> result) {
// 找到一个可行解
if (row == n) {
List solution = new ArrayList<>();
for (int i = 0; i < n; i++) {
solution.add(new String(board[i]));
}
result.add(solution);
return;
}
for (int col = 0; col < n; col++) {
int diag1 = row + col;
int diag2 = row - col + n - 1;
// 检查当前位置是否可放置皇后
if (!colUsed[col] && !diag1Used[diag1] && !diag2Used[diag2]) {
board[row][col] = 'Q';
colUsed[col] = true;
diag1Used[diag1] = true;
diag2Used[diag2] = true;
// 继续搜索下一行
dfs(row + 1, n, board, colUsed, diag1Used, diag2Used, result);
// 恢复当前位置的状态
board[row][col] = '.';
colUsed[col] = false;
diag1Used[diag1] = false;
diag2Used[diag2] = false;
}
}
}
} 在这段代码中,我们使用 boolean 数组来表示每一列、每一条正对角线和反对角线是否已经被占用。我们使用二维字符数组来表示棋盘,其中皇后的位置用 'Q' 表示,空位置用 '.' 表示。
在 solveNQueens 方法中,首先初始化棋盘和状态数组,然后调用 dfs 方法进行深度优先搜索。
dfs 方法采用递归的方式,从第 0 行开始,逐行遍历每个位置。对于每个位置,检查当前列、正对角线和反对角线是否已经被占用。如果没有被占用,则将皇后放在该位置,并更新状态数组。然后递归地搜索下一行。当搜索到最后一行时,得到一个可行解,将其保存到结果列表中。最后,恢复当前位置的状态,继续尝试下一个位置。
复杂度分析:
时间复杂度:
- 在递归求解过程中,每行都需要尝试遍历可选位置,时间复杂度为 O(N!)。
- 在每个位置上,需要检查当前列、正对角线和反对角线是否已经被占用,每次检查的时间复杂度为 O(1)。 综上,总的时间复杂度为 O(N * N!).
空间复杂度:
- 递归调用栈的深度为 N,每层递归需要常数级别的额外空间,因此空间复杂度为 O(N)。
- 存储结果列表的空间复杂度为 O(N^2 * N!),其中 N^2 是存储每个解所需的空间。 综上,总的空间复杂度为 O(N^2 * N!).
需要注意的是,尽管在代码中使用了剪枝操作来减少不必要的搜索,但是对于较大的 N,仍然会有大量的组合需要尝试。因此,在实际应用中,当 N 较大时,可能需要考虑其他更加高效的解决方案或优化算法。
LeetCode运行结果: