面试高频考点 -- 常见的排序算法(7种)
目录
- 1. 直接插入排序
- 2. 希尔排序
- 3. 选择排序
- 4. 堆排序（重要）
- 5. 冒泡排序（加优化）
- 6. 快速排序（重要）
- 7. 归并排序（重要）
常见排序：
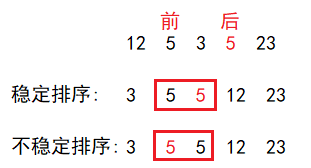
稳定性
两个相等的数据，如果经过排序后，排序算法能保证其相对位置不发生变化。
例如：
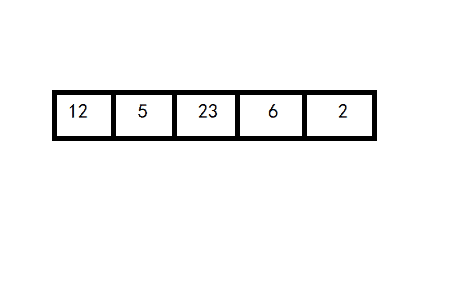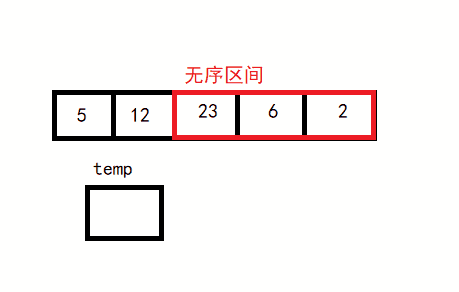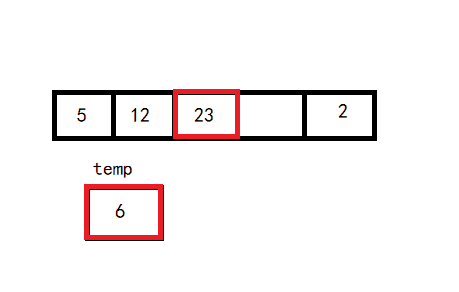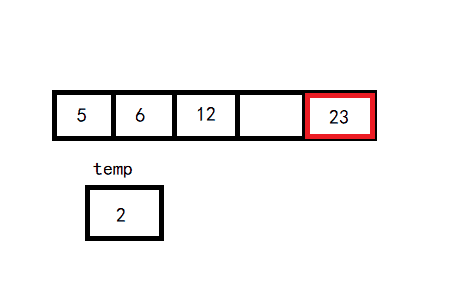
1. 直接插入排序
从第二个元素开始往后，每次选择一个元素，当前元素前面的区间就是一个有序区间，后面就是无序区间。每次选择无序区间的第一个元素，在有序区间内选择合适的位置插入。
排序12 5 23 6 2
直至整个数组变为有序区间。
/**
* 时间复杂度： O(N^2)
* 空间复杂度： O(1)
* 稳定性： 稳定
* @param arr
*/
public void insertSort(int[] arr){
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];
int j = i-1;
for (; j >= 0; j--) {
if(arr[j] > temp){
// 大于 temp，就向后移
arr[j+1] = arr[j];
}else {
// 找到适合的位置，不用再往前找了，直接退出循环
break;
}
}
//给找到的位置赋值
arr[j+1] = temp;
}
}
可以看出，当数据越趋近于有序，退出循环就越快，排序的速度也越快，所以 数据越有序，排序的效率越高。
- 时间复杂度：
- 最坏情况 O(N^2)
- 最好情况 O(N) (数组原本就有序)
- 空间复杂度： O(1)
- 稳定性： 稳定
2. 希尔排序
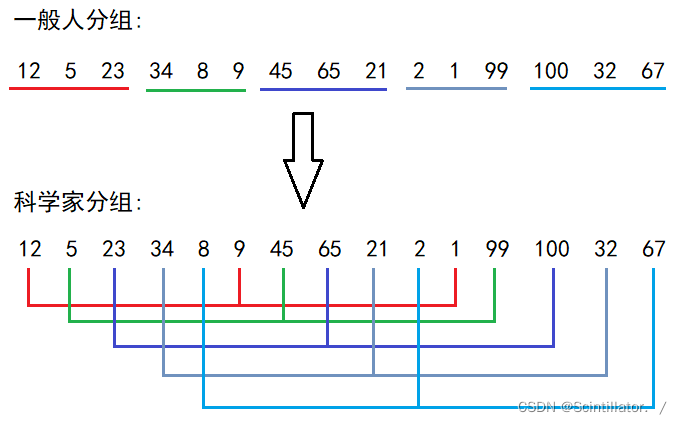
将一组数据分为 n 组，每组进行直接插入排序，然后缩小 n 的值，直到n变成1，在每次分组之后，因为进行过排序，每组的的数据会越来越有序， 而直接插入排序 数据越有序，排序的效率越高。 所以会越来越快。
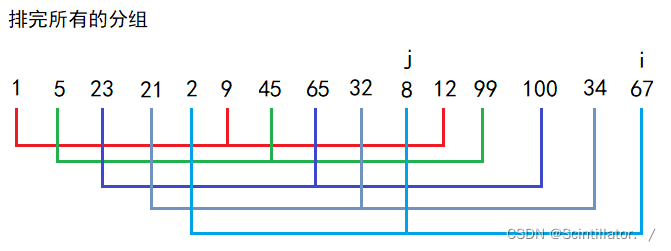
那么希尔排序怎么进行分组呢？假设将以下数据分为5组
直到i走到最后一个元素的位置
/**
* 时间复杂度： O(n^1.3 ~ n^1.5)
* 空间复杂度： O(1)
* 稳定性： 不稳定
* @param arr
*/
public void shell(int[] arr){
int gap = arr.length;// 最大的组数
while (gap > 1){
// 传入每次的组数
shell(arr,gap);
// 这里的分组每次除以 2
gap /= 2;
}
//最后看做一组进行排序
shell(arr,1);
}
// 对分的组数进行直接插入排序
public void shell(int[] arr,int gap){
int right = gap;
while (right < arr.length){
int left = right - gap;
int temp = arr[right];
while (left >= 0){
if (arr[left] > temp){
arr[left + gap] = arr[left];
left -= gap;
}else {
break;
}
}
arr[left + gap] = temp;
right++;
}
}
- 时间复杂度： O(n^1.3 ~ n^1.5)
- 空间复杂度： O(1)
- 稳定性： 不稳定
3. 选择排序
每一次从无序区间 选出最大(或最小) 的一个元素，存放在无序区间的最后（或最前），直到全部待排序的数据元素排完。
/**
* 时间复杂度： O(n^2)
* 空间复杂度： O(1)
* 稳定性： 不稳定
*/
public void selectSort(int[] arr){
for (int start = 0; start < arr.length; start++) {
int minIndex = start;
for (int i = start+1; i < arr.length; i++) {
// 找到最小值下标
if (arr[minIndex] > arr[i]){
minIndex = i;
}
}
// 交换无序区间第一个值和当前无序区间最小值
int temp = arr[start];
arr[start] = arr[minIndex];
arr[minIndex] = temp;
}
}
- 时间复杂度： O(n^2)
- 空间复杂度： O(1)
- 稳定性： 不稳定
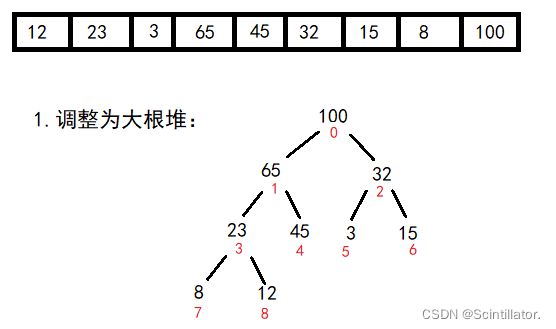
4. 堆排序（重要）
- 根据数组数据建立大根堆（详见: 堆的应用）
- 调整每一棵子树
- 每颗子树变成大根堆（向下调整）
- 数组排序
- 交换无序区间第一个位置（0）和最后一个位置的值（end）
- end-- ，剩下的无序区间再调整为大根堆，直到end来到0位置，数组整个有序
/**
* 时间复杂度： O(n * logN)
* 空间复杂度： O(1)
* 稳定性： 不稳定
*/
public void heapSort(int[] arr){
// 将数组变为大根堆
createHeap(arr);
int end = arr.length-1;
while (end > 0){
// 交换最后一个位置和第一个位置上的值
int temp = arr[end];
arr[end] = arr[0];
arr[0] = temp;
// 向下调整变成大根堆
shiftDown(arr,0,end);
// end--
end--;
}
}
// 建立大根堆
public void createHeap(int[] arr){
// 得到最后一颗子树的根节点
int parent = (arr.length-1-1)/2;
// 向上调整直到来到根节点
for (int i = parent; i >= 0; i--) {
shiftDown(arr,i,arr.length);
}
}
// 向下调整
public void shiftDown(int[] arr,int parent,int end){
int child = 2*parent+1;
while (child < end){
// 找到较大的孩子
if (child+1 < end && arr[child] < arr[child+1]){
child = child+1;
}
// 孩子更大，交换
if (arr[parent] < arr[child]){
int temp = arr[parent];
arr[parent] = arr[child];
arr[child] = temp;
parent = child;
child = 2*parent + 1;
}else {
// 不需要交换，直接退出
break;
}
}
}
- 时间复杂度： O(n * logN)
- 空间复杂度： O(1)
- 稳定性： 不稳定
5. 冒泡排序（加优化）
在无序区间，通过相邻数的比较，将最大的数冒泡到无序区间的最后，持续这个过程，直到数组整体有序。
可以看到，当第一轮比较结束后，最大数12被放在了数组最后，即12正确的位置，有序区间变为12，无序区间为前面部分，继续比较，直到整个数组变为有序。
/**
* 时间复杂度： O(n^2)
* 空间复杂度： O(1)
* 稳定性： 稳定
*/
public void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
// 定义一个标志位，判断是否已经有序了
// 若没有发生交换，则已经有序了，直接退出
boolean flag = true;
for (int j = 0; j < arr.length-1-i; j++) {
// 当 j 大于 j+1，交换，将较大值换到后面去
if (arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
flag = false;
}
}
if (flag) {
// 没发生过交换
break;
}
}
}
- 时间复杂度：
- 最坏情况 O(N^2)
- 最好情况 O(N) (一趟就有序了)
- 空间复杂度： O(1)
- 稳定性： 稳定
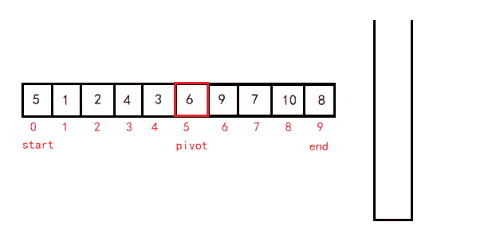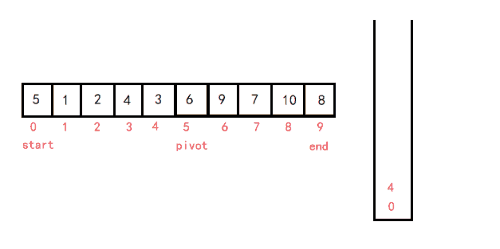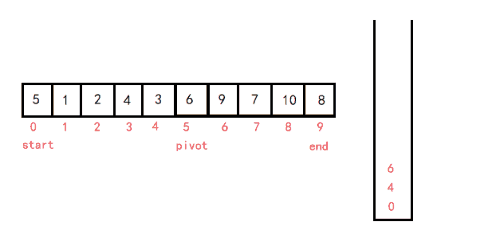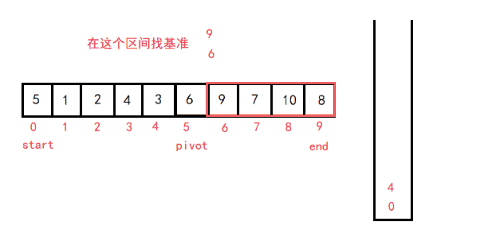
6. 快速排序（重要）
递归法：（挖坑法）
- 从待排序区间选择一个数，作为基准值(pivot)
- 遍历整个待排序区间，将 <= 基准值的放到基准值的左边，> 基准值的放到基准值的右边
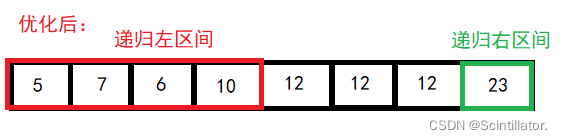
- 采用分治思想，对左右两个小区间 按照同样的方式处理，直到小区间的长度 <= 1
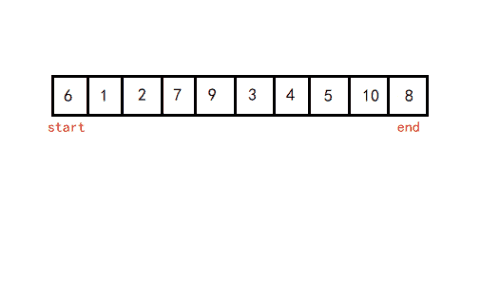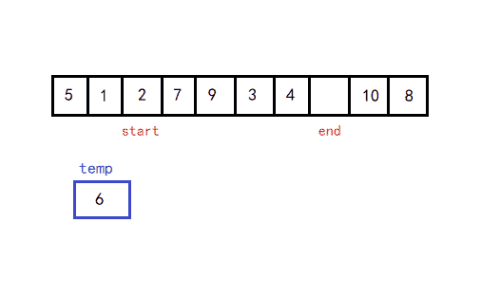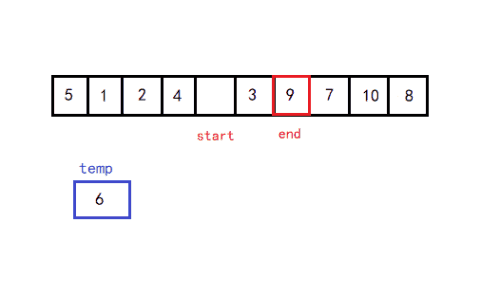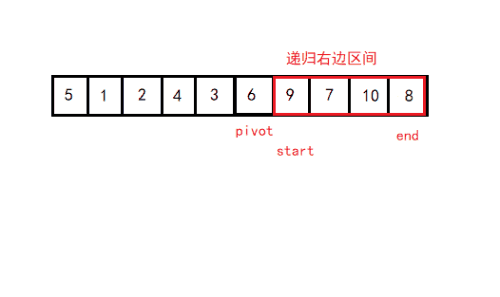
第一次排完序后，左边的数字都比基准值小，右边的数字都比基准值大。再递归基准位置的左边和右边。
/**
* 时间复杂度： O(N * logN)
* 空间复杂度： O(logN)
* 稳定性： 不稳定
*/
public void quick(int[] arr,int left,int right){
// 终止条件： left >= right ,不需要对该区间进行排序了,已经有序或者没有数据
if (left >= right) {
return;
}
// 找到基准，并将 <= 基准值的放到基准值的左边，> 基准值的放到基准值的右边
// 基准位置为 pivot
int pivot = partition(arr,left,right);
// 递归基准的左边子区间
quick(arr,left,pivot-1);
// 递归基准的右边子区间
quick(arr,pivot+1,right);
}
// 找基准
public int partition(int[] arr,int start,int end){
int temp = arr[start];
while (start < end){
while (start < end && arr[end] >= temp){
end--;
}
// end找到小于 temp的值，填补空格
arr[start] = arr[end];
while (start < end && arr[start] <= temp){
start++;
}
// start找到大于 temp的值，填补空格
arr[end] = arr[start];
}
// 将temp的值给最后的空格, 即基准位置
arr[start] = temp;
return start;
}
-
时间复杂度：
- 最好情况 O(N * logN)
- 最坏情况 O(N^2) （数据本来就有序）
-
空间复杂度：
- 最好情况 O( logN)
- 最坏情况 O(N) （数据本来就有序）-- 化为一颗单分枝树
-
稳定性： 不稳定
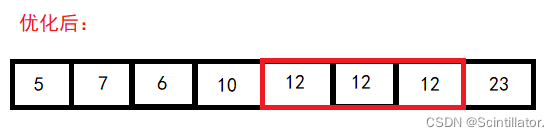
优化：
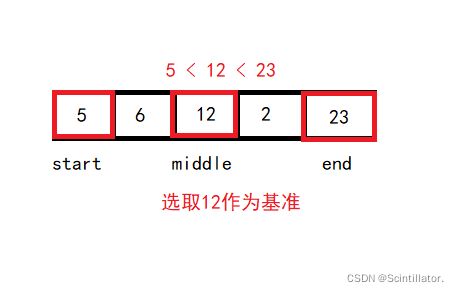
为了预防有序情况下，时间复杂度和空间复杂度太高，在找基准的时候，需要做出优化：
- 在可选区间内随机选取某个值作为基准 – 随机选取基准法
- 求得 start 和 end 下标的中间下标值，将三个值中大小位于中间的值作为基准值 — 三数取中法
// 找到三数的中间大小值
public int findMiddle(int[] arr,int start,int end){
int middle = start + ((end - start) >>> 1);
int max = Math.max(arr[start],Math.max(arr[middle],arr[end]));
int min = Math.min(arr[start],Math.min(arr[middle],arr[end]));
if(start != max && start != min){
return start;
}else if(middle != max && middle != min){
return middle;
}else {
return end;
}
}
- 将等于基准值的数和基准值放在一起
- 因为直接插入排序越有序越快，在区间比较小时，数据越趋于有序，用直接插入法排序
非递归法：（借助栈）
每弹两个数 — 找一次基准
/**
* 非递归实现快速排序
*/
public void quickNor(int[] arr){
Stack<Integer> stack = new Stack<>();
int left = 0;
int right = arr.length-1;
// 找到基准
int pivot = partition(arr,left,right);
// 左边区间至少有两个数，需要再排序
if (pivot - 1 > left){
// 放入左区间的左边边界点
stack.push(left);
// 放入左区间的右边边界点
stack.push(pivot-1);
}
// 右边区间至少有两个数，需要再排序
if (right - 1 > pivot){
// 放入右区间的左边边界点
stack.push(pivot+1);
// 放入右区间的右边边界点
stack.push(right);
}
while (!stack.isEmpty()){
// 弹出两个元素作为一个区间
right = stack.pop();
left = stack.pop();
// 找到基准
pivot = partition(arr,left,right);
// 左边区间至少有两个数，需要再排序
if (pivot - 1 > left){
// 放入左区间的左边边界点
stack.push(left);
// 放入左区间的右边边界点
stack.push(pivot-1);
}
// 右边区间至少有两个数，需要再排序
if (right - 1 > pivot){
// 放入右区间的左边边界点
stack.push(pivot+1);
// 放入右区间的右边边界点
stack.push(right);
}
}
}
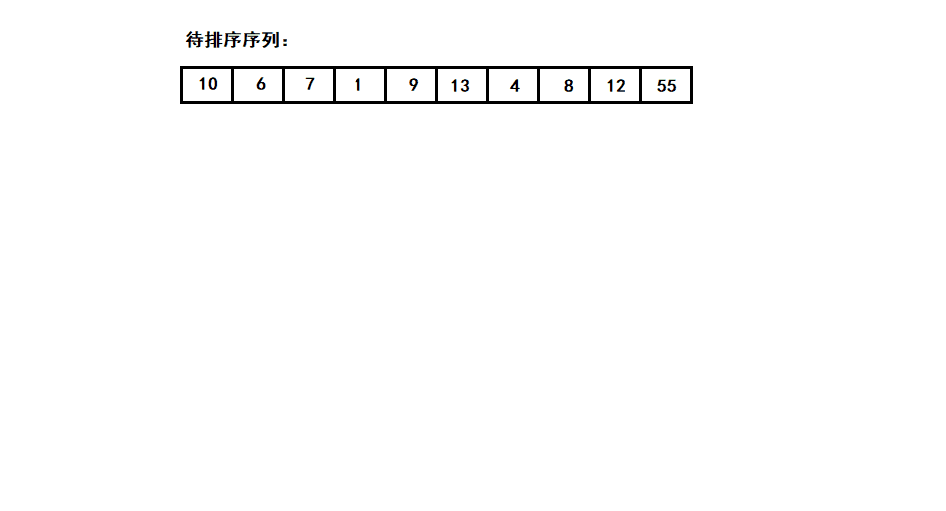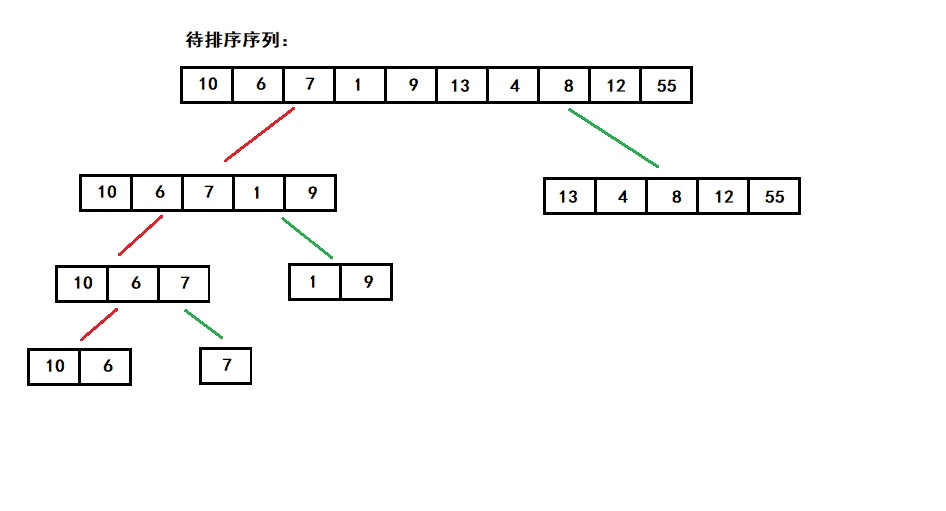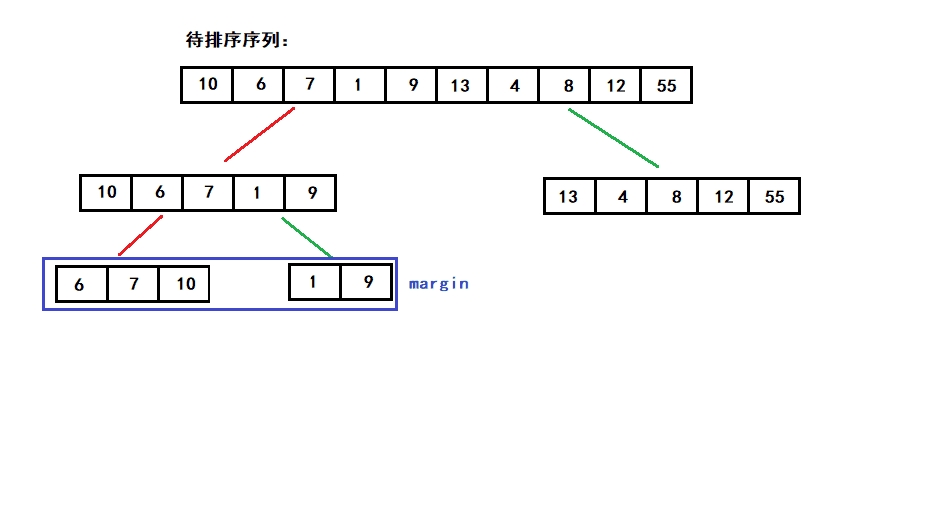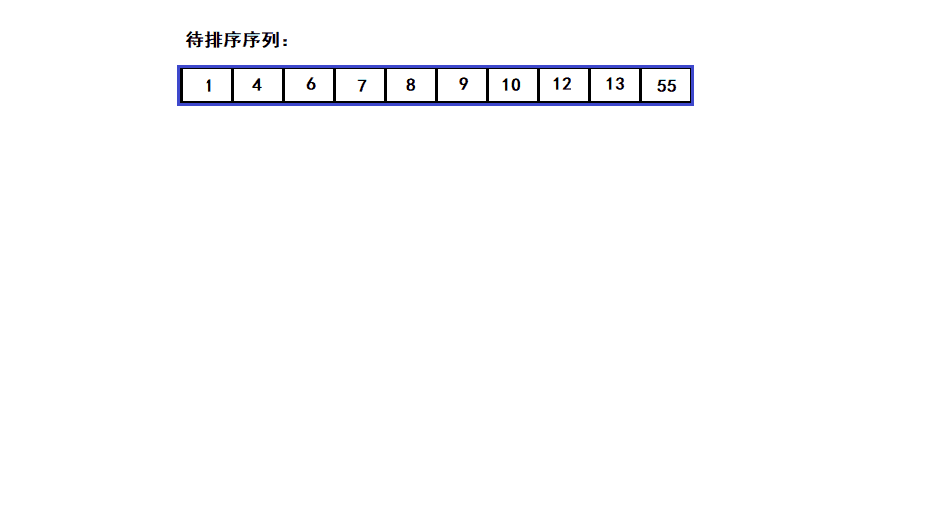
7. 归并排序（重要）
给你两个有序数组，合并为一个有序数组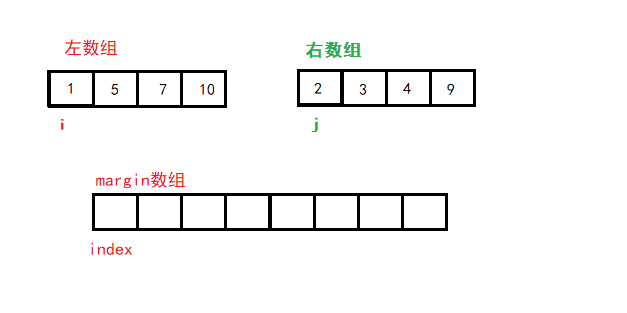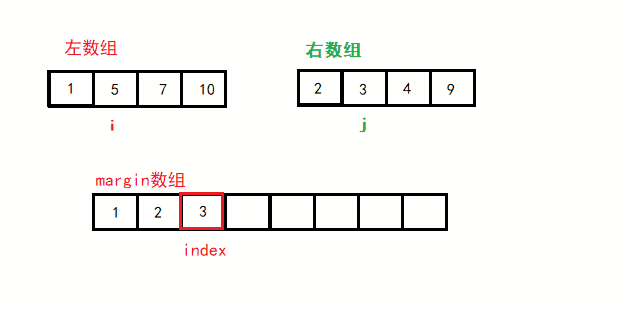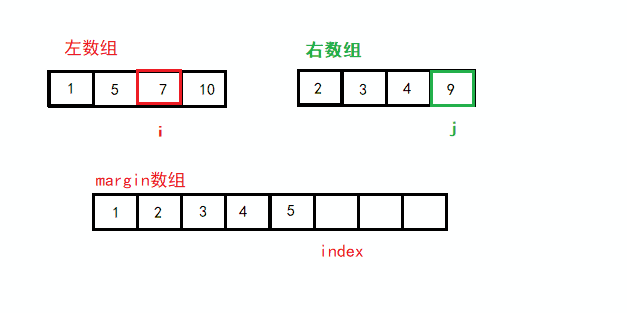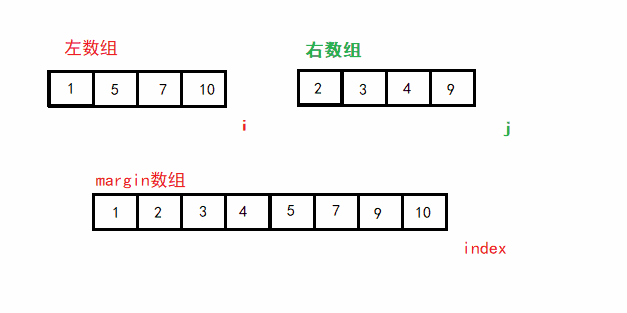
归并排序采用分治法， 将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。
即 先分解再合并（二路归并）
/**
* 归并排序
*/
public void mergeSort(int[] arr){
mergeSortInternal(arr,0,arr.length-1);
}
public void mergeSortInternal(int[] arr,int left,int right){
if (left >= right){
return;
}
int middle = (left + right) >>> 1;
// 递归左边
mergeSortInternal(arr,left,middle);
// 递归右边
mergeSortInternal(arr,middle+1,right);
// 归并
merge(arr,left,middle,right);
}
public void merge(int[] arr,int left,int middle,int right){
int s1 = left;
int e1 = middle;
int s2 = middle+1;
int e2 = right;
int[] temp = new int[right-left+1];
int index = 0;
while (s1 <= e1 || s2 <= e2){
if (s1 <= e1 && s2 <= e2){
if (arr[s1] <= arr[s2]){
temp[index++] = arr[s1++];
}else {
temp[index++] = arr[s2++];
}
}else if (s1 <= e1){
temp[index++] = arr[s1++];
}else {
temp[index++] = arr[s2++];
}
}
// 将 temp数组拷贝到 arr的 left~right区间
for (int i = 0; i < temp.length; i++) {
arr[i + left] = temp[i];
}
}
- 时间复杂度： O(N * logN)
- 空间复杂度：O(N)
- 稳定性： 稳定
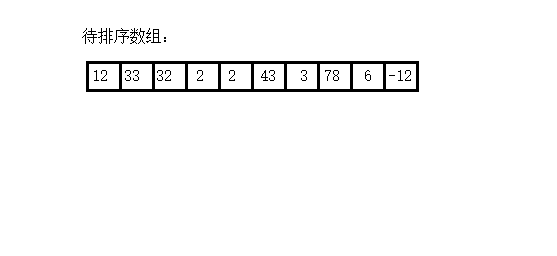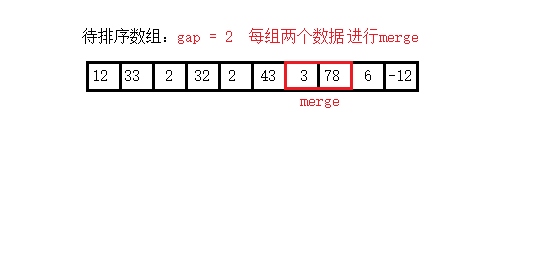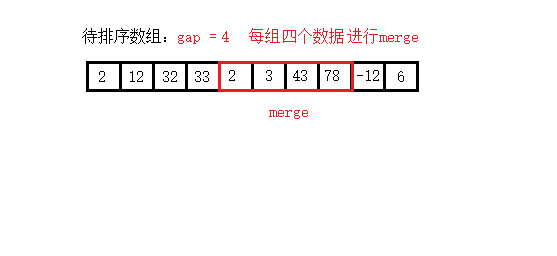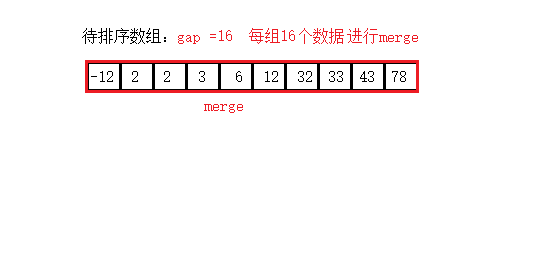
非递归实现归并排序： 2个数据归并 —> 4个数据归并 —>…—> 全部归并
public void mergeSortNor(int[] arr){
int gap = 2;// 初始每组两个数据
while (gap <= arr.length*2){
for (int left = 0; left < arr.length; left += gap) {
// 找到 right 的位置，处理越界
int right = (left + gap - 1 < arr.length) ? (left + gap - 1) : arr.length-1;
// 找到 middle 的位置，处理越界
int middle = (left + gap/2 - 1 < arr.length) ? (left + gap/2 - 1) : arr.length-1;
// 合并当前区间
merge(arr,left,middle,right);
}
gap *= 2;
}
}
总结
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 直接插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n^1.3) | O(n^1.5) | O(1) | 不稳定 | |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |