加油站问题-贪心算法（面试题JS）

        一辆汽车加满油后可行驶n公里。旅途中有若干个加油站。设计一个有效算法，指出应在哪些加油站停靠加油，使沿途加油次数最少。对于给定的n(n <= 5000)和k(k <= 1000)个加油站位置，编程计算最少加油次数。

　　要求：

　　输入：第一行有2个正整数n和k，表示汽车加满油后可行驶n公里，且旅途中有k个加油站。接下来的1 行中，有k+1 个整数，表示第k个加油站与第k-1 个加油站之间的距离。第0 个加油站表示出发地，汽车已加满油。第k+1 个加油站表示目的地。

　　输出：输出编程计算出的最少加油次数。如果无法到达目的地，则输出”NoSolution”。
 

贪心算法（又称贪婪算法），是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

贪心算法不是对所有的问题都能得到整体最优解，关键是贪心算法策略的选择。也就是说，不从整体最优上加以考虑，做出的知识在某种意义上的局部最优解。

对于加油站问题的解法来说，每次只走一小站，然后此处这两站之间的问题就是整体的问题的一个局部。到底怎样才能走到下一站呢？这是我们解决这个问题的关键，在一个加油站可以选择加油或者不加油，如若在每一个加油站都加油的话，在两个加油站之间的距离是加油后能走距离的最大距离，那肯定可以运动到最后一个加油站，但显而易见的是，这种想法肯定不是最优解，当我们在第k个加油站时，无论时候能走完k站与k+1站之间的距离都去选择加油，而实际上，当此时剩下的油量所能走过的路程大于k-k+1加油站距离时是可以选择不加油的，只有必须加油的时候才选择加油，这样才能最大限度的降低加油的次数，也就可以得到最少加油次数，即最优解。

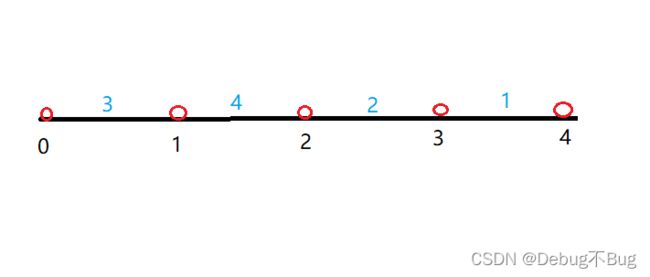
举个例子来说：（n=5,k=3,dis=[ 3,4,2,1 ]）

如图，红圈代表加油站，中间 3个加油站，现在需要从第0个加油站运动到第k+1个（即第4个）加油站的距离，dis数组用来存放加油站之间的间隔距离，count=0用来记录需要的最少加油次数，s=n用来代表此时的油量还可供走过多少的路程（初始状态为加满油，则初始赋值为加满油的最大距离n）。

k=0（初始状态）: s=n=5, count=0

        s > dis[0]=3（判断能否到下一个加油站，不能则无解）

        此时能，则 s=s-dis[0]=5-3=2;

k=1: s=2,n=5,count=0

        s < dis[1]=4 （判断能否到下一个加油站，能则不加油）

        此时不能，则加满油, s=n=5,count=count+1=1,

                s>dis[1]=4,则s =s-dis[1]=5-4=1,

k=2:s=1,n=5,count=1

        s < dis[2]=2 （判断能否到下一个加油站，能则不加油）

        此时不能，则加满油, s=n=5,count=count+1=2,

                s>dis[2]=2,则s =s-dis[2]=5-2=3,     

k=3:s=3,n=5,count=2

        s > dis[3]=1 （判断能否到下一个加油站，能则不加油）

        此时能,s =s-dis[3]=3-1=2,

最终,count=2,则最少加油次数为2.

附上个人代码：