给定加油站油量gas数组，去下一站所需的油耗数组cost，请问车辆从某一站出发能沿着环走一圈吗？

给定加油站油量gas数组，去下一站所需的油耗数组cost，请问车辆从某一站出发能沿着环走一圈吗？

提示：这个题是超超超难度的题目，笔试有笔试的方法，面试有面试的方法，核心在是否能优化出时间复杂度，同时尽量优化空间复杂度

---

题目

给定加油站油量gas数组，即加油站放好的油，你可以用
去下一站所需的油耗数组cost，从i位置去i+1位置，即下一站
请问车辆从某一站出发，只能逆时针走，能沿着环走一圈吗？能的话请范围起点（题目中的起点是唯一的）

---

一、审题

示例：比如：
gas=32241
cost=23212
黑色代表gas，加油站的油量，绿色代表cost，从i位置去i+1消耗的油耗
粉红色代表拿着本站的油，去下一站之后，油箱里还剩余多少油？rest数组 我们称之为纯能值数组
红色结果是rest又加上了加油站的油【中间值，不管】

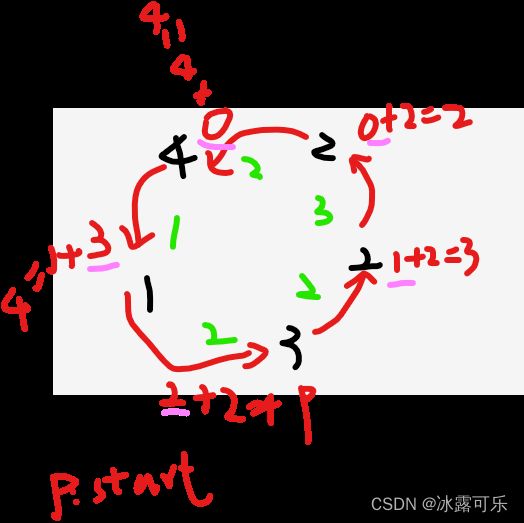
在这个过程中，纯能值数组rest的累加和sum，其瓶颈，意味着我到下一站的过程中，累加剩多少油，如果这个sum<0，你压根到不了下一站的。

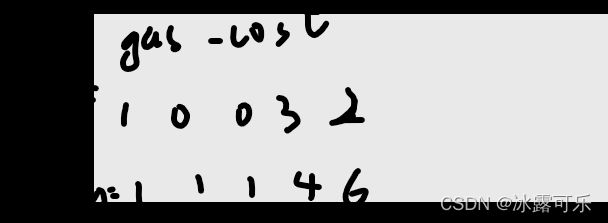
瓶颈就是累加剩油剩得最少的那段，其他地方剩得多，随意了
由于从i=0出发，整个过程中，sum的瓶颈均>=0，故从i=0出发，可以走一圈！
return 0；就行

本案例当然可以有别的起点，但是考题就1个。
我们要找的就是这个起点，否则返回-1；

---

二、解题：笔试用的方法0(n)空间复杂度，o(n)时间复杂度

看了案例大致也明白：

暴力解o(n^2)时间复杂度–不行的

我们最起码有一个暴力解o(n^2)时间复杂度
也就是判断每一个i位置，从i走一圈，然后看看瓶颈是否大于等于0，是就能，否则就不能
这样的话需要o(n^2)，笔试测试都过不了的。

//暴力方法是不行的，超出时间限制，都别想了就
        public int canCompleteCircuit1(int[] gas, int[] cost) {
            //暴力方法o(n^2)复杂度，o(n)额外空间消耗
            //从每个点出发，检查，它是否能走到底
            //简化一下，gas是加油站的油，cost是本站走到下一站，消耗的油，如果我还剩>=0单位的油，可以继续加下一站的油，到下下站
            //也就是gas-cost，从i出发时，我的累加剩余的油是不会低于0的，这就是我能到的出发点，返回结果就行

            int N = gas.length;
            int[] rest = new int[N];//o(n)额外空间
            for (int i = 0; i < N; i++) {
                rest[i] = gas[i] - cost[i];//剩余油
            }

            for (int i = 0; i < N; i++) {
                //枚举每一个i位置出发点
                int start = i;//出发点
                int sum = rest[start];//目前加了油走到下一站
                int j = nextIndex(start, N);
                for (; j != start; j = nextIndex(j, N)) {
                    //循环走回到start就停止
                    if (sum < 0) break;
                    sum += rest[j];//否则累加
                }
                if (sum >= 0) return i;//啥时候能走出一个sum>=0说明这个有效的
            }

            //一直没法让sum>=0
            return -1;
        }
        public static int nextIndex(int i, int N){
            return i == N - 1 ? 0 : i + 1;//越界就挪动到0，循环的下标
        }

笔试优化解：o(n)时间复杂度，o(n)空间复杂度

既然是想降低时间复杂度，就要牺牲空间了，由于笔试不对空间限制，故，可以牺牲空间复杂度，让时间AC即可
但是面试就尽量不要牺牲空间复杂度，因为实际公司没有那么多内存给你用。

咱们这样思考：能不能让i每次做一个开头，然后用o(1)速度把这个瓶颈拿出来判断一下？
也就是获取一个环，N长度的环，这个环内的最小值（纯能值），让这个纯能值保证>=0就可以走完一圈
N长度的环，在某个数组上的形式就是一个窗口，求窗口内的最小值？

——左神基础班讲过的单调栈寻找最值的
我们先把这个基础知识讲清楚：

如何找L–R窗内的最小值min，用单调栈来搞定

不妨设sum=35217，窗长N=3，让i从0开始往单调栈中放下标，比的时候比sum[i]的大小
整一个双端队列queue，保证左边小，右边大
（1）让i=0进来，意味着0位置的3可以进来
（2）i=1时，因为1位置的5大于queue的堆顶，OK，这满足单调性，1位置的5可以进去
（3）i=2，注意，此时来了一个2，显然你放2进去破坏了单调栈的单调性
此时堆顶value>新来的sum[i]，故，将堆顶弹出，1位置的5废了，同样0位置的3也得弹出，
栈空，放入2位置的2
注意：此时i=N-1=2，就是窗口已经形成了，3长度，准备收集答案，我们要的是最小值，自然就是堆低第一个值
也就是2位置的2是目前窗口内的最小值，没错吧？
（4）i=3,3位置的1，很小，比2小，弹出2位置的2，放入1
收答案，此时最小值是堆底的1，意味着窗口内的最小值就是1，没错吧？
（5）i=4，来了个7，7>1没错，满足单调性，让7进去，统计最小值
此时最小值依然是堆底的1，意味着窗口内最小值就是1，没错吧？
over
注意：每次要保证queue的尺寸size<=3,=N，当超过这个值，说明窗长太大，要弹出堆底那个值，保证L往右滑动，L–R恰好形成N长度的窗口。

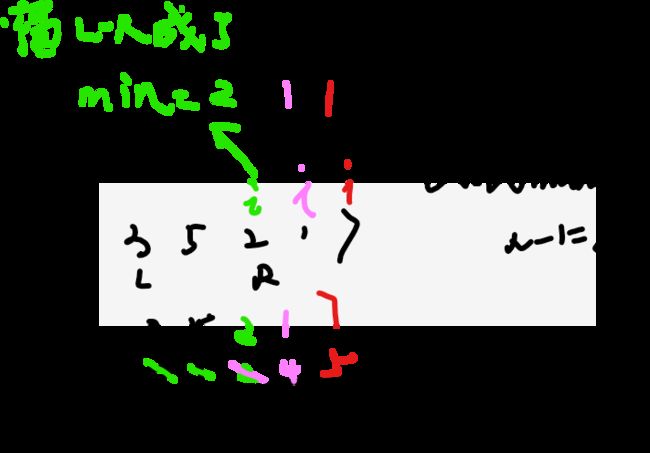
这样的话，每次走到sum的i位置，咱就可以轻松拿下整个窗口内的最小值min。o(1)

有了o(1)获取窗口L–R内的最值这种办法，那就可以解决咱们现在这个问题了
下面我们看看如何将L–R这窗口模拟出来，
而且要每次都方便把i开头走一圈的纯能值数组rest求出来，还得快速拿到这rest的瓶颈。

我们需要额外的空间，造一个循环纯能值累加数组出来，每次求L–R范围内的纯能值瓶颈时
把L–R内的累加和瓶颈值summin-sum[L-1],这个就是纯能值的瓶颈

看图：
gas=32241
cost=23212
则纯能值数组为：
rest=gas-cost=1 -1 0 3 -1
这个数组当然是i=0为出发点，走一圈，所剩的油量，我们还需要看别的i位置出发的呢
不妨设i=1出发的话，走一圈从N-1绕回来到1才能算走完

我们把rest放成2排，造一个数组sum，让sum是rest的累加和，然后把rest再累加一遍，就是sum为2N长度
从L–R的一个窗口：
（1）当L=0时，从i=0出发走一圈的纯能值数组累加和就是sum，看瓶颈min，如果min=0>=0则说明从i=0位置出发能走一圈
（2）当L>=1时，你sum[L-1]代表你把0–L-1都累加进来了，我们现在只要L–R，那就需要你把多加入的0–L-1减掉即：
sum[i]-sum[L-1]
把pre定义为sum[L-1]，则sum[i]-pre就是L–R内的真实的纯能值累加和，找这个瓶颈min
比如i=1吧，sum那0位置就是多累加的：sum[i]-sum[L-1]
需要把00323减掉1
即：-1-1212
现在干脆你直接从1位置累加呢？
得：-1-1212
是不是与sum[i]-sum[L-1]一样呢？当然是一样的
这就是为啥我们要单独拿2次rest累加为sum的原因，这样的话，我们在求任意L–R的纯能值累加和瓶颈时，只需要找一个min，然后再减pre。就这么容易

然后就优化出来了
看代码，代码是非常精简的，这个L–R上的窗长不妨设N长度
（1）最开始i=0开始，我们R开始扩，一旦i-（N-1）>=0了，说明N长的窗口已经形成，可以收答案了

此时就分：
（2）i=N-1代表，L=0，第一个窗开始走，sum的瓶颈不用减谁
（3）当i>N-1，说明L>=1，后面的窗口，sum的瓶颈都需要减sum[i-(N-1)-1]=sum[i-N]
因为此时窗口的L=i-(N-1)=i-N+1
看这个瓶颈>=0吗，是就返回L
如果所有的环都不行，那返回-1

//本题，笔试与面试均可以AC方法
        //拼燃油差数组，然后用窗口内瓶颈判断这个位置是否能作为合适的出发点？
        //因为你是走一圈，所以需要i--N-1每个点作为触发点，走一圈，每个瓶颈保证累加过程中燃油差的累加和>=0
        //燃油差offset = gas - cost
        //这个差数组，在任意一个i位置出发，如果累加和>=0就可以继续往下走，所以弄一个燃油差累加和出来，再去判断，一个圈内的瓶颈就行
        public static int canCompleteCircuit(int[] gas, int[] cost){
            int N = gas.length;
            int[] offset = new int[N];
            for (int i = 0; i < N; i++) {
                offset[i] = gas[i] - cost[i];
            }

            int[] sum = new int[N << 1];
            //第一圈
            int index = 0;
            sum[index++] = offset[0];
            for (int i = 1; i < N; i++) {
                sum[index] = sum[index - 1] + offset[i];//累加
                index++;
            }
            //第2圈
            sum[index] = sum[index - 1] + offset[0];
            index++;
            for (int i = 1; i < N; i++) {
                sum[index] = sum[index - 1] + offset[i];//累加
                index++;
            }

            //得到了双拼的累加油差数组sum之后，开始从i==0--N-1判断，以N长度为窗口，找瓶颈最小值
            //这个瓶颈，就是在走一圈累加过程中最瓶颈的地方，如果它>=0，没问题
            //注意，首次i==0出发时，累加和瓶颈就是自己
            //但是i==1开始，注意累加和已经算上了i==0的点，需要把i-1之前的油量减掉

            LinkedList<Integer> queue = new LinkedList();
            for (int i = 0; i < 2 * N; i++) {
                //每次一个N代表能走一圈
                //一个双端队列，左边放小的数，一旦i比尾部小，直接弹出尾部，保证左边头小
                while(!queue.isEmpty() && sum[queue.peekLast()] >= sum[i]) queue.pollLast();

                queue.addLast(i);//记录位置，每次都需要，但是保证左边都得比我小才行

                //窗口到N就过期，同时收集答案
                if (queue.peekFirst() == i - N) queue.pollFirst();
                if (i >= N - 1){
                 //形成了一个窗口
                    if (i == N - 1){//当窗口左边为0时，说明第一个窗
                        if (sum[queue.peekFirst()] >= 0) return 0;
                    }
                    else {//不是第一个窗口，就看瓶颈了
                        int min = sum[queue.peekFirst()] - sum[i - N];//减掉前面累加油量的瓶颈
                        if (min >= 0) return i - N + 1;//返回的是那个窗口的第一个位置---训练coding能力
                    }
                    //否则就要把之前的油量减掉
                }
            }

            return -1;//全部看完，一个都不行的话，废
        }
        //当然，左神做了更通用的，请范围每一个位置i是否合法，那就不要return就行，每次都进行收集ans就可以，easy

解释一下：

 if (queue.peekFirst() == i - N) queue.pollFirst();

这句代码就是在控制queue的长度size必须为N，每次都要弹出第一个栈底，否则就说明窗口太大，你得让L++，上面基础知识那讲清楚了。

测试代码：

 public static void test(){
//        int[] gas  = {2,3,4};
//        int[] cost = {3,4,3};
        int[] gas  = {1,2,3,4,5};
        int[] cost = {3,4,5,1,2};
        //这个是不行的
        Solution solution = new Solution();
        System.out.println(solution.canCompleteCircuit1(gas, cost));//可以做对数器用
        System.out.println(solution.canCompleteCircuit(gas, cost));//可以做对数器用

    }

    public static void main(String[] args) {
        test();
    }

三、面试用的方法：0(1)空间复杂度，o(n)时间复杂度

整个方法极其复杂，千万别在笔试的时候写，只能在面试场上给面试官秀一下
即使是面试，也要先用笔试的方法先给面试官讲清楚，然后再秀这个方法

整个最优解的核心思想是：
想办法接通首尾区间[start,end)，剩油扩尾，不行扩头
start是包含start这个点，end不包含哦

首先我们来讲如何省空间，让cost来存rest，这样就不要外部空间了，反正我们的gas和cost也就用一次而已，看下图

好，有了cost，cost就是rest数组
我们来模拟整个剩油就扩尾，不行就扩头的算法大流程：
这里有四个重要的变量：[start,end)代表车能从start走到end，不含end点，start是联通区的头，end是联通区的尾。
rest，目前连通区域内车所剩的油量，有剩余则可以扩尾部，去下一个点；
need，目前要来到start位置，想接上联通区域，所需要的油量，耗了这么多油才能到start与联通区域接上。

（1）任选一个cost[i]>=0的点i，既然cost[i]>=0说明从这个点可以作为start点，先令end=i+1,【[start,end) 代表车子可以走通的区域】
能否去下一个点呢?
那得看一个变量rest，即整个start–end上所剩的整体油量，rest它是否>=0？
——如果是，代表剩油，可以扩尾部end：
end++，rest+=cost[end],继续看rest能否增加？

然后遵循的原则就是：剩油扩尾，不行扩头

——那如果此时rest<0了，自然end无法++了，这说明，现在的start为起点，走一圈那是行行不通的。

考虑去扩头吧，那就要一个新的变量了：need，车辆从start-1点，想要来到start点所需的油量
（2）现在你start-1想接上[start,end)联通区，就要need这么多油，你cost[start-1]够吗？
——如果cost[start-1]>=need,可以直接让start变start-1,然后把rest更新一下：rest+=o[start]-need;把刚刚接上了消耗那点油给减掉
然后回到（1）；
——如果cost[start-1]<0呢？显然没法接，不好意思，rest也不可能有剩油，那此时start是无法出发走一圈了
那么想要start-1接上[start,end)联通区，那得要求你need-=cost[start-1]，你负，需要变正，就得需要这么多油才能接；

然后继续遵循：剩油扩尾，不行扩头

说个案例,咱就能理解整个算法流程了
第一个：失败的案例，永远没有一个点可以搞定：
cost【此时已经被我们认为是rest数组了（笔试题中那个rest数组）】
cost=7 -3 -4 -5 3 -7 -2 6 -2
a b c d e f g h i

寻找一个cost>=0的点，不妨设start为a，则
现在，start=a点，end=b点，[a,b)代表目前两痛了a–a，因为不含b
rest=cost[a]=7;从a出发，目前车省了这么多油
need=0;只需要0油就能自然来a点

开始模拟：剩油就扩尾，没油就扩头
（1）rest=7>=0，因为rest+=cost[end]=7-3=4>=0,故end++，end=c；同时让need清零；
（2）rest=4>=0，因为rest+=cost[end]=4-4=0>=0,故end++，end=d；同时让need清零；
（2）rest=0>=0，因为rest+=cost[end]=0-5=-5<0,故没法扩尾部了，没油就扩头——也宣告start=a出发无法走一圈了
判断cost[start-1]=cost[i]=-2 现在，咱们需要让start-1接到start上，则需要的油为：need-=cost[start-1]=0-（-2）=2,start=start-1=i;
（3）看start-1=h处cost[h]=6>=need=2，则说明，h出发，可以有油走到i来，start=h
则rest=cost[h]-need=6-2=4,既然有剩油了，那将need清零；
（4）rest=4>=0,可以考虑扩尾了，因为rest+=cost[end]=4-5=-1<0，故没法扩尾，没油就扩头，——也宣告start=h出发无法走一圈了
（5） 判断cost[start-1]=cost[g]=-2 现在，咱们需要让start-1=g接到start=h上，则需要的油为：need-=cost[start-1]=0-（-2）=2,start=start-1=g;
（6）判断cost[start-1]=cost[f]=-7 现在，咱们需要让start-1=f接到start=g上，则需要的油为：need-=cost[start-1]=2-（-7）=9,start=start-1=f;
（7）判断cost[start-1]=cost[e]=3 现在，咱们需要让start-1=e接到start=f上，则需要的油为：need-=cost[start-1]=9-（3）=6,start=start-1=e;
（8）判断cost[start-1]=cost[d]=-5 现在，咱们需要让start-1=d接到start=e上，则需要的油为：need-=cost[start-1]=6-（-5）=11,start=start-1=d;
此时，start都到end了，一个接不上，真个环都不行

第二个：成功的案例：
cost【此时已经被我们认为是rest数组了（笔试题中那个rest数组）】
cost=3 -2 -4 2 -1 -3 4 6 -1
a b c d e f g h i

寻找一个cost>=0的点，不妨设start为a，则
现在，start=a点，end=b点，[a,b)代表目前两痛了a–a，因为不含b
rest=cost[a]=3;从a出发，目前车剩了这么多油
need=0;只需要0油就能自然来a点

开始模拟：剩油就扩尾，没油就扩头
（1）rest=3>=0，扩尾，因为rest+=cost[end]=3-2=1>=0,故end++，end=c；同时让need清零；
（2）rest=1>=0，扩尾，因为rest+=cost[end]=1-4=-3<0,故end没法扩了——宣告此时start=a的出发点走一圈失败了
判断cost[start-1]=cost[i]=-1 现在，咱们需要让start-1接到start上，则需要的油为：need-=cost[start-1]=0-（-1）=1,start=start-1=i;
（3）判断cost[start-1]=cost[h]=6>=need=1,故可以自由链接，start=h，还剩rest+=cost[h]-need=1+6-1=1+5=6这么多油【之前rest=1原来剩一点】，既然rest有剩余那就要往尾扩，此时need清零；
（4）rest=6>=0，扩尾，因为rest+=cost[end]=6-4=2>=0,故end++，end=d；同时让need清零；
（5）rest=2>=0，扩尾，因为rest+=cost[end]=2+2=4>=0,故end++，end=e；同时让need清零；
（6）rest=4>=0，扩尾，因为rest+=cost[end]=4-1=3>=0,故end++，end=f；同时让need清零；
（7）rest=3>=0，扩尾，因为rest+=cost[end]=3-3=0>=0,故end++，end=g；同时让need清零；
（7）rest=0>=0，扩尾，因为rest+=cost[end]=0+4=4>=0,故end++，end=h；同时让need清零；
此时end=h=start了，故接上了整个区域，证明整个h出发车能够走一圈。

到此，两个案例，是不是已经明了：剩油就扩尾，不行就扩头
写代码这里是非常考研人的技术的，coding清楚整个思想，就成功了。
【下午我写写试试看，成功了，可以的】仔细研读代码，理解上面这个核心思想，这是面试的王牌

//左神还有一个办法：
        //o(1)额外空间，o(n)复杂度，用有限几个变量搞定，利用联通区收拾，面试可以讲给面试官听
        //难的，尽力去听，一定要拿下，因为面试非常高频问的难题，每年都可能会出现的题

        //面试的代码核心思想为：剩油扩尾，没油扩头
        //俩rest和need变量监控这一切行为：

        public int canCompleteCircuitFace(int[] gas, int[] cost){
            int N = gas.length;
            //cost 替代rest
            int start = -1;
            for (int i = 0; i < N; i++) {
                cost[i] = gas[i] - cost[i];
                //找到一个位置costi>=0即从这个开始寻
                if (start == -1 && cost[i] >=0) start = i;
            }

            //然后设定end
            int end = nextIndex(start, N);
            int rest = cost[start];//最初剩余油量
            int need = 0;//最初只需0就就能到联通区域[start,end)

            while (start != end){
                //没接上的话，就继续扩，不管扩头还是扩尾

                //只要剩油就扩尾，rest>=0就可以扩尾
                int nextRest = rest + cost[nextIndex(end, N)];//看看能扩吗
                while (start != end && nextRest >= 0){
                    //确实可以扩尾
                    rest = nextRest;
                    end = nextIndex(end, N);//扩
                    need = 0;//让need清零

                    nextRest = rest + cost[nextIndex(end, N)];//看看能扩吗
                }
                //一旦不能扩了，rest就先攒着

                //没油就扩头
                //当然首先要保证start!=end
                if (start != end){
                    if (cost[lastIndex(start, N)] < need){
                        //不够，来不了，那需要多少，填上这么多油，才能来start
                        need -= cost[lastIndex(start, N)];
                    }else {
                        //cost[lastIndex(start, N)] >= need
                        //说明可以直接过来，说不定还剩油呢，而且又可以去扩尾了
                        rest += cost[lastIndex(start, N)] - need;//消耗了need，来到start，把剩余的油加上
                    }
                    //不管头能否链接，start都得去前面了，尾不能扩，说明刚刚start出发无法走一圈了
                    start = lastIndex(start, N);//扩头链接[start,end)
                    //然后回到
                }
            }


            return need >= 0 ? start : -1;//全部看完，一个都不行的话，废
        }

---

总结

提示：重要经验：

1）笔试题：由于笔试不对空间限制，故，可以牺牲空间复杂度，让时间AC即可；
2）笔试那个代码一定要搞清楚，已经很牛逼了
3）单调栈，找窗口内的最大值或者最小值，思想非常厉害，理解整个思想，搞懂整个代码，然后才能改变出这个题的解法。
4）笔试就写笔试那套代码，保险，面试时，先写笔试那套，再秀这个面试的思想，非常优秀的！！！！