【论文阅读】DiffusionDet: Diffusion Model for Object Detection
原文链接:https://arxiv.org/abs/2211.09788
1. 引言
过去的目标检测方法依赖手工设计的候选对象(如滑动窗口、区域提案、锚框和参考点);或是依赖可学习的物体查询。
本文使用更加简单的方法,随机初始化边界框(不含可学习参数或启发式先验),直接从噪声框中细化位置和尺寸。这种从噪声生成边界框的方法与去噪扩散模型生成图像的过程类似。
DiffusionDet将目标检测任务视为边界框中心和尺寸的生成任务。在训练阶段,高斯噪声会添加到真实边界框中,得到带噪声的边界框;然后带噪声的边界框会用于裁剪RoI内的、图像编码器输出的特征,进一步输入检测头进行边界框预测。推断阶段,DiffusionDet通过将噪声先验分布调整为学习到的分布,来生成边界框。
DiffusionDet可以训练一次就用到不同的推断设置中。例如,推断时使用的随机边界框数量不需要和训练时相同;推断时可任意调整去噪采样步数来平衡性能与推断时间。
3. 方法
3.1 准备知识
目标检测的任务是从图像 x x x估计边界框集合 b ∈ R N × 4 b\in\mathbb{R}^{N\times4} b∈RN×4和类别标签 c c c。
扩散模型通过对样本数据逐步添加噪声,定义了前向扩散过程的一个马尔科夫链。前向过程如下: q ( z t ∣ z 0 ) = N ( z t ∣ α ˉ t z 0 , ( 1 − α ˉ t ) I ) , t ∈ { 1 , 2 , ⋯ , T } q(z_t|z_0)=\mathcal{N}(z_t|\sqrt{\bar{\alpha}_t}z_0,(1-\bar{\alpha}_t)I),t\in\{1,2,\cdots,T\} q(zt∣z0)=N(zt∣αˉtz0,(1−αˉt)I),t∈{1,2,⋯,T}其中 α ˉ t : = ∏ s = 0 t α s = ∏ s = 0 t ( 1 − β s ) \bar{\alpha}_t:=\prod_{s=0}^t\alpha_s=\prod_{s=0}^t(1-\beta_s) αˉt:=∏s=0tαs=∏s=0t(1−βs), β s \beta_s βs表示噪声方差。神经网络 f θ ( z t , t ) f_\theta(z_t,t) fθ(zt,t)会通过最小化如下的训练目标,从 z t z_t zt预测 z 0 z_0 z0: L train = 1 2 ∥ f θ ( z t , t ) − z 0 ∥ 2 \mathcal{L}_\text{train}=\frac{1}{2}\|f_\theta(z_t,t)-z_0\|^2 Ltrain=21∥fθ(zt,t)−z0∥2 推断时,数据样本 x 0 x_0 x0会使用模型 f θ f_\theta fθ从噪声样本 z T z_T zT迭代地重建。
本文的数据样本为 z 0 = b z_0=b z0=b。给定条件 x x x,神经网络 f θ ( z t , t , x ) f_\theta(z_t,t,x) fθ(zt,t,x)会从带噪声的边界框 z t z_t zt预测 z 0 z_0 z0,并相应生成类别标签 c c c。
3.2 结构
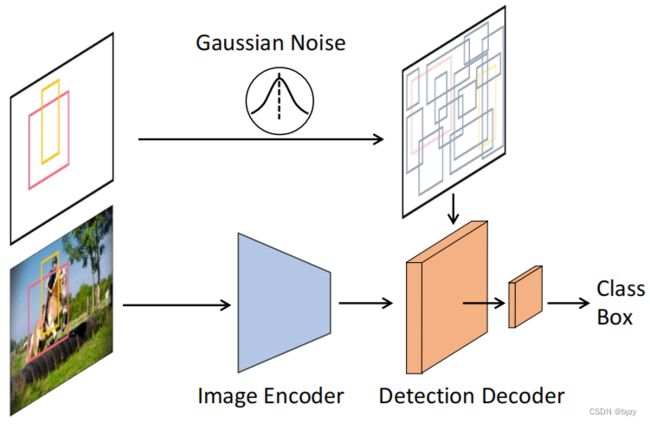
在每个迭代步骤直接将 f θ f_\theta fθ应用于原始图像在计算量上是不可接受的。本文将整个模型分为两部分:图像编码器和检测解码器。前者只会运行一次,以得到输入图像的深度特征表达,后者将深度特征作为条件,逐步细化带噪声边界框 z t z_t zt。
图像编码器提取图像特征,包含CNN/Transformer主干+FPN。
检测解码器输入提案框的集合,从图像特征裁剪得到RoI特征,并输入检测头获取回归和分类结果。解码器与Sparse-CNN结构类似,使用6个级联阶段。区别在于本文使用随机边界框而非学习到的边界框,且无需提案特征。此外,DiffusionDet会在迭代采样阶段重复利用检测头,每个阶段会加入步数编码。
3.3 训练
训练算法如下:
- 图像编码器提取图像特征;
- 填充和缩放真实边界框得到 z 0 z_0 z0;
- 从 { 1 , 2 , ⋯ , T } \{1,2,\cdots,T\} {1,2,⋯,T}内均匀采样时间 t t t,从标准正态分布中采样噪声 ϵ \epsilon ϵ。计算 z t = α ˉ t z 0 + 1 − α ˉ t ϵ z_t=\sqrt{\bar{\alpha}_t}z_0+\sqrt{1-\bar{\alpha}_t}\epsilon zt=αˉtz0+1−αˉtϵ;
- 将图像特征、 z t z_t zt与 t t t输入解码器得到预测边界框;
- 计算预测边界框与真实边界框的损失。
真实边界框填充:通常不同图像中的实例数不同。本文通过向真实边界框集合中添加(填充)额外边界框,使得边界框总数为固定值 N train N_\text{train} Ntrain。填充方法包括重复已有边界框、添加随机边界框或添加图像大小的边界框。实验表明添加随机边界框的效果最好。
边界框破坏:向填充后的边界框集合添加噪声,噪声尺度由 α t \alpha_t αt控制。 α t \alpha_t αt服从单调递减余弦调度。此外,真实边界框需要缩放以保证信噪比。
训练损失:检测头输入 N train N_\text{train} Ntrain个被破坏的边界框,预测 N train N_\text{train} Ntrain个类别和候选框。使用集合预测损失,并按照最优传输分配方法,通过选择代价最小的 k k k个预测,为每个真实边界框分配多个预测。
3.4 推断
推断过程从采样自高斯噪声的边界框集合逐步细化为预测结果,算法如下所示。
- 图像编码器提取图像特征;
- 从标准正态分布中采样边界框提案 z T z_T zT;
- 从 t = T t=T t=T开始,进行下面的过程直到 t = 0 t=0 t=0:
将图像特征、 z t z_t zt与 t t t输入解码器得到预测边界框;
根据 z t z_t zt、预测边界框、 t t t与 t − Δ t-\Delta t−Δ,使用DDIM预测上一步的边界框提案 z t − Δ z_{t-\Delta} zt−Δ;(DDIM是一种采样时可跳步的扩散模型)
更新边界框提案 z t − Δ z_{t-\Delta} zt−Δ。
采样过程:将每一步得到的边界框提案输入解码器得到预测边界框后,使用DDIM估计上一步的边界框提案。去掉DDIM后,性能会有严重下降。
边界框更新:每一步采样后,预测的边界框可分为期望的预测(位于相应目标处)和不期望的预测(随意分布)。对于不期望的预测,其分布没有被学习,因此会被替换为新的随机边界框(从高斯分布中采样)。实际中,将分数低于特定阈值的预测视为不期望的预测。
一次训练适用于多种测试设置:由于随机边界框的设计,推断阶段采用的随机边界框数和采样阶段数无需和训练阶段保持一致。
4. 实验
4.1 实施细节
测试细节:每个采样步骤的预测结果会集成起来通过NMS,以获得最终的预测。
4.2 主要特性
DeffusionDet的主要特性为“一次训练适用于多种测试设置”。因此,可根据需要调整边界框数量和采样步数,以平衡速度和精度。
动态边界框:将DiffusionDet与DETR比较,固定训练时的边界框或物体查询数量 N train N_\text{train} Ntrain,改变测试时的边界框或物体查询数量 N eval N_\text{eval} Neval。对于DETR,由于测试时的查询数必须等于训练时的数量,因此当 N eval < N train N_\text{eval}
若DETR在 N eval > N train N_\text{eval}>N_\text{train} Neval>Ntrain使用复制已有查询的方法,性能下降会更严重。这是因为随机加入查询能提高查询的多样性。
逐步细化:固定随机边界框的数量,增加细化步数,性能仍有稳定提升;且随机边界框越少,增加细化步数带来的提升越大。
对于其余方法而言,仅可使用一次检测头,重复使用会导致性能下降(见附录)。
4.3 检测数据集上的性能分析
MS-COCO:不进行细化的时候,DiffusionDet已经能超过一些完善方法的性能。进行细化会进一步拉开差距。
当使用更大的主干网络时,DiffusionDet也能带来稳定的性能提升。
LIVS v1.0:与MS-COCO相比,DiffusionDet的细化在LIVS上的性能提升更加显著。这说明在更具挑战性的基准上,细化策略更有效。
4.4 消融研究
信号缩放:信号缩放因数控制扩散过程的信噪比。与图像生成和全景分割相比,本文使用的缩放因数更大,这是因为边界框的表达相比密集表达更加“脆弱”,更高的信噪比使其更容易训练。
GT边界框填充策略:实验表明,填充服从高斯分布的随机边界框比起其余填充方法(复制已有边界框、填充图像大小边界框、填充服从均匀分布的随机边界框)性能更优。
采样策略:不使用DDIM和边界框更新的情况下,性能会随步数增加而下降;使用其中之一时,仅会在有限的步数内略微提升性能,但更多步数不能带来性能提升。当同时使用两者时性能最优。
N train N_\text{train} Ntrain和 N eval N_\text{eval} Neval之间的匹配:无论 N train N_\text{train} Ntrain为多少,当 N eval N_\text{eval} Neval增加时,性能均能稳定提升;此外,固定 N eval N_\text{eval} Neval的情况下,当 N train N_\text{train} Ntrain和 N eval N_\text{eval} Neval匹配时性能最优。
精度vs.速度:设置 N train = N eval N_\text{train}=N_\text{eval} Ntrain=Neval进行测试,发现当 N train N_\text{train} Ntrain增加时能以微小的速度下降换取大幅性能提升。增加步数时,性能有一定提升,但速度下降明显。在相同提案数的情况下,DiffusionDet的速度与Sparse-CNN接近。
随机种子:使用不同的随机种子进行实验,DiffusionDet的性能稳定。
附录
A. 扩散模型的表达
相关介绍见扩散模型(Diffusion Model)简介(注意符号与本文有所不同)。
除了可使用网络 f θ ( z t , t ) f_\theta(z_t,t) fθ(zt,t)直接预测 ϵ \epsilon ϵ外,也可预测 z 0 z_0 z0。本文选择预测 z 0 z_0 z0。
B. 动态边界框
实验表明,Sparse R-CNN与Deformable DETR均不能在固定 N train N_\text{train} Ntrain的情况下随意改变 N eval N_\text{eval} Neval。这证明了DiffusionDet独特的动态特性。
C. 逐步细化
DETR、Sparse R-CNN、Deformable DETR在进行逐步细化时均会带来性能下降;当从各步整合预测结果时,Sparse R-CNN和Deformable DETR能减轻性能下降。但对于DiffusionDet,不进行整合时,性能下降可忽略;进行整合会带来性能提升。
E. 训练损失
集合预测损失被用于 N train N_\text{train} Ntrain个预测上。集合预测损失要求预测和真值之间逐对的匹配代价(同时考虑类别与边界框): C = λ c l s C c l s + λ L 1 C L 1 + λ g i o u C g i o u \mathcal{C}=\lambda_{cls}\mathcal{C}_{cls}+\lambda_{L1}\mathcal{C}_{L1}+\lambda_{giou}\mathcal{C}_{giou} C=λclsCcls+λL1CL1+λgiouCgiou其中 C c l s \mathcal{C}_{cls} Ccls为分类的focal损失, C L 1 \mathcal{C}_{L1} CL1和 C g i o u \mathcal{C}_{giou} Cgiou分别为边界框预测的L1损失和GIoU损失。
本文使用最优传输方法,为每个真值匹配多个预测结果。即选择代价最小的 k k k个预测作为某真值的正样本,其余为负样本。损失函数与前面的代价表达式相同,但仅在匹配对之间计算。