Shuffle Attetion

Abstract

广泛应用的注意力机制主要有空间注意力机制和通道注意力机制，其目的分别是捕捉像素级的成对关系和通道依赖关系。虽然将两种机制融合在一起可以获得比单独更好的性能，但计算开销不可避免。因而，本文提出Shuffle Attetion，即SA，以解决这个问题。SA采用Shuffle Units有效地结合两种注意力机制。具体来说，SA首先将通道维度分组为多个子特征，然后并行处理。对于每个子特征，SA利用Shuffle Units描述空间和通道维度上的特征依赖关系，然后对所有子特征进行聚合，采用channel shuffle算子实现不同子特征间的信息通信。

1. Introduction

1.1 背景

注意力机制分为两种，通道注意和空间注意，都是通过不同的聚集策略、转换和强化函数，从所有位置聚集相同的特征来增强原始特征。
GCNet和CBAM将通道注意和空间注意整合到一个模块中，在取得显著结果的同时，也存在存在收敛困难或计算负担过重的问题。
ECA-Net通过使用一维卷积简化了SE模块中信道权重的计算过程；SGE将通道的维度划分为多个子特征表示不同的语义，使用注意掩码在所有位置缩放特征向量，对每个特征组应用空间机制。然而这些网络没有充分利用空间注意和通道注意之间的相关性，致使其效率较低。

1.2 启发

ShuffleNet v2构建多分支结构，并行处理分支。具体来说，在这个unit开始时，$c$个特征通道的输入被分成两个分支，分别是$c-c^{\prime }$和$c^{\prime }$通道。然后，采用几个卷积层捕获输入的更高级表示。在卷积之后，将两个分支连接起来，使通道的数量与输入的数量相同。最后采用channel shuffle算子实现两个分支之间的信息通信。
SGE引入了分组策略，将输入特征映射沿通道维度划分为组，然后所有子特征可以并行增强，以提高计算速度。

1.3 提出

本文提出Shuffle Attention 模块，即SA。该模块按通道维度分组为子特征。对于每个子特征，SA采用Shuffle Unit同时构建通道注意和空间注意。对于每个注意模块，本文设计了一个覆盖所有位置的注意掩模，以抑制可能的噪声并突出正确的语义特征区域。

2. RELATED WORK

2.1 多分支架构

多分支架构背后的原理是“分裂-转换-合并”，即split-transform-merge，这降低了训练数百层网络的难度。
InceptionNet系列是成功的多分支架构，其中每个分支都精心配置了自定义的内核过滤器，以便聚合更多信息和多种功能；ResNets也可以看作是两个分支网络，其中一个分支是身份映射；SKNets和ShuffleNet系列都遵循了InceptionNets的思想，为多个分支提供了各种过滤器，但SKNets利用自适应选择机制来实现神经元的自适应感受野大小，ShuffleNets进一步将channel split和channel shuffle操作合并为单元素操作，以在速度和准确性之间进行权衡。

2.2 特征分组

特征分组学习可追溯至AlexNet，其动机是将模型分配至更多的GPU上。
MobileNets和ShuffleNets将每个通道视为一个组；CapsuleNets将每个分组神经元建模为一个capsule，其中活动capsule中的神经元代表图像中特定实体的各种属性；SGE优化了CapsuleNets，按通道维度划分多个子特征来学习不同的语义。

2.3 注意力机制

注意力机制突出信心量大的特征，而抑制不太有用的特征；自注意力机制会计算一个位置的上下文，作为图像中所有位置的加权和。
SE使用2个FC层对通道关系进行建模；ECA-Net采用一维卷积生成通道权值，降低了SE的复杂度；NL(non-local)通过计算特征图中空间点的关系矩阵生成注意力图；CBAM、GCNet和SGE将空间注意和通道注意顺序结合；DANet通过将来自不同分支的两个注意力模块相加，自适应地将局部特征与其全局依赖结合起来。

3. SHUFFLE ATTENTION

3.1 Feature Grouping

给定特征图$X\in {\mathbb{R}}^{C\times H\times W}$，沿通道维度将$X$划分为$G$组，即$X=[X_1,\dots ,X_G],X_k\in {\mathbb{R}}^{\frac{C}{G}\times H\times W}$。之后，$X_k$沿通道维度分为双分支，即$X_{k1},X_{k2}\in {\mathbb{R}}^{\frac{C}{2G}\times H\times W}$。其中一个分支利用通道间的关系生成通道注意图，一个分支利用特征的空间关系生成空间注意图（详见$3.2$和$3.3$）。

3.2 Channel Attention

在此处本欲直接利用SE模块和ECA网络，但其参数过多，不适用于轻量的注意力模块。
本文对其进行改进，首先使用全局平均池化GAP嵌入全局信息，生成通道统计数据，即$s\in {\mathbb{R}}^{\frac{C}{2G}\times 1\times 1}$，其公式定义为：
$$s={\mathcal{F}}_{gp}(X_{k1})=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{X}_{k1}(i,j)$$
然后，通过一个门控机制与$sigmoid$激活函数，生成紧凑特征，其公式定义为：
$$X_{k1}^{\prime }=\sigma ({\mathcal{F}}_c(s))\cdot X_{k1}=\sigma (W_{1}s+b_1)\cdot X_{k1}$$
其中，$W_1,b_1\in {\mathbb{R}}^{\frac{C}{2G}\times 1\times 1}$，用于缩放和移动参数。

3.3 Spatial Attention

空间注意与通道注意互补。
首先，对$X_{k2}$使用组归一化GN获得空间统计，然后采用${\mathcal{F}}_c(\cdot )$增强$X_{k2}$，空间注意的最终输出如下：
$$X_{k2}^{\prime }=\sigma (W_2\cdot GN(X_{k2})+b_2)\cdot X_{k2}$$
其中，$W_2,b_2\in {\mathbb{R}}^{\frac{C}{2G}\times 1\times 1}$。
然后，将两个分支连接，是通道数等于输入数，即$X_k^{\prime }=[X_{k1}^{\prime },X_{k2}^{\prime }]\in {\mathbb{R}}^{\frac{C}{G}\times H\times W}$

3.4 Aggregation

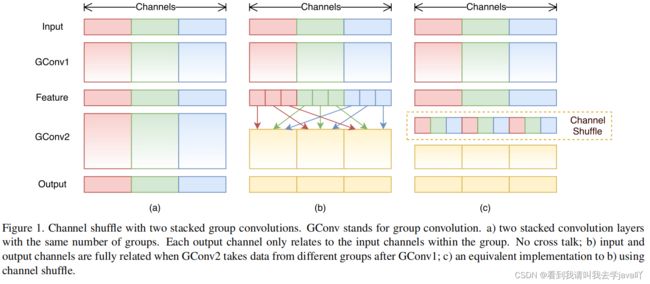
与shuffle v2类似，采用channel shuffle操作，使组间信息沿通道维度流动。SA模块的最终输出与$X$同尺寸，这使得SA模块易于与其他结构集成。
注意，$W_1,W_2,b_1,b_2$和GN的超参数只在SA模块中。在这个SA模块中，每个分支的通道数是$\frac{C}{2G}$，因此，总参数量是$\frac{3C}{G}$，$G$通常取32或64，因而SA模块非常轻量。

3.5 SA-Net for Deep CNNs

为了将SA引入深度卷积中，可使用与SENet相同的配置，只是将SE替换为SA，生成的网络命名为SA-Net。

class sa_layer(nn.Module):
    """Constructs a Channel Spatial Group module.

    Args:
        k_size: Adaptive selection of kernel size
    """

    def __init__(self, channel, groups=64):
        super(sa_layer, self).__init__()
        self.groups = groups
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.cweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.cbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))
        self.sweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1))
        self.sbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1))

        self.sigmoid = nn.Sigmoid()
        self.gn = nn.GroupNorm(channel // (2 * groups), channel // (2 * groups))

    @staticmethod
    def channel_shuffle(x, groups):
        b, c, h, w = x.shape

        x = x.reshape(b, groups, -1, h, w)
        x = x.permute(0, 2, 1, 3, 4)

        # flatten
        x = x.reshape(b, -1, h, w)

        return x

    def forward(self, x):
        b, c, h, w = x.shape

        x = x.reshape(b * self.groups, -1, h, w)
        x_0, x_1 = x.chunk(2, dim=1)

        # channel attention
        xn = self.avg_pool(x_0)
        xn = self.cweight * xn + self.cbias
        xn = x_0 * self.sigmoid(xn)

        # spatial attention
        xs = self.gn(x_1)
        xs = self.sweight * xs + self.sbias
        xs = x_1 * self.sigmoid(xs)

        # concatenate along channel axis
        out = torch.cat([xn, xs], dim=1)
        out = out.reshape(b, -1, h, w)

        out = self.channel_shuffle(out, 2)
        return out

浅析ShuffleNet

参考阿b视频
参考博客
神经网络的设计需要考虑准确度，还要注意衡量计算复杂度。目前计算复杂度的间接指标是浮点运算数，即FLOPs。然而衡量计算复杂度的直接指标，如速度，也取决于其他因素，如内存访问成本MAC和平台特性（如GPU和CPU）。因此，ShuffleNet的作者提出在目标平台上评估直接指标，而不是只考虑FLOPs。

• 整理：为什么不能用FLOPs衡量速度？

1. 其中一个因素是内存访问成本MAC。MAC在某些操作中占据了运行时间的很大一部分，在具有强大计算能力的设备（如GPU）中，MAC更为突出。
2. 并行度。在相同的FLOPs下，并行计算的速度要比串行计算的速度快的多。
3. 具有相同FLOPs的操作在不同平台上会有不同的运行时间。

ShuffleNet的作者经过分析，针对速度，提出高效网络架构设计的4个实用指南：

1. 当卷积层的输入特征与输出特征的channel相等时，MAC最小。
2. 当组卷积的分组增加时，MAC也会增大。
3. 网络设计的碎片化程度越高（包括串行与并行模块），速度越慢。
4. 逐元素操作的计算成本不可忽视。

基于上述准则，建立高效的网络架构时应遵循以下准则：

1. 通道数保持一致
2. 意识到组卷积的使用成本
3. 减少碎片化的程度（即串行和并行模块）
4. 减少逐元素运算

下图为ShuffleNet v1架构图：

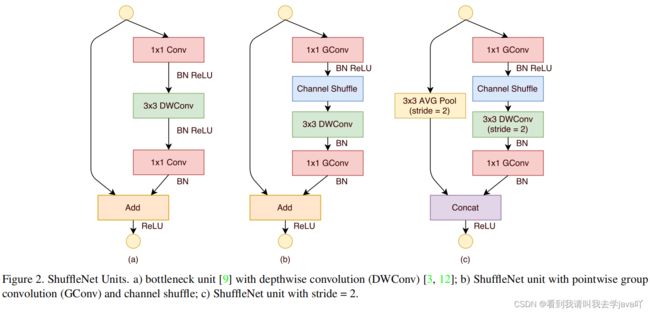
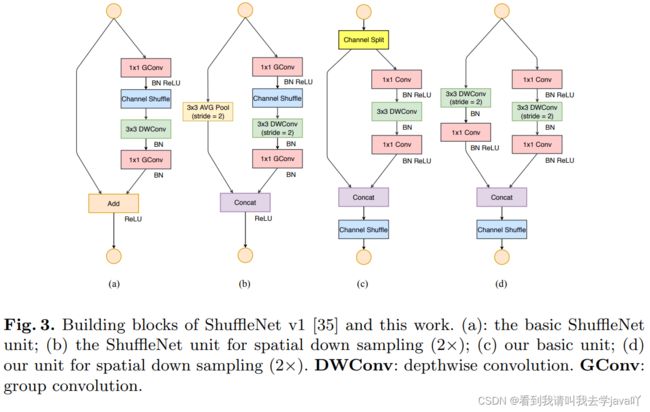
起初，只设计一个残差块，后在残差块的基础上，将卷积替换为计算复杂度更低的DWConv，即图(a)；将逐点卷积替换为组卷积，在第一个组卷积后加入channel shuffle，即图(b)；卷积神经网络需要降采样的操作，一种方式采用最大池化层，另一种方式使用$stride=2$的卷积实现，即图©，此时融合没有采取相加，而是通道拼接，可降低计算复杂度扩大通道维度。

其中，channel shuffle操作如下：

下图为ShuffleNet两代演化图：