【cv】图像预处理技术——从特征检测讲述图像预处理理论、实践、应用|01

• 博主简介：努力学习的22级计算机科学与技术本科生
• 博主主页： @是瑶瑶子啦
• 每日一言: 每一个不曾起舞的日子，都是对生命的辜负。——尼采

前言

• 回顾：
  在前一篇中【计算机视觉】图像的获取和表示——图像传感器技术|主要参数解析、成像原理剖析、传感器处理我们主要学习了计算机是如何通过图像传感器来获取图像和经过传感器处理来展现图像的（image capture and representation)。这是计算机视觉的基础，因为今天讲到的图像预处理本质上就是对矩阵的一系列运算，前一篇我们差不多弄清楚图像(即一个个像素点组成的矩阵），是如何从光，被传感器捕获，经过数模转换以及传感器处理一步一步得来的。

今天要讲的图像预处理，处理的是什么呢？也就是上一篇中讲到的经过成像系统得到的原始像素点矩阵，即原始图像数据。为什么要处理呢？这也是本文的重点，因为进行处理势必就篡改了原始数据的真实性，但是在某些情况下，经过预处理，才能更好的解决我们的问题——本文将从特征提取、检测出发，来讲述图像预处理以及带来的好处。

0、特征检测、特征提取、特征描述、特征匹配

因为学到这里使对于什么是特征检测、特征提取、特征描述、特征匹配等概念脑海中还不是很清楚，经过一些搜索学习之后，特将整理在此，如果对这四个概念比较清晰的小伙伴可以跳过这一part，只需要明白：图像预处理的目的是为了更好的特征提取而准备图像

传统图像处理中图像特征匹配有三个基本步骤：特征检测和提取(（Feature Detect）)、特征描述(特征描述（Feature Descriptor）)和特征匹配（Feature Match）。

• 特征检测提取就是从图像中提取出关键点（或特征点、角点）等。
• 特征描述就是用一组数学向量对特征点进行描述，其主要保证不同的向量和不同的特征点之间是一种对应的关系（这个向量其实就是卷积神经网络里的这个卷积核，不同的卷积核就代表/描述了不同的图像模式、特征，若某个图像与此卷积核卷积出来的值大，说明这个图像越接近与此卷积核），同时相似的关键点之间的差异尽可能小
• 特征匹配其实就是特征向量之间的距离计算，常用的距离有欧氏距离、汉明距离、余弦距离等。

一、图像预处理概述

前面说过，本文将从特征检测和特征描述的角度来讲述图像预处理，图像预处理会对特征提取的效果和图像分析的结果有很大的影响，因为直接从成像系统中获取的原始图像，很难达到很好的计算机视觉效果，而通过一个或者一系列图像预处理操作可以改善这个问题。（例如SIFT算法如果使用灰度数据的局部二值描述子，则需要将图像预处理成灰度图像，且在此基础上如果想获得更好的特征检测效果，还需要微调图像预处理）

此篇文章将基于计算机视觉领域的四类基本特征描述子来讨论图像预处理：

• （1）局部二值化描述子（LBP、ORB、FREAK等）
• （2）谱描述子（SIFT、SURF等）
• （3）基空间描述子（FFT、wavelets等）
• （4）多边形描述子（BLOB目标面积、周长、质心）

ps:基于篇幅原因，此篇博文主要介绍了图像预处理的一些方法，至于如何将图像预处理和这四个特征检测方法相结合，放在了下一篇

ps:图中画了X的表示这种预处理是有必要的

可以看到，图像预处理操作还是有很多种的，下面将对这其中的常见的预处理操作进行简单介绍分析（这里就先不结合四种特征描述方法来具体讲，结合特征描述的详细讲解将放在后面，这里主要讲解一下这些预处理操作的带来的一些效果）

二、图像预处理操作简介

这里将后续代码所需要的头文件给出，后续代码中就不再写进去了（默认已经引入）

import cv2
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.pylab as plt
import numpy as np
from skimage.io import imread
import cv2
import scipy.fftpack as fp
from PIL import Image

2.1：光照校正（直方图均衡，增强对比度）

光照会引起较深的阴影，从而遮挡局部纹理和结构，或者整场景的光照不均匀可能会扭曲成像接股票。
一些光照校正的方法：

• 秩滤波(rank filtering)
• 直方图均衡（这两篇博客对所有方法总结和原理讲解的比较到位:https://zhuanlan.zhihu.com/p/150381937、https://blog.csdn.net/qq_34107425/article/details/107503132
• LUT重映射

2.1.1：直方图均衡HE（Histogram Equalization）

基本思想：保持像素数量不变，将像素进行重新分配，使每个灰度级上对应的像素数量差别不大。

算法思路：
上面博客对具体算法分析的比较详细，这里给出我自己的理解画出示意图来帮助理解。核心就是：找到两个直方图之间的映射关系，对不同像素值的像素进行映射（即重新分配这些“长条”，但长度（即一个像素值对应的像素数）和总像素数不变），目的是使这些长条能尽可能均匀分布在直方图上，而不是集中在某一块。

y = f(x) 简单理解： 在均衡前原始直方图中，像素值为x的像素，经过f这个映射关系后，像素值为x的像素，像素值改为y。对原始图像中所有像素值进行这样映射，然后得到右边的直方图，这个过程就是直方图均衡。目的是使像素在各个像素值上分配比较均匀。

下面依次是：原图、对比度拉伸、直方图均衡带来的效果

特征：

可以看到直方图均衡能较好的增强图像对比度，凸显细节，但是也存在以下的一些问题，在上面给出的参考博客中已经做出详细分析，这里根据我自己的理解再简单概括一下。

• 分色现象：当图像颜色值比较单一且离得比较近（颜色值比较相似），进行直方图均衡后，会导致这些颜色值离得比较远，从而使本来颜色值差别不大的一张图像出现颜色分层的现象。

• 对齐问题:直方图均衡的一个重要特征是把原图中最亮的像素对齐到预设的最大值（比如8bit图是255）。当颜色比较丰富时，这样做影响不大。当颜色比较单一，就像上面图示一样，一个颜色可能会从一个值跨越很大变成另外一种颜色。比如原图中所有像素都是一个值（例如8，这对应一幅纯黑的图像，多半是拍摄于夜间），则均衡之后所有像素都被映射到255，图像变成了纯白的。
• 噪声问题:根源还是对其问题，如果一张较暗的图像中有白色噪声，经过直方图均衡后，这些噪声将更加明显。
  

2.1.2：自适应直方图均衡AHE

自适应直方图均衡 Adaptive Histogram Equalization（AHE)

如果用两个词来简单区分一下自适应直方图均衡（AHE）和前面讲的直方图均衡（HE),我现在脑子里面的两个词是：局部、全局。

直方图是对整个图像进行直方图均衡，而自适应直方图则是对局部进行均衡。它会把图像分成几个小块，进行独自的均衡。这种均衡方法更容易突出细节，增强图像边缘信息。

但是自适应直方图均衡并没有解决直方图均衡中的噪声问题。
而且得出来的图像会比较不连续

2.1.3：限制对比度自适应直方图均衡 CLAHE

这个时候人们又想出了更好的方法。你不是说直方图均衡存在对齐问题嘛，在图像颜色值比较集中在一点时（某一个颜色值的像素数很多），会突然把这么多的像素啪的一下从这个颜色值移到另外一个，虽然增强也增强了对比度，但是会带来分色现象和扩大噪声的影响。

我们再仔细想想上面所说的那个问题的本质是什么？对，某一个颜色值/灰度值对应的像素数太多啦，导致其他颜色值都没多少像素。

基本思想：CLANE算法的思想就是在自适应直方图均衡的基础上，限制一下：某一个颜色值的像素数（频数）太多了（通常会指定一个阈值），不行，给我匀点到其他像素值上去一些像素。

这样总算是优化了直方图均衡中的：分色问题、噪声问题等。

等等，还有一个问题：不连续。

为了解决这个问题，提出了优化方案双线性插值的AHE，然后这个基础上再使用CLHE的截断对比度的思想，就变成了我们现在的CLAHE算法。

使用双线性插值的方案的CLAHE算法

1. 将图像分成很多个子区域，对每个子区域分别计算其各自的灰度直方图和累计分布函数
2. 将原始图像中的像素按照分布分为三种情况处理：
   a. 红色区域中的像素按照其所在子图的变换函数进行灰度映射
   b. 绿色区域中的像素按照所在的两个相邻子图变换函数变换后进行线性插值得到
   c. 紫色区域中的像素按照其所在的四个相邻子图变换函数变换后双线性插值得到

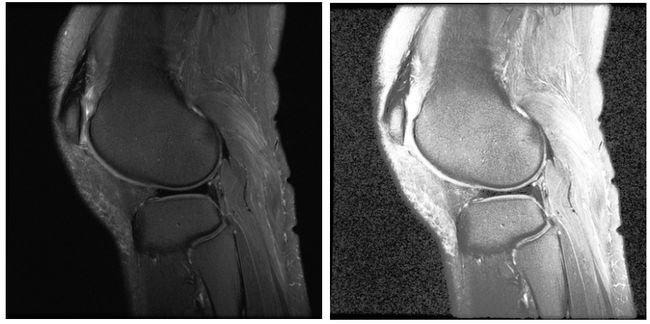
CLAHE算法的应用：对于医学图像，特别是医学红外图像的增强效果非常明显:这篇博客做出了非常详细的讲解CLAHE的实现和研究
这里放两张出自这篇博客的对比图感受一下：

2.1.4：代码实例

# 读取图片
image_path = r'E:\1_Technological_Capability\Algorithm\CV\Projects\HSR\My_Work\Jie_Net\Learning\004401893_K1385515_1428_0_46.jpg'
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)  # 以灰度图像格式读取图片

# 进行直方图均衡化
equalized_image = cv2.equalizeHist(image)

# 进行自适应直方图均衡化增强
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
enhanced_image = clahe.apply(image)

def plt_def():
    # 显示原始图片、直方图均衡化后的图片和增强后的图片
    plt.figure(figsize=(15, 5))

    plt.subplot(1, 3, 1)
    plt.imshow(image, cmap='gray')
    plt.title('Original Image')

    plt.subplot(1, 3, 2)
    plt.imshow(equalized_image, cmap='gray')
    plt.title('Equalized Image')

    plt.subplot(1, 3, 3)
    plt.imshow(enhanced_image, cmap='gray')
    plt.title('Enhanced Image')

    plt.tight_layout()
    plt.show()
plt_def()

在CLAHE算法的核心部分可以看到有两个参数：

• clip_limit:也就是上面那张图的Nominal clipping level p.我们不是讲过，在这种限制对比度的方法中，如果某个bin的像素频数超过某一阈值，就需要裁剪掉嘛，把超出部分平均分配到其他的bins上，以达到限制对比度的目的。而clip_limit就是指的这个阈值。
• tilesGridSize：图像被分成称为“tiles”（瓷砖、地砖、小方地毯、片状材料、块状材料）的小块，在OpenCV中，tilesGridSize默认为8x8 ，即整个图像被划分为8纵8横共64块。然后对每一个块进行直方图均衡处理

2.2：模糊（平滑）

首先说模糊把，焦点校正算是模糊的其中一个应用。我个人目前学习到的模糊（平滑）操作的应用

• 去噪
• 目标提取

2.2.1：去噪和滤波

通过模糊操作（或者称平滑操作，可以去除噪声），得到更平滑的图像，避免噪声干扰，方便后续图像处理。

当然去噪的方法有很多很多种，可以参考下面该图：

我目前了解、接触和用过的是我框起来来的哲学，而在本节中，即图像平滑，我将对空间域滤波的最常见两种滤波：——均值滤波、高斯滤波、中值滤波进行讲解。（具体深入了解图像去噪，这里可以参考这篇博客，这里记下方便后续学习：https://blog.csdn.net/qq_33208851/article/details/97123411)

2.2.1.1:均值滤波

• 均值滤波
  • 原理：即定义一个nxn的核，对核中像素算平均值，然后将平均值赋给中心像素。
    
  • 代码实现和效果：
    在OpenCV中，实现均值滤波的函数是cv2.blur（）其语法格式为 dst=cv2.blur（src,ksize,anchor,borderType）
    ● dst是返回值，表示进行均值滤波后得到的处理结果。
    ● src 是需要处理的图像，即原始图像。它可以有任意数量的通道，并能对各个通道独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一种。
    ● ksize是滤波核的大小。滤波核大小是指在均值处理过程中，其邻域图像的高度和宽度。滤波核越大，去噪效果更佳，但是图像越模糊；滤波核越小，图像相对清晰，但去噪不佳。
    ● anchor 是锚点，其默认值是（-1,-1），表示当前计算均值的点位于核的中心点位置。该值使用默认值即可，在特殊情况下可以指定不同的点作为锚点。
    ● borderType是边界样式，该值决定了以何种方式处理边界。一般情况下不需要考虑该值的取值，直接采用默认值即可。
    通常情况下，使用均值滤波函数时，对于锚点anchor和边界样式borderType，直接采用其默认值即可。

# 加载图像
image_path = r"F:\AI\Learning\yyz.png"
image = cv2.imread(image_path)

# 将图像转换为RGB（OpenCV读取的图像为BGR）
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 添加椒盐噪声
def add_salt_and_pepper_noise(image, salt_prob, pepper_prob):
    noisy_image = np.copy(image)
    total_pixels = image.size

    # 添加盐噪声
    num_salt = np.ceil(salt_prob * total_pixels)
    salt_coords = np.random.choice(range(image.size), size=int(num_salt), replace=False)
    noisy_image.flat[salt_coords] = 255

    # 添加椒噪声
    num_pepper = np.ceil(pepper_prob * total_pixels)
    pepper_coords = np.random.choice(range(image.size), size=int(num_pepper), replace=False)
    noisy_image.flat[pepper_coords] = 0

    return noisy_image

# 添加椒盐噪声
salt_prob = 0.01  # 盐噪声概率
pepper_prob = 0.01  # 椒噪声概率
noisy_image = add_salt_and_pepper_noise(image_rgb, salt_prob, pepper_prob)

# 使用均值滤波去噪
denoised_image = cv2.blur(noisy_image.astype('uint8'), (6, 6))
def plt_def():
    # 显示原始图像、带噪声的图像和去噪图像
    plt.figure(figsize=(15, 30))

    plt.subplot(131)
    plt.imshow(image_rgb)
    plt.title('Original Image')
    plt.axis('off')

    plt.subplot(132)
    plt.imshow(noisy_image)
    plt.title('Noisy Image')
    plt.axis('off')

    plt.subplot(133)
    plt.imshow(denoised_image)
    plt.title('Denoised Image')
    plt.axis('off')

    plt.show()
plt_def()

改为小一点的3x3滤波核

2.2.1.2高斯滤波

前面讲的均值滤波是简单粗暴的平均对一个点周围像素进行求平均，但是实际上，一个点与周围的关系和距离也有关系。距离越远，关系越小，权重也更小，距离越近，影响和关系越大，权重也越大。

符合这种描述的是高斯函数，而运用这种理念的也就是高斯滤波：

• 基本原理：

  • 找到高斯模板，模板（mask在查阅中有的地方也称作掩膜或者是高斯核），高斯函数 生成
  • 利用高斯模板进行卷积
    
    至于如何利用高斯函数生成模板以及优化等，可以参考这篇博客的讲解:https://blog.csdn.net/a435262767/article/details/107115249

• 在OpenCV中，实现高斯滤波的函数是cv2.GaussianBlur（），该函数的语法格式是dst=cv2.GaussianBlur（src,ksize,sigmaX,sigmaY,borderType）

  ● dst是返回值，表示进行高斯滤波后得到的处理结果。
  ● src 是需要处理的图像，即原始图像。它能够有任意数量的通道，并能对各个通道 独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一 种。
  ● ksize 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽 度。需要注意，滤波核的值必须是奇数。
  ● sigmaX 是卷积核在水平方向上（X 轴方向）的标准差，其控制的是权重比例。
  ● sigmaY是卷积核在垂直方向上（Y轴方向）的标准差。如果将该值设置为0，则只采用sigmaX的值
  如果sigmaX和sigmaY都是0，则通过ksize.width和ksize.height计算得到。其中sigmaX=0.3×[（ksize.width-1）×0.5-1] +0.8
  sigmaY=0.3×[（ksize.height-1）×0.5-1]+0.8
  ● borderType是边界样式，该值决定了以何种方式处理边界。一般情况下，不需要考虑该值，直接采用默认值即可。 在该函数中，sigmaY和borderType是可选参数。sigmaX是必选参数，但是可以将该参数设置为0，让函数自己去计算sigmaX的具体值。

函数cv2.GaussianBlur（）的常用形式为： dst=cv2.GaussianBlur（src,ksize,0,0）

# 加载图像
image_path = r"F:\AI\Learning\yyz.png"
image = cv2.imread(image_path)

# 将图像转换为RGB（OpenCV读取的图像为BGR）
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 对图像添加高斯噪声
def add_gauss_noise(image, mean=0, val=0.01):
    size = image.shape
    # 对图像归一化处理
    image = image / 255.0
    gauss = np.random.normal(mean, val**0.05, size)
    image = image + gauss
    return image

noisy_image = add_gauss_noise(image_rgb)

# 高斯滤波
denoised_image = cv2.GaussianBlur(noisy_image, (5, 5), 0) 
def plt_def():
    # 显示原始图像、带噪声的图像和去噪图像
    plt.figure(figsize=(15, 30))

    plt.subplot(131)
    plt.imshow(image_rgb)
    plt.title('Original Image')
    plt.axis('off')

    plt.subplot(132)
    plt.imshow(noisy_image)
    plt.title('Noisy Image')
    plt.axis('off')

    plt.subplot(133)
    plt.imshow(denoised_image)
    plt.title('Denoised Image')
    plt.axis('off')

    plt.show()
plt_def()

2.2.1.3:中值滤波

前面讲到的均值滤波、高斯滤波，它们的策略都是将一个点周围的像素点的像素信息都考虑进来，进行加权求和的方法来得到该点的像素值，这些方法都是线性方法。缺点是噪声信息也会被考虑进来（虽然说相较于原图像，噪声已经变得柔和了许多）。

这一小节学习的方法是中值滤波，它是一种非线性的方法。

• 基本原理： 同样还是有一个nxn的核，这次，对于这个核像素点的取值，就不是对nxn个像素值进行加权求和了，而是把这nxn个像素值排个序，找出中间那个值，赋给当前像素点。
  
  比如在上面该图中，对九个点按照大小进行排序，中值是93，那么经过中值滤波后，该点的像素值就是93
  

• opencv中值滤波的实现： dst=cv2.medianBlur（src,ksize）

  • dst是返回值，表示进行中值滤波后得到的处理结果。
  • src 是需要处理的图像，即源图像。它能够有任意数量的通道，并能对各个通道独立处理。图像深度应该是CV_8U、CV_16U、CV_16S、CV_32F 或者 CV_64F中的一种。
  • ksize 是滤波核的大小。滤波核大小是指在滤波处理过程中其邻域图像的高度和宽度。需要注意，核大小必须是比1大的奇数，比如3、5、7等。

# 加载图像
image_path = r"F:\AI\Learning\yyz.png"
image = cv2.imread(image_path)

# 将图像转换为RGB（OpenCV读取的图像为BGR）
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 添加椒盐噪声
def add_salt_and_pepper_noise(image, salt_prob, pepper_prob):
    noisy_image = np.copy(image)
    total_pixels = image.size

    # 添加盐噪声
    num_salt = np.ceil(salt_prob * total_pixels)
    salt_coords = np.random.choice(range(image.size), size=int(num_salt), replace=False)
    noisy_image.flat[salt_coords] = 255

    # 添加椒噪声
    num_pepper = np.ceil(pepper_prob * total_pixels)
    pepper_coords = np.random.choice(range(image.size), size=int(num_pepper), replace=False)
    noisy_image.flat[pepper_coords] = 0

    return noisy_image



# 添加椒盐噪声
salt_prob = 0.1  # 盐噪声概率
pepper_prob = 0.1  # 椒噪声概率
noisy_image = add_salt_and_pepper_noise(image_rgb, salt_prob, pepper_prob)

# 使用中值滤波去噪
denoised_image = cv2.medianBlur(noisy_image, 3)
def plt_def():
    # 显示原始图像、带噪声的图像和去噪图像
    plt.figure(figsize=(15, 30))

    plt.subplot(131)
    plt.imshow(image_rgb)
    plt.title('Original Image')
    plt.axis('off')

    plt.subplot(132)
    plt.imshow(noisy_image)
    plt.title('Noisy Image')
    plt.axis('off')

    plt.subplot(133)
    plt.imshow(denoised_image)
    plt.title('Denoised Image')
    plt.axis('off')

    plt.show()
plt_def()

2.2.1.4：总结

前面的三种方法，均值滤波核高斯滤波属于对图像空间进行加权平均的线性操作，它们的共同点都是有一个核，其实就是一个系数矩阵，被称作空间滤波器，用于在图像的二维空间进行线性操作。

由于经过滤波器滤波后，噪声会变得柔和，它们也被称为平滑滤波器。

以后我们看到模板、核、卷积核、窗口、滤波器、空间滤波器等等术语，都指的是这个东西。当然，卷积的真实含义与这里的操作有一点点的区别，但不必过于拘泥于术语的精确性

2.2.2：目标提取

通过平滑滤波器，可以实现降噪，这是前面已经讲到的。但降噪只是它的一个应用。

模糊操作还有一个应用，就是目标提取。

基本原理： 通过空间滤波器，模糊掉小的、不感兴趣、亮度较高物体（类比于上面的“噪声”），然后再结合下面即将要讲到的二值化，对图像进行二值化操作，提取到大的、目标物体，过滤掉尺寸小，亮度高的物体。

这里给出一个例子：参考自https://blog.csdn.net/saltriver/article/details/78883989
下面是一张哈勃望远镜拍摄的星空原始图像(来自冈萨雷斯的《数字图像处理)

经过平滑滤波器后：

再对模糊的图像进行设定阈值的二值化：

2.3：图像金字塔

在上面学习模糊、滤波、去噪等操作时，了解到了还有一种叫做图像金字塔的概念，去大概学习和了解了一下。

• 应用主要是：压缩和图像拼接。

压缩可能会用得到（降低图像分辨率）

具体的原理等，这里先给出学习的博客，等以后需要应用或者深入学习的时候，再来填这个坑。

• https://blog.csdn.net/zaishuiyifangxym/article/details/90167880(这个对于向上向下采样介绍的比较好）
• https://zhuanlan.zhihu.com/p/80362140:拉普拉斯金字塔的构建过程
• https://blog.csdn.net/bby1987/article/details/129271241:应用：图像融合
• https://zhuanlan.zhihu.com/p/454085730:应用：图像压缩+融合

2.4：边缘提取和边缘增强

本小节的讲解参考：https://zhuanlan.zhihu.com/p/343858207

目的：增强图像的边缘，突出细节
一些图像经过上面的平滑滤波器进行去噪之后，会变得模糊。而边缘增强/锐化则是增强图像边界和细节，这个时候我们利用的滤波器就叫做:“平滑滤波器”

基本原理：:

• 图像边缘:
  首先要明白什么是图像边缘，它的特征，由此来对其进行增强。区别一个物体主要是通过边缘，边缘处的往往像素值变化比较大，我们就是根据这种差异，进行差分操作来增强边缘信息。

  • 求一定区间的变化大小，在连续区间是微分运算，对应离散区间也就是差分（因为数字图像是离散的，这里用差分定义微分）
  • 求变化的快慢大小，就是求二阶导，在二维空间对应的就是梯度运算

• 边缘分类：（注意，边缘也有方向之分，下面展示的例子只是水平x方向的边缘而已）
  

  • 阶梯状特点：对于一个阶跃边缘点，其灰度变化曲线的一阶导数在该点达到极大值, 二阶导数在该点与零交叉（一阶导数与二阶导数的意义）
  • 脉冲状特点：一阶导数有最大有最小，过0点
  • 屋顶状特点： 对于一个屋顶边缘点，其灰度变化曲线的一阶导数在该点与零交叉（因为该点为一个局部最大值点）；二阶导数在该点绝对值达到极大值。

• 一阶微分算子和二阶微分算子
  - 简单来说，一阶微分算子就是求该方向的一一阶导数，而二阶微分算子是表示该方向的二阶导数
  
  
  在图像处理里面，因为信息是以矩阵的形式存在，我们要根据上面表达式构造同意义差分矩阵，也就是 构造差分模板、核，从而对图像矩阵进行差分(微分）/梯度运算，从而得到/提取到边缘信息。

• 微分运算

  • 单向微分运算：
    分为:竖直方向微分，水平方向微分,作用是提取竖直/水平方向的边界
  • 双向一次微分运算：
    即对原图像进行一次竖直微分，再对原图像进行一次垂直微分，对两次微分分别取平方再相加。
  • 作用
    • 该点像素值大小反映变化大小
    • 像素值不变的区域经过微分（差分）运算结果是0，颜色体现上是黑色
    • 像素值变化剧烈的区域，相减后得到较大的变化率，像素灰度值变化差别越大，则得到的像素就越亮，图像的边缘得到增强

• 梯度运算
  上面的微分运算对颜色变化的方向性局限比较大，只能水平或者竖直，而梯度我们知道，它是一个向量，有方向。分别沿着X和Y计算；在X方向求一次微分，得到G(x);在Y方向求一次微分，得到G(y).这样就构成了矢量

  梯度是矢量，我们需要变成标量，一个可测的量；将X和Y分别取绝对值相加，直接得到梯度，或者把这两个值取最大值，或者对这两个值，平方在开方；就得到梯度；
  （我个人现在感觉，梯度本身是有方向的，但是它这样把他化成标量之后，感觉核上面讲的双向一次微分又没有区别了，好像也不能体现方向性，本质上还是在x,y方向上进行微分）
  

• 交叉微分运算

  • 这次的微分不再是水平和竖直方向了，而是换成了在一个斜边方向
    

下面根据具体的微分模板，来讲解不同的锐化算法，它们的作用是提取边缘信息，它们的本质还是上面说的三种运算

2.4.1：sobel算法

• 模板和梯度计算
  
• 思想：sobel算法认为，距离中心点的距离对边缘检测影响不同，距离越近影响越大，所以看到z2,和z8的值要比其他四个大一些
• 原理：对传入进来的图像（其实就是一个像素矩阵）进行微分计算，得到Gx,和Gy，然后根据二者计算梯度（转化后的标量）；然后对生成的新像素灰度值做阈值运算，以此来确定边缘信息。（卷积核也可以旋转，用与查找不与x,y轴平行或垂直的方向上的边缘）
• 特点：下一行数据平均化减去上一行数据平均化的值；下一列数据平均化减去上一列数据平均化的值，先平滑然后微分。有抑制噪声的作用

2.4.2：Prewitt算法

Prewitt算子同样也是一种一阶微分算子。

和sobel算法唯一不同在系数上面，它不强调距离远近的影响

2.4.3：拉普拉斯算法

前面讲的两种算法都是一阶微分算法，而下面要讲的是laplacian是一种二阶微分算法。

• 二阶微分和梯度的计算
  
• 对应的卷积核/模板
  
• 运算特点：
  因为它是二阶微分，它注重变化的快慢。所以，它强调突变，而弱化慢变。产生一副把浅灰色边线、突变点叠加到暗背景中的一副图像

2.4.4：边缘增强

前面讲到的三种算法，本质上都是提取边缘信息，提取到边缘信息的结果图像是一副整体比较按，边缘为白色或灰色的图像。要达到我们所想要的在保留图像原始信息的基础上，对图像进行增强，需要将边缘提取结果和原始图像进行叠加

根据公式推导出模板：

2.4.5：代码实例

• sobel算法

import matplotlib.pyplot as plt

# 读取图像
image_path = r"F:AI/Learning/9022625033_K1609563_T001_4_13.jpg"
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

# 使用Sobel算子进行边缘增强
sobelx = cv2.Sobel(image, cv2.CV_64F, 1, 0, ksize=3)
sobely = cv2.Sobel(image, cv2.CV_64F, 0, 1, ksize=3)
edge_enhanced_image = cv2.magnitude(sobelx, sobely) + image

def plt_def():
    # 显示图像
    plt.figure(figsize=(10, 10))

    # 原始图像
    plt.subplot(2, 2, 1)
    plt.imshow(image, cmap='gray')
    plt.title('Original Image')
    plt.axis('off')

    # 边缘增强后的图像
    plt.subplot(2, 2, 4)
    plt.imshow(edge_enhanced_image, cmap='gray')
    plt.title('Edge Enhanced Image')
    plt.axis('off')

    plt.subplot(2, 2, 2)
    plt.imshow(sobelx, cmap='gray')
    plt.title('sobelx')
    plt.axis('off')

    plt.subplot(2, 2, 3)
    plt.imshow(sobely, cmap='gray')
    plt.title('sobely')
    plt.axis('off')

    plt.tight_layout()
    plt.show()

plt_def()

• 拉普拉斯算法

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像
image_path = r"F:AI/Learning/9022625033_K1609563_T001_4_13.jpg"
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

# 应用拉普拉斯算子进行高频增强
laplacian_image = cv2.Laplacian(image, cv2.CV_64F)

# 增强高频信息
enhanced_image = image + 2*laplacian_image

def plt_def():
    # 显示图像
    plt.figure(figsize=(12, 6))

    # 原始图像
    plt.subplot(1, 3, 1)
    plt.imshow(image, cmap='gray')
    plt.title('Original Image')
    plt.axis('off')

    # 拉普拉斯算子得到的高频信息
    plt.subplot(1, 3, 2)
    plt.imshow(laplacian_image, cmap='gray')
    plt.title('Laplacian Image (High Frequency)')
    plt.axis('off')

    # 增强后的图像
    plt.subplot(1, 3, 3)
    plt.imshow(enhanced_image, cmap='gray')
    plt.title('Enhanced Image (High Frequency Enhanced)')
    plt.axis('off')

    plt.tight_layout()
    plt.show()
plt_def()

2.5：分割（二值化）

• 原理：本质上就是根据图像直方图，确定一个像素值阈值，然后对图像进行二值化，得到的图像只有两个像素取值（一般是0和255，非黑即白）

下面用代码实例展示一下：

# 读取图像
image_path =  r"E:\1_Technological_Capability\Algorithm\CV\Projects\HSR\My_Work\Jie_Net\Learning\9022625033_K1609563_T001_4_13.jpg"
# image_path =  image_path = r"E:\1_Technological_Capability\Algorithm\CV\Projects\HSR\My_Work\Jie_Net\Learning\kodim23.png"

image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)

# 使用Otsu's二值化分割图像
_, mask = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)
def plt_def():
    # 显示图像和掩码
    plt.figure(figsize=(10, 5))

    # 原始图像
    plt.subplot(1, 2, 1)
    plt.imshow(image, cmap='gray')
    plt.title('Original Image')
    plt.axis('off')

    # 生成的掩码
    plt.subplot(1, 2, 2)
    plt.imshow(mask, cmap='gray')
    plt.title('Generated Mask')
    plt.axis('off')

    plt.tight_layout()
    plt.show()
plt_def()

使用Otsu’s二值化方法对灰度图像进行阈值分割时，可以使用OpenCV中的cv2.threshold()函数。该函数将灰度图像转换为二值图像，其中像素值只能为0或255，用于表示对象和背景。

使用Otsu’s二值化方法，我们不需要手动选择阈值，而是通过算法自动确定最佳阈值，以便将图像分割为对象和背景。这种方法适用于具有双峰直方图的图像，其中双峰分别对应于对象和背景的像素值。

通过使用cv2.threshold()函数并指定阈值类型为cv2.THRESH_BINARY +
cv2.THRESH_OTSU，我们可以得到一个二值化图像，其中大于阈值的像素值为255，小于等于阈值的像素值为0。这样就实现了对灰度图像的自动阈值分割，生成了一个二值化的掩码图像，用于表示对象和背景的像素。

• 作用：方便后续处理，比如图像分割、边缘提取，图像增强，图像压缩等等

2.6：形态学

• 什么是形态学处理？
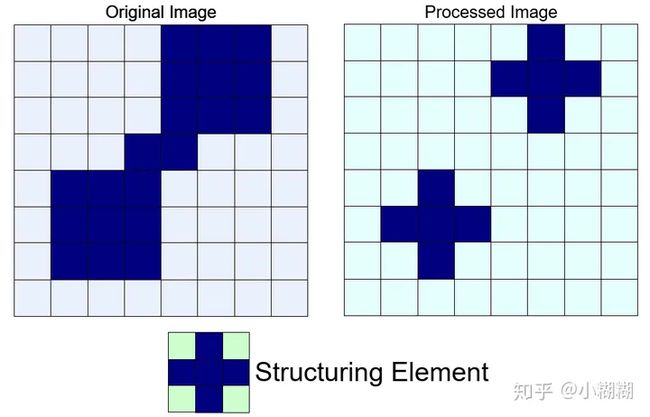
  是指一系列用来处理图像中物体形状特征的方法

  原理是利用结构元（和卷积核类似的东西，都是一个"矩阵“。但操作不是线性求和，而是逻辑运算），来处理图像中物体的形状特征

  基础是集合论（因为是做逻辑运算）

• 基本概念
  结构元（Structuring Elements，SE）可以是任意形状，SE中的的值可以是0或1。常见的结构元有矩形和十字形。结构元有一个锚点O，O一般定义为结构元的中心（也可以自由定义位置）。如下图所示是几个不同形状的结构元，紫红色区域为锚点O。
  

不做特殊说明，输入图像为二值图像。图像中1是前景，0是背景。记 f为原图像， s为结构元

• 膨胀（Dilation）
  将结构元s在图像f上移动，若结构元中为1的位置对应原图像相应位置中像素值最大的赋给当前锚点。

  视觉体验如下：

  在灰度图像中简记为：”白吃黑“

• 腐蚀（Erosion）
  将结构元s在图像f上移动，若结构元中为1的位置对应原图像相应位置中像素值最小的赋给当前锚点。

  视觉体验如下：

  在灰度图像中简记为：”黑吃白“
  

• 开运算（Opening）
  先腐蚀，再膨胀，视觉体验效果如下，像”断开“一样
  

• 闭运算（Closing）
  先膨胀再腐蚀，视觉效果：闭合
  

• 代码实例
  下面我利用膨胀操作，将有影响作用的螺丝给膨胀掉，然后使用腐蚀，还原圆孔大小

# 读取图像
image_path = r"F:/AI/wheelData/VOC2007_LK/JPEGImages/LK0002.png"
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# 创建形态学操作的结构元素（这里使用一个3x3的正方形结构元素）
kernel = np.ones((3, 3), np.uint8)
# 膨胀操作
dilated_image = cv2.dilate(image, kernel, iterations=6)
# 对膨胀后的图像进行腐蚀操作
eroded_image = cv2.erode(dilated_image, kernel, iterations=7)
def plt_def():
    # 显示图像
    plt.figure(figsize=(12, 6))

    # 原始图像
    plt.subplot(1, 3, 1)
    plt.imshow(image, cmap='gray')
    plt.title('Original Image')
    plt.axis('off')

    # 膨胀后的图像
    plt.subplot(1, 3, 2)
    plt.imshow(dilated_image, cmap='gray')
    plt.title('Dilated Image')
    plt.axis('off')

    # 腐蚀后的图像
    plt.subplot(1, 3, 3)
    plt.imshow(eroded_image, cmap='gray')
    plt.title('Eroded Image')
    plt.axis('off')

    plt.tight_layout()
    plt.show()
plt_def()

2.7：色彩空间转换

import cv2
import matplotlib.pyplot as plt

# 读取RGB图像
image_path = r"F:\AI\Learning\kodim23.png"
image = cv2.imread(image_path)
image_rgb = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)  # 转换为RGB

# 转换为其他颜色空间
image_bgr = image  # BGR格式
image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)  # 灰度图
image_hsv = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)  # HSV
image_ycrcb = cv2.cvtColor(image, cv2.COLOR_BGR2YCrCb)  # YCrCb
image_hls = cv2.cvtColor(image, cv2.COLOR_BGR2HLS)  # HLS
image_xyz = cv2.cvtColor(image, cv2.COLOR_BGR2XYZ)  # XYZ
image_lab = cv2.cvtColor(image, cv2.COLOR_BGR2LAB)  # LAB
image_yuv = cv2.cvtColor(image, cv2.COLOR_BGR2YUV)  # YUV

def plt_def():
    # 显示图像
    plt.figure(figsize=(14, 10))

    plt.subplot(3, 3, 1)
    plt.imshow(image_rgb)
    plt.title('RGB')
    plt.axis('off')

    plt.subplot(3, 3, 2)
    plt.imshow(image_bgr)
    plt.title('BGR')
    plt.axis('off')

    plt.subplot(3, 3, 3)
    plt.imshow(image_gray, cmap='gray')
    plt.title('GRAY')
    plt.axis('off')

    plt.subplot(3, 3, 4)
    plt.imshow(image_hsv)
    plt.title('HSV')
    plt.axis('off')

    plt.subplot(3, 3, 5)
    plt.imshow(image_ycrcb)
    plt.title('YCrCb')
    plt.axis('off')

    plt.subplot(3, 3, 6)
    plt.imshow(image_hls)
    plt.title('HLS')
    plt.axis('off')

    plt.subplot(3, 3, 7)
    plt.imshow(image_xyz)
    plt.title('XYZ')
    plt.axis('off')

    plt.subplot(3, 3, 8)
    plt.imshow(image_lab)
    plt.title('LAB')
    plt.axis('off')

    plt.subplot(3, 3, 9)
    plt.imshow(image_yuv)
    plt.title('YUV')
    plt.axis('off')

    plt.tight_layout()
    plt.show()
plt_def()

三、总结

图像预处理中的数学和统计处理涵盖了多种技术和方法，旨在对图像进行数学变换、特征提取、噪声去除和增强等操作。这些处理可以用于改善图像质量、准备图像数据以供后续分析或机器学习任务使用。

以下是一些常见的数学和统计处理技术，它们常用于图像预处理：

1. 灰度变换：

   • 线性变换：如亮度和对比度调整，可以通过缩放和平移像素值范围来调整图像的明暗度和对比度。
   • 非线性变换：如伽马校正，用于调整图像的亮度响应曲线，特别对于低光照或高光照图像有用。

2. 直方图处理：

   • 直方图均衡化：用于增强图像的对比度，通过重新分布图像的像素值使直方图更均匀。
   • 直方图匹配：将图像的直方图匹配到一个特定的参考直方图，用于使图像具有参考图像的统计特性。

3. 滤波器和卷积：

   • 平滑滤波器：如高斯滤波器，用于降低图像中的噪声。
   • 锐化滤波器：如拉普拉斯滤波器，用于增强图像的边缘和细节。

4. 傅里叶变换：

   • 傅里叶变换和逆变换：用于将图像从空间域转换到频率域，可以进行频域滤波和变换。

5. 形态学处理：

   • 腐蚀和膨胀：用于图像的形态学操作，可以对图像的形状和结构进行处理，如边缘检测、物体分割等。

6. 阈值分割：

   • Otsu’s二值化：自适应阈值分割方法，可以根据图像的直方图自动选择二值化阈值，常用于图像分割。

7. 降噪：

   • 统计滤波器：如中值滤波，用于去除图像中的噪声，特别对椒盐噪声有用。
   • 小波去噪：使用小波变换来去除图像中的噪声，可以保留图像的特征。

8. 特征提取：

   • 统计特征：如图像的平均值、方差、标准差等统计量，用于描述图像的特征。
   • 几何特征：如图像的面积、周长、凸壳等几何属性。

这些数学和统计处理方法可以根据特定任务的需求进行组合和调整，以实现预期的图像预处理效果。

---

写在最后：文章内容主要来自以下参考以及个人理解、实验室学长讲解和讨论，因为个人专业能力和知识还在提升中，若文章内容有错误或有失偏颇的地方，还请大家多多指出
后续还会围绕《计算机视觉度量从特征描述到深度学习》这本书的学习持续更新相关内容

参考：

• 《Computer Vision Metrics》/《计算机视觉度量从特征描述到深度学习》
• https://zhuanlan.zhihu.com/p/150381937、
• https://blog.csdn.net/qq_34107425/article/details/107503132
• https://zhuanlan.zhihu.com/p/343858207
• https://blog.csdn.net/saltriver/article/details/78883989
• https://blog.csdn.net/qq_33208851/article/details/97123411)
• CLAHE的实现和研究