二叉树前序、中序、后序遍历总结

将力扣中二叉树遍历的三个题的题解中的不同实现方式进行总结，对应的三道题分别为：

• 144. 二叉树的前序遍历
• 94. 二叉树的中序遍历
• 145. 二叉树的后序遍历

本文使用力扣给出的二叉树的定义，如下：

struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

一、前序遍历

前序的遍历顺序为：

• 访问根结点
• 前序遍历左子树
• 前序遍历右子树

在访问左子树或右子树时，同样按照前序遍历的方式进行。

1. 递归

根据前序遍历的定义，可以看出整个遍历过程天然具有递归的性质，所以最直接的方法就是使用递归实现。

如下所示，使用 preorder(root) 表示遍历当前二叉树，由于是前序遍历，在当前二叉树的遍历中，首先将根结点加入结果，之后递归对左子树和右子树调用 preorder来遍历，当遇到空树时，递归结束。

void preorder(TreeNode *root, vector<int> &res){
	if(!root){
		return;
	}
	res.push_back(root->val);
	preorder(root->left, res);
	preorder(root->right, res);
}

vector<int> preorderTraversal(TreeNode* root){
	vector<int> result;
	preorder(root, result);
	return result;
}

复杂度分析：

• 时间复杂度：$O(n)$，$n$是节点个数，每个结点被遍历一次。
• 空间复杂度：$O(n)$，每层结点需要调用递归，递归时需要通过栈保存每次调函数的状态，所以平均情况下为 $O(\log n)$（根据树的层数计算）；最坏情况下是树为链状，为 $O(n)$。

2. DFS迭代

递归是通过函数的调用维护了一个栈，利用这个栈实现了访问每个结点，我们可以直接构建一个栈，将递归的栈模拟出来。

主要思想：
前序遍历的过程是先遍历根结点，再遍历左子树，最后遍历右子树，我们可以根据这个过程，先遍历根结点，然后将根结点保存，再去遍历左子树，当左子树遍历完成后，取出根结点，利用根结点获得右子树，再去遍历右子树，从而得到前序遍历的结果。

迭代遍历从根结点到树的最左侧结点，依次入栈每个访问过的结点，当最左侧结点访问后，按照后进先出的顺序将栈中的结点出栈，这样就能根据出栈的结点找到最左侧子树的根节点，根据根结点，获取右子树，这时右子树也是一棵树，首先访问这个子树的根节点，然后入栈，入栈后再访问这个子树的左子树，循环这个过程，得到最终的结果。

实现：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<TreeNode *> stk;
    TreeNode *tempNode = root;
    //只要栈不为空或者tempNode不为空，就表示还有没有处理完的结点
    while(!stk.empty() || tempNode){
    	//向左子树的最深处遍历，同时将每个结点入栈（作为对应左子树的根结点），由于是先序遍历，同时将结果保存
        while(tempNode){     
            result.push_back(tempNode->val);
            stk.push(tempNode);
            tempNode = tempNode->left;
        }
        //找到当前栈顶元素的右子树，同时删除该栈顶元素（这时栈顶里的元素已经被遍历过了，只是用来找到右子树）
        tempNode = stk.top();
        stk.pop();
        tempNode = tempNode->right;
    }
    return result;
}

复杂度分析：

• 时间复杂度：$O(n)$，每个结点被遍历一次
• 空间复杂度：$O(n)$，当到达二叉树的最深处时，栈中保存的元素个数最多，所以空间复杂度的平均情况为 $O(\log n)$，最坏是在树呈链状时，为 $O(n)$。

3. DFS迭代的改进

通过上面可以看出，迭代实现的最终目的是当遍历完左子树进行回溯时，要找到双亲结点的右子树，在上面的实现中，我们每次将根节点入栈，然后根据根结点再找到右子树。

其实我们在入栈时，已经遍历过根结点了，所以我们可以改进以上过程，将右子树的根结点入栈，这样每次出栈的结点就是下次需要访问的结点了。

实现：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> result;
    if(!root){
        return result;
    }

    stack<TreeNode *> stk;
    TreeNode *tempNode;
    stk.push(root);
    //只要栈不为空就表示还有没有处理完的结点
    while(!stk.empty()){
        tempNode = stk.top();
        stk.pop();
        result.push_back(tempNode->val);
        if(tempNode->right){          //右结点入栈
            stk.push(tempNode->right);
        }
        if(tempNode->left){          //左结点入栈
            stk.push(tempNode->left);
        }
    }
    return result;
}

复杂度分析：

• 时间复杂度：$O(n)$，每个结点被遍历一次
• 空间复杂度：$O(n)$，当到达二叉树的最深处时，栈中保存的元素个数最多，所以空间复杂度的平均情况为 $O(\log n)$，最坏是在树呈链状时，为 $O(n)$。

4. Morris 遍历

该遍历可以在线性时间内，只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

其主要思想是利用树的空闲指针，记录当前结点被访问过后，下一个应该访问的结点应该从哪开始，从而节省遍历时的空间复杂度。

利用该方法进行前序遍历的步骤如下：

1. 首先令当前结点 $root$ 指向根结点

2. 如果当前结点的左指针为空，将该结点加入结果中，并让 root 指向当前结点的右孩子（根据前序遍历的定义，应该先访问根结点，当左子树为空时，应该访问右子树）

3. 当前结点的左指针不为空（这时我们一定会遍历完左子树后再遍历右子树，如果要对左子树遍历，那么我们就要找到一个方法，通过该方法我们可以在遍历完左子树后找到右子树，在上面的方法中我们通过栈来确定遍历完左子树后右子树的位置，这里我们就要换一种方法：前序遍历中，左子树最后一个访问的元素一定是左子树最右侧的结点，所以我们可以通过不断找 root->left 的最右侧结点 predecessor，并让这个 predecessor 结点的右指针指向当前 root 结点，那么按照前序遍历到左子树最后一个结点 predecessor 时，通过 predecessor 的 right指针就能找到根结点，那么再取根结点的右子树继续遍历就可以了），找到当前结点的前驱结点 predecessor：

   • 如果前驱结点 predecessor 的右结点为空（表示左子树还没有遍历，本次访问到 predecessor 是在寻找前驱结点），①将 predecessor 的右指针指向 root 结点（这样遍历完左子树时，可以通过左子树的最后一个结点 predecessor 找到根结点，再通过根结点找到要遍历的右子树）。②再将 root 结点加入结果，③将 root 指向 root 的左节点（将当前指针移动到左子树进行遍历）。
   • 如果前驱结点 predecessor 的右结点不为空（表示左子树已经遍历完成了，本次访问到 predecessor 是第二次访问，是在执行步骤2之后回到根结点，再寻找根结点的前驱结点时访问到的），这时①将 predecessor 的右指针置空（恢复为原来的状态）。②将 root 结点指向右子结点（开始遍历右子树）。

4. 循环执行步骤 2 和步骤 3，直到遍历结束。

代码：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> result;

    TreeNode *predecessor;
    while(root != nullptr){
        if(root->left == nullptr){
            //当左子树为空时，将该结点加入结果数组，并将root移动到右子树，前序遍历右子树
            result.push_back(root->val);
            root = root->right;
        }else{  
            //当左子树不为空时，先找到前驱结点
            //获取右子树
            predecessor = root->left;

            //从右子树向右查找，找到最右侧的结点就是根节点的前驱结点（这时前驱结点的右指针为空或者指向根结点）
            while(predecessor->right && predecessor->right != root){
                predecessor = predecessor->right;
            }

            if(predecessor->right == nullptr){
                //如果前驱结点的右指针为空，说明是在寻找前驱结点，这时需要：
                //1. 将前驱结点的右指针指向根结点（方便遍历完右子树后回到根结点）
                //2. 将根结点加入结果
                //3. 将root指向左孩子，开始遍历左子树
                predecessor->right = root;
                result.push_back(root->val);
                root = root->left;
            }else{
                //如果前驱结点的右指针不为空，说明左子树已经遍历完成了，这时需要：
                //1. 将前驱结点的右指针置空（恢复原来的二叉树）
                //2. 将root指向右孩子，开始遍历右子树
                predecessor->right = nullptr;
                root = root->right;
            }
        }
    }
    return result;
}

复杂度分析：

• 时间复杂度：$O(n)$，没有左子树的结点被访问一次，有左子树的结点被访问两次
• 空间复杂度：$O(1)$，只有操作时的指针，没有额外的空间

5. 颜色标记法

这种方法是在题解中发现的，通过这种方式，可以将三种遍历方式的代码统一，而且更好理解。

主要思想：

• 使用颜色标记结点的状态，新结点为白色，已经访问的结点为灰色（下面代码中用 0 表示白色，1 表示灰色）
• 第一步将根节点标记为白色结点入栈，进入循环后将栈顶元素出栈
• 如果遇到的结点为白色，将其标记为灰色，然后根据不同的遍历顺序，将自身、左节点和右节点入栈（第一次入栈的元素都标记为白色，表示没有访问过）。对于前序遍历，由于栈是先进先出的结构，并且我们想要先访问左结点，再访问右结点，我们就需要根据输出的顺序反向入栈，所以对于前序遍历，入栈的顺序为 ①右结点，②左节点，③根节点。
• 如果遇到的是灰色结点，将结点的值输出（其实每次出栈，对应的都是判断是否已经将其左右结点入栈，如果左右结点已经入栈，出栈元素的颜色为灰色，表示可以加入结果了）

代码：

vector<int> preorderTraversal(TreeNode* root) {
    vector<int> result;
    if(root == nullptr){
        return result;
    }
    //创建保存所有元素的栈
    stack<pair<TreeNode *, int>> stk;

    //将根结点标记为白色入栈
    stk.push(make_pair(root, 0));

    pair<TreeNode *, int> tempPair;
    while(!stk.empty()){
        tempPair = stk.top();
        stk.pop();
        if(tempPair.second == 0){
            //如果栈顶元素为白色，说明还没有访问过，这时根据遍历的顺序将左右子树和自己入栈，保证出栈时的顺序等于前序遍历
            if(tempPair.first->right) stk.push(make_pair(tempPair.first->right, 0));
            if(tempPair.first->left) stk.push(make_pair(tempPair.first->left, 0));
            //标记为灰色表示其子结点已经加入了栈，当前结点可以加入结果中了
            stk.push(make_pair(tempPair.first, 1));
        }else{
            result.push_back(tempPair.first->val);
        }
    }
    return result;
}

二、中序遍历

中序遍历的顺序为：

• 中序遍历左子树
• 访问根结点
• 中序遍历右子树

在访问左子树或右子树时，同样按照中序遍历的方式进行。

1. 递归

根据中序遍历的定义和前序遍历的参考，我们应该能够很容易的完成递归的中序遍历，相比于前序遍历，只需要将结点的访问放在遍历完左子树之后即可。

代码：

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> result;
    inorder(root, result);
    return result;
}
void inorder(TreeNode *root, vector<int> &res){
    if(!root){
        return;
    }
    inorder(root->left, res);
    res.push_back(root->val);
    inorder(root->right, res);
}

复杂度分析：

• 时间复杂度：$O(n)$，$n$ 是结点个数，每个结点被访问一次。
• 空间复杂度：$O(n)$，当二叉树为一条链时，递归的堆栈深度深度最大，此时空间复杂度为 $O(n)$。

2. DFS迭代

中序遍历的遍历顺序是先遍历左子树，遍历根结点，最后遍历右子树，所以使用迭代方法的主要思想是使用深度优先搜索一直向左子树的最深处走（走到最左侧的左子树遍历），栈中保存经过的每个结点，当左子树访问完成后，可以从栈中找到左子树对应的根结点，访问完根结点后，也可以通过该根结点获得右子树的位置，从而实现通过栈模拟递归栈。

代码：

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<TreeNode *> stk;
    TreeNode *tempNode = root;
    while(!stk.empty() || tempNode){
        //走到左子树的最深处
        while(tempNode){
            stk.push(tempNode);
            tempNode = tempNode->left;
        }
        //获取栈顶的元素，将该元素加入结果中（因为最左端的结点一定会进入栈后才会跳出上面的循环，所以出栈的一定是最左边的结点）
        tempNode = stk.top();
        stk.pop();
        result.push_back(tempNode->val);
        //遍历右子树
        tempNode = tempNode->right;
    }
    return result;
}

复杂度分析：

• 时间复杂度：$O(n)$，每个结点访问一次
• 空间复杂度：$O(n)$，最坏情况是二叉树形成一个链，二叉树的深度决定空间复杂度

3. Morris 遍历

Morris 遍历算法的步骤如下：

1. 如果当前结点 root 没有左孩子，先将 root 的值加入结果（表示左子树已经遍历完成了，所以将根节点加入结果），再将 root 指针指向右节点（开始遍历右子树）
2. 如果有左孩子，需要先找到当前结点的前驱结点 predecessor，并对 predecessor 进行判断：
   1. 如果 predecessor 的右指针为空，表示还没有建立 root 和其前驱结点 predecessor 的链接，这时 ①令predecessor->right = root （用于遍历完左子树后，从左子树的最后一个结点返回根结点），② 让root = root->left（开始遍历左子树）
   2. 如果 predecessor 的右指针不为空，表示 predecessor->right == root（这时当前指针是通过第一步predecessor没有左孩子时移动到 root的），是遍历完左子树回到的根结点，这时①令predecessor->right = nullptr（将二叉树恢复为原来的样子），②将根节点加入结果（遍历完左子树应该遍历根结点），③令root = root->right（开始遍历右子树）
3. 重复步骤一和步骤二

代码：

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<TreeNode *> stk;
    TreeNode *predecessor;

    while(root){
        if(root->left == nullptr){
            result.push_back(root->val);
            root = root->right;
        }else{
            predecessor = root->left;
            while(predecessor->right != nullptr && predecessor->right != root){
                stk.push(predecessor);
                predecessor = predecessor->right;
            }
            if(predecessor->right == nullptr){
                //如果predecessor->right == nullptr，说明是在寻找前驱结点，这时将前驱结点的右指针指向根结点
                predecessor->right = root;
                root = root->left;
            }else{
                //如果predecessor->right == root，说明这时左子树已经遍历完成了，先将根节点加入结果，再遍历右子树
                predecessor->right = nullptr;
                result.push_back(root->val);
                root = root->right;
            }
        }
    }
    return result;
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$，只有常数个额外空间

4. 颜色标记法

相对于前序遍历，中序遍历的颜色标记法只是让结点的入栈顺序不同，因为中序遍历是按照左、根、右得到结果的，所以我们修改未访问过的结点入栈顺序为右、根、左即可。

代码：

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<pair<TreeNode *, int>> stk;
    if(root == nullptr){
        return result;
    }
    stk.push(make_pair(root, 0));//标记为白色

    pair<TreeNode*, int> tempNode;

    while(!stk.empty()){
        tempNode = stk.top();
        stk.pop();
        if(tempNode.second == 0){
            if(tempNode.first->right) stk.push(make_pair(tempNode.first->right, 0));
            stk.push(make_pair(tempNode.first,1));
            if(tempNode.first->left) stk.push(make_pair(tempNode.first->left, 0));
        }else{
            result.push_back(tempNode.first->val);
        }
    }

    return result;
}

三、后序遍历

中序遍历的顺序为：

• 后序遍历左子树
• 后序遍历右子树
• 访问根结点

在访问左子树或右子树时，同样按照后序遍历的方式进行。

1. 递归

根据后序遍历的定义，可以用如下代码实现：

void postorder(TreeNode *root, vector<int> &res) {
    if (root == nullptr) {
        return;
    }
    postorder(root->left, res);
    postorder(root->right, res);
    res.push_back(root->val);
}

vector<int> postorderTraversal(TreeNode *root) {
    vector<int> res;
    postorder(root, res);
    return res;
}

复杂度分析：

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$，递归时需要通过栈保存信息，树的深度决定栈的最大开销，平均情况为 $O(\log n)$，最坏情况为 $O(n)$

2. 迭代

可以使用迭代的方式，将递归使用的栈模拟出来，实现递归的功能。

类比于前序和中序遍历的迭代方法，我们可以使用深度优先搜索的方式，利用栈模拟递归的本质是从栈中找到下一个要访问的结点，对于后序遍历，我们要先访问左子树，再访问右子树，最后访问根结点。

我们可以将根节点入栈，然后遍历左子树，当遍历完左子树后，将根节点从栈中弹出，这时我们要先判断右子树是否已经遍历完成，这时就需要额外指针的辅助了（不能简单的直接将根节点入栈后，遍历完右子树再取出根结点，这样就不能判断是从左子树遍历结束还是右子树遍历结束取出的根节点），设置一个 prev 指针，这个指针指向上一个遍历的结点，因为对于后序遍历，一定是遍历完右子树才遍历根结点，当回到根节点时，看一下 prev 指针是否指向右子树的根节点，就能判断是从左子树还是右子树回到根节点的，从而实现整体后序遍历。

代码：

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> result;
    stack<TreeNode *> stk;
    if(root == nullptr){
        return result;
    }
    TreeNode *prev = nullptr;
    TreeNode *tempNode = root;

    while(!stk.empty() || tempNode != nullptr){
        //深度优先搜索先走到二叉树的最左边
        while(tempNode != nullptr){
            stk.push(tempNode);
            tempNode = tempNode->left;
        }
        tempNode = stk.top();
        
        //判断当前结点的右子树是否为空
        if(tempNode->right == nullptr || tempNode->right == prev){
            //如果右子树为空，或者右子树等于上一个访问的结点（一定是遍历完右子树回到根节点的）
            result.push_back(tempNode->val);
            prev = tempNode;      //令 prev 指向上一个访问的结点
            tempNode = nullptr;   //当前结点一定是某个子树的根节点，这个结点访问后就表示这个子树已经遍历完成了，所以令tempNode = nullptr，这样上面就会取出栈中的下一个子树的根结点进行遍历
            stk.pop();
        }else{
            //如果右子树不为空，且右子树没有访问过，这时将遍历的指针移动到右子树，开始遍历右子树
            tempNode = tempNode->right;
        }
    }
    return result;

}

复杂度分析:

• 时间复杂度：$O(n)$，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
• 空间复杂度：$O(n)$，为迭代过程中显式栈的开销，平均情况下为 $O(\log n)$，最坏情况下树呈现链状，为 $O(n)$。

3. Morris遍历

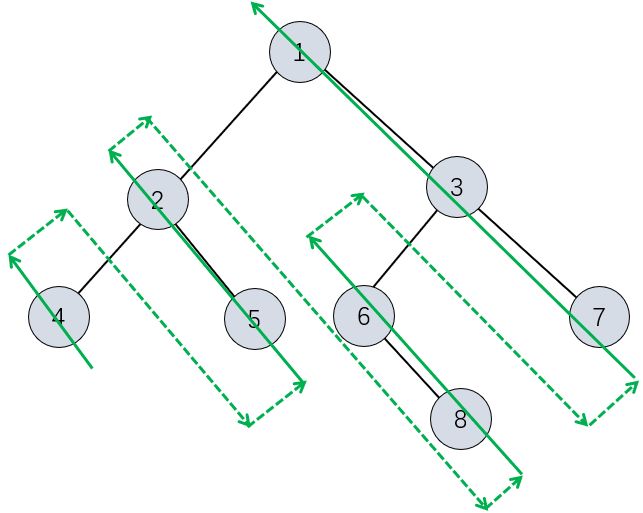
Morris 遍历实现后序遍历和前序与中序中的实现方式有一些不同，主要是在元素的输出方式有差异。主要思路和原来相同，建立左子树最右侧结点和根结点的链接，之后当运行到某个根结点的前驱结点的右指针等于自身时，表示第二次访问到根结点，这时应该倒序输出当前结点左结点到前驱结点这条路径上的前驱结点。

Morris实现的后序遍历实际等价于首先遍历当前结点的所有左子树，对每个子树，都是先访问最左端的结点，再访问右侧结点，然后访问根结点，由于先访问右结点再访问根结点不太方便，通过访问过根节点后再访问右结点，之后逆序，得到正确的顺序，可以用下图表示：

代码：

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> result;
    TreeNode *predecessor;
    TreeNode *currentNode = root;
    TreeNode *tempNode;
    int nodeNum = 0;
    while(currentNode){
        if(currentNode->left == nullptr){
            currentNode = currentNode->right;
        }else{
            //找到当前结点的前驱结点
            predecessor = currentNode->left;
            while(predecessor->right != nullptr && predecessor->right != currentNode){
                predecessor = predecessor->right;
            }
            //对前驱结点的右指针状态进行判断
            if(predecessor->right == nullptr){
                //如果右指针为空，将右指针指向当前结点
                predecessor->right = currentNode;
                currentNode = currentNode->left;
            }else{
                //如果右指针指向当前结点，这时先将右指针置空
                predecessor->right = nullptr; //将二叉树恢复为原来状态
                
                //将当前结点左孩子到前驱结点的所有结点加入结果后，逆序，得到后序遍历的顺序
                tempNode = currentNode->left;
                while(tempNode){
                    result.push_back(tempNode->val);
                    nodeNum++;
                    tempNode = tempNode->right;
                }
                reverse(result.end() - nodeNum, result.end());
                nodeNum = 0;

                //将当前结点指向右指针
                currentNode = currentNode->right;
            }
        }
    }
    //将根结点到最右方的结点值依次加入结果
    //根结点不是其他结点的左子树，所以要最后单独处理
    tempNode = root;
    while(tempNode){
        result.push_back(tempNode->val);
        nodeNum++;
        tempNode = tempNode->right;
    }
    reverse(result.end() - nodeNum, result.end());
    return result;
}

复杂度分析：

• 时间复杂度：O(n)O(n)，其中 nn 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
• 空间复杂度：O(1)O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

4. 颜色标记法

对于后序遍历，颜色标记法只需要按照左、右、后相反的顺序，将其中的结点入栈即可，代码如下：

vector<int> postorderTraversal(TreeNode* root) {
    vector<int> result;
    if(root == nullptr){
        return result;
    }
    stack<pair<TreeNode *, int>> stk;
    pair<TreeNode *, int> tempNode;
    stk.push(make_pair(root, 0)); //根结点入栈，标记为白色

    while(!stk.empty()){
        tempNode = stk.top();
        stk.pop();
        if(tempNode.second == 0){
            stk.push(make_pair(tempNode.first, 1));
            if(tempNode.first->right) stk.push(make_pair(tempNode.first->right, 0));
            if(tempNode.first->left) stk.push(make_pair(tempNode.first->left, 0));
        }else{
            result.push_back(tempNode.first->val);
        }
    }
    return result;
}

---

参考链接：

• 前序遍历官方题解
• 中序遍历官方题解
• 后序遍历官方题解
• 颜色标记法参考题解