位图&布隆过滤器

---

位图&布隆过滤器

1. 位图

给定40亿个不重复的正整数，如何快速判断一个数组是否在这40亿个数中。解决方案：

1. 直接遍历，时间复杂度$O(n)$
2. 排序后二分查找，时间复杂度$O(nlogn)$

以上方法使能解决，但如果考虑到空间复杂度40亿个正整数需要将近15G的内存，如果内存不存就无法做到。那么此时就可以引入位图。

1.1位图概念

位图是一种数据结构，它通过每一个比特位来存放某一种状态，适合存储海量的数据，整数，数据无重复的场景，一般是用来判断某一个数据是否存在的。

比如上面那个例子，一个整数就是4个字节，$4\ast 4000000000/1024/1024/1024$，大约是占用了15G的内存，而如果使用位图存储这40亿个正整数，$4000000000/32\ast 4/1024/1024$,大约就是480M的内存。这个内存占用直接降低了一个数量级。

1.2位图原理

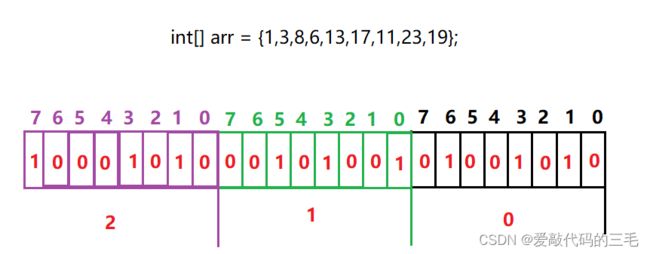
一个数据是否存也就两种状态，在或者不在，通过二进制的0和1就可以表示，位图存储数据就是通过比特位来判断数据是否在位图中存在，0表示不存在1表示存在。通过公式计算出一个数据在哪个比特位。下图分别表示3个数组下标，每个下标都是1个字节(Byte)。

• 计算数组下标公式：数值/8​
• 计算算在数数据在某个下标某一个比特位上：数值%8​
• 加设要把3存入位图，3/8得到数组下标为0，3%8得到比特位为3，所以元素3要存放到下标为0位置的第3个比特位处。

1.3位图实现

位图实现主要的3个功能：

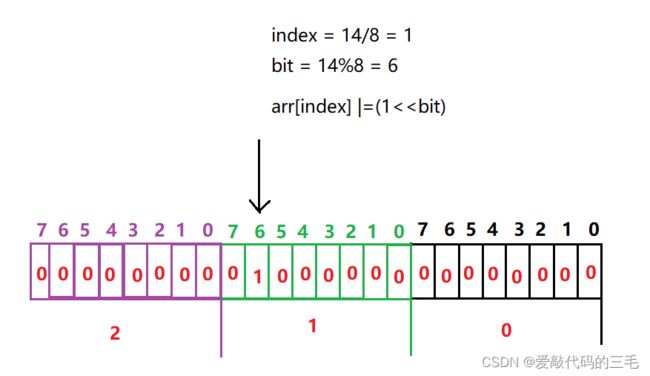
• 设置元素到位图中，通过按位与运算给对应比特位设置为1，假设存14到位图中

  

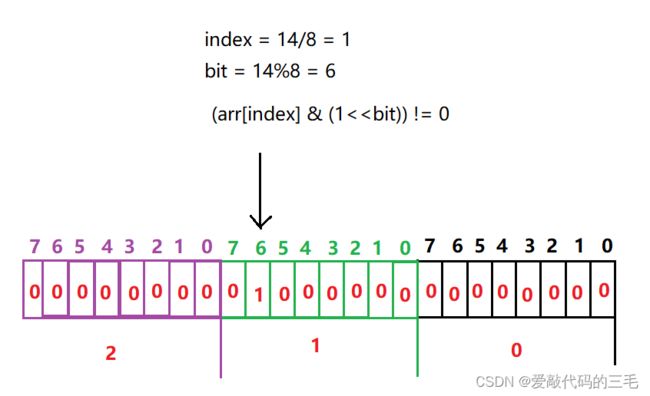
• 查询一个元素是否在位图中，以同样的方法进行按位与运算判断对应位置是否为1，如图下标为1的位置的第6个比特位是否为1

  

• 把一个元素从位图中移除，通过按位取反再进行按位与运算来移除对应标注的二进制位，假设要移除的是19

  

import java.util.Arrays;

public class MyBitSet {
    private byte[] elem;
    public MyBitSet() {
        this.elem = new byte[8];
    }
    public MyBitSet(int nBits) {
        this.elem = new byte[nBits];
    }

    /**
     * 添加 bitIndex元素到位图中
     * @param bitIndex
     */
    public void set(int bitIndex) {
        if (bitIndex < 0) {
            throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
        }
        // 计算数组下标
        int index = bitIndex/8;
        if (index >= elem.length) {
            // 扩容
            elem = Arrays.copyOf(elem,index+1);
        }
        // 计算二进制位
        int bit = bitIndex%8;
        elem[index] |= (1<<bit);
    }

    /**
     * 判断 bitIndex元素在位图中是否存在
     * @param bitIndex
     * @return
     */
    public boolean get(int bitIndex) {
        if (bitIndex < 0) {
            throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
        }
        // 计算数组下标
        int index = bitIndex/8;
        if (index >= elem.length) {
           return false;
        }
        // 计算二进制位
        int bit = bitIndex%8;
        if ((elem[index]&(1<<bit)) != 0) {
            return true;
        }
        return false;
    }

    public void remove(int bitIndex) {
        if (bitIndex < 0) {
            throw new IndexOutOfBoundsException("bitIndex < 0: " + bitIndex);
        }
        // 计算数组下标
        int index = bitIndex/8;
        if (index >= elem.length) {
            return;
        }
        // 计算二进制位
        int bit = bitIndex%8;

        elem[index] &= (~(1<<bit));
        
    }
}

1.4位图排序

可以利用位图来进行简单的排序，也就是从第一个比特位开始判断是否有元素，有元素以存入的方式进行取出。

public void sort(int[] elem) {
    for (int i = 0; i < elem.length; i++) {
        for (int j = 0; j < 8; j++) {
            if (((elem[i]>>>j)&1) == 1) {
                System.out.print(j+(i*8)+" ");
            }
        }
    }
}

2. 布隆过滤器

2.1 引入布隆过滤器

在编程时，我们经常要判断一个元素是否在一个集合中出现，第一时间想到的应该是哈希表，它的优点就是增删改查快速又准确，缺点也是有的那就是存在着空间的浪费，当数据量非常大时就凸显出来了，数据量非常大时哈希表会存在非常多的key，同时发送大量的哈希冲突，使用链地址方法来解决，从而产生大量的节点占用大量的空间，如果使用线性探测就会降低查询效率。假设要判断一个email是否在几十亿的email中出现。

如果用哈希表存储一亿个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个
email 地址对应成一个八字节的信息指纹,然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有
50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此
存贮几十亿个邮件地址可能需要上百 GB 的内存。

方法：

1. 是哈希表存储用户记录，缺点：占用大量空间
2. 使用用位图存储用户记录?无法实现，因为位图只能处理整形。
3. 将哈希和位图进行结合，也就是布隆过滤器

2.2 概念

布隆过滤器是一种比较巧妙的概率形数据结果，其特点是高效地插入和查询，可以用来告诉你“某样东西一定不存在或者可能存在”，布隆过滤器使用多个哈希函数，将一个数据映射到位图结构中。从而提升查询效率，也可以节省大量的内存空间。

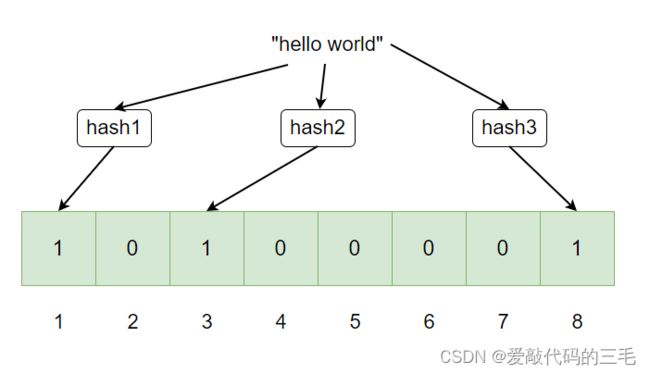
2.3 布隆过滤器插入

假设布隆过滤器中有3个hash函数，要往布隆过滤器中插入"hello world"，通过3个不同的hash函数得到不同的hash值，然后再把hash值设置在位图的3个比特位中。

2.4 布隆过滤器的查找

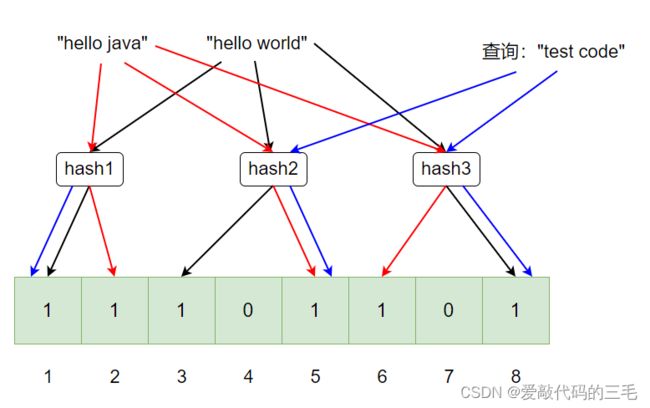
布隆过滤器的基本思想是将一个元素通过多个hash函数得到hash值后，设置到位图的不同比特位中。查询通过同样的hash函数去判断位图对应的比特位是否为1，只要一个比特位不唯一，那么这个元素就一定不存在，相反查询的比特位全部唯一也只是可能存在。因为通过hash函数必定会发生hash冲突，可能会出现下图这种情况：

"hello java"和"hello world"两个元素已经存放到布隆过滤器中，此时"test code"未存放到布隆过滤器中，此时去查询"test code"中查询的时候恰巧hash到的位图中的位置，都被"hello"和“hello world“标记过了，此时就返回"test code"这个元素存在吗？显然是不存在的。所以布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可能存在，因为有些哈希函数存在一定的误判

2.5 布隆过滤器模拟实现

通过参考HashMap的哈希函数再随缘加上一些随机因子，使用了3个哈希函数对元素进行哈希并设置到位图当中。

/**
 * 布隆过滤器模拟实现
 * @param 
 */
public class BloomFilter<E> {
    static class RandomHash {
        // 容量
        int size;
        // 随机种子
        int seed;

        public RandomHash(int size, int seed) {
            this.size = size;
            this.seed = seed;
        }
        /**
         * 计算机哈希值
         * @param key 元素
         * @return
         */
        private int hash(Object key) {
            int h;
            // (n-1)&hash == hash%n
            return (key == null) ? 0 : (seed*(size-1))&(h = key.hashCode()) ^ (h >>> 16);
        }
    }
    // 位图默认容量，参照hashmap，方便hash函数计算
    private static final int DEFAULT_SIZE = 1 << 21;
    // 随机因子
    private static final int[] RANDOM_FACTOR = {3,7,11};
    // 布隆过滤器元素个数
    private int size;
    private BitSet bitSet;
    // 哈希函数
    private RandomHash[] randomHashes;

    public BloomFilter() {
        bitSet = new BitSet(DEFAULT_SIZE);
        randomHashes = new RandomHash[RANDOM_FACTOR.length];
        for (int i = 0; i < randomHashes.length; i++) {
            randomHashes[i] = new RandomHash(DEFAULT_SIZE,RANDOM_FACTOR[i]);
        }
    }

    /**
     * 添加元素到布隆过滤器中
     * @param key
     */
    public void add(E key) {
        for (int i = 0; i < randomHashes.length; i++) {
            int hash = randomHashes[i].hash(key);
            bitSet.set(hash);
        }

    }

    /**
     * 判断元素是否可能存在布隆过滤中
     * @param key
     * @return
     */
    public boolean contains(E key) {
        for (int i = 0; i < randomHashes.length; i++) {
            int hash = randomHashes[i].hash(key);
            if (!bitSet.get(hash)) {
                return false;
            }
        }
        return true;
    }




    public static void main(String[] args) {
        BloomFilter<Integer> bloomFilter = new BloomFilter<>();
        for (int i = 1000; i < 2000; i++) {
            bloomFilter.add(i);
        }
        int count = 0;
        for (int i = 1000; i <= 70000000; i++) {
            if (bloomFilter.contains(i)) {
                count++;
            }
        }
        System.out.println(count);
    }
}

2.6 布隆过滤器的删除

布隆过滤器是无法直接删除的，和查询类似会存在误删除。因为存储元素必定会存在哈希冲突的，如果删除一个元素则会把对应的比特位标记为0，一旦有其它元素也哈希到了这个位置，那么也会就会影响到其它元素，因为布隆过滤器查询的时候只要有一个比特位为0，就认为这个元素一定不存在。所以布隆过滤器不能直接删除。

如果想实现布隆过滤器的删除：可以采用加减标记的方式，一起添加元素是将hash过后的比特位标记成1，可以改成给位图对应的位置+1，删除就给对应的位图下标-1，但这样做需要更大的空间，而且+1和-1存溢出问题。

2.7 布隆过滤器优缺点

优点：

1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无关

2. 哈希函数相互之间没有关系，方便硬件并行运算

3. 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势

4. 在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势

5. 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能

6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

缺点：

1. 无法确认元素是否真正在布隆过滤器中，误判问题
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素
4. 如果采用计数方式删除，可能会存在计数回绕问题

2.8 布隆过滤器使用场景

1. 网络爬虫：在网络爬取数据的过程中，可以使用布隆过滤器来过滤掉已经爬取过的网页链接，避免重复爬取相同的内容。
2. 缓存服务：在缓存中使用布隆过滤器可以快速判断某个数据是否存在于缓存中，如果不存在就从数据库或其他存储中获取，并将其添加到缓存中，减轻数据库或存储系统的负载压力。
3. 反垃圾邮件系统：布隆过滤器可以用于过滤垃圾邮件。将已知的垃圾邮件发送者的信息加入到布隆过滤器中，当新邮件到达时，可以快速判断其发件人是否为已知的垃圾邮件发送者，从而减少用户收到垃圾邮件的数量。
4. 分布式系统：在分布式系统中，布隆过滤器可以用于去重操作，避免重复处理相同的数据和请求。各个节点可以共享一个布隆过滤器，快速判断某个数据是否已经被处理过。

总的来说，布隆过滤器适用于需要快速判断某个元素是否存在的场景，并且能够容忍一定的错误率

3. 海量数据问题

问题1

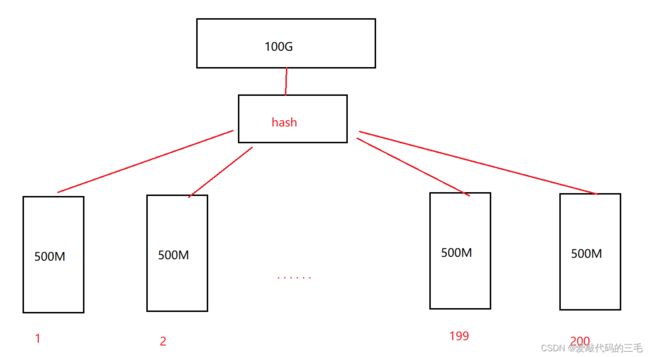
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？ 与上题条件相同，如何找到top K的IP？

该问题可以使用哈希切割，新建200个文件，每个文件存储500M的数据，从文件中开始读取100G的数据，对读取到的ip地址进行哈希后，再对hash值%200存放到对应的文件中。最后依次读取200个文件，记录ip出现的次数即可。同理，如果是TOP k问题，也是如此。

3.2 问题2

给定100亿个整数，设计算法找到只出现一次的整数？ 100亿个整数大概是$10000000000\ast 4/1024/1024/1024$,40G的大小，显然内存是存不下的。

解法1：

同理可以使用Hash切割，将这100亿个数hash到不同文件上，再遍历文件即可。

解法2：

100亿个整数存放到一个位图大概是$10000000000/32\ast 4/1024/1024/1024$，大概就是1个G的内存。

使用两个位图，可以表示数组出现了多少次，1次、2次或者3次。

比如说：

• 位图1的第0个比特位为0位图2第0个比特位为1，就表示对应位置的数出现的次数为1
• 位图1的第0个比特位为1位图2第0个比特位为0，就表示对应位置的数出现的次数为2
• 位图1的第0个比特位为1位图2第0个比特位为1，就表示对应位置的数出现了3次

解法3：使用一个位图

和解法2类似，采用类似二进制的表示出现的次数，只不过使用一个位图要两个比特位才能表示一个数字。

原本的公式是：下标：$index=key/8$，比特位：$bit=key$%$8$

采用两个比特位标识一个数字：下标$index=key/4$，比特位：$bit=key$%$4\ast 2$

问题3

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

解法1：

使用hash切割，把两个文件先分别分割成200个文件，也就是400个文件，读取文件1分割的问题件的同时去读取文件2对应分割的文件，由于hash函数是一致的，相同的数字会被放到同一个文件中，比如说文件1分割出来的文件1.1和文件2分割出来的2.1，使用的是同一个哈希函数，只要在两个文件里找相同的数字即可。

解法2：

使用位图把第一个文件中的数据存到位图中，再遍历第二个文件中的数字看看是否在位图中存在，存在就是交集。

问题4

1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

解法1:

hash切割，切割到多个文件，一个一个文件统计

解法2：

使用两个位图，只要两个位图没有同时为1，那就是没有超过两次

问题5

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和
近似算法

精确算法：两个文件分别哈希切割成多个文件，分两组。在依次对应读取两个文件判断是否有相同的存在。

近似算法：把一个文件的数据读取到布隆过滤器，再读取第二个问题，判断是否存在，显然会存在误判。

---