信息安全：使用程序编写基于密钥的加密方式

前言

信息安全是计算机科学的一个重要分支，它涉及到保护信息的机密性、完整性和可用性。信息加密是信息安全的一种常用手段，它通过使用一些数学算法和密钥，将明文转换为不易被破解的密文，从而防止未经授权的访问和篡改。本实验的目的是让学生了解基于密钥的加密方式的原理和实现方法，使用程序编写一个简单的加密和解密功能，并测试其效果。本实验分为两个部分：第一部分是理论学习，介绍基于密钥的加密方式的分类和特点，以及常见的加密算法；第二部分是实践操作，使用C语言编写一个基于对称密钥的加密和解密程序，并对不同长度的明文进行加密和解密，观察其运行时间和结果。

RSA算法

RSA算法是一种非对称加密算法，与对称加密算法不同的是,RSA算法有两个不同的密钥,一个是公钥,一个是私钥。
RSA公开密钥密码体制是一种使用不同的加密密钥与解密密钥，“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制 。
在公开密钥密码体制中，加密密钥（即公开密钥）PK是公开信息，而解密密钥（即秘密密钥）SK是需要保密的。加密算法E和解密算法D也都是公开的。虽然解密密钥SK是由公开密钥PK决定的，但却不能根据PK计算出SK 。
正是基于这种理论，1978年出现了著名的RSA算法，它通常是先生成一对RSA密钥，其中之一是保密密钥，由用户保存；另一个为公开密钥，可对外公开，甚至可在网络服务器中注册。为提高保密强度，RSA密钥至少为500位长。这就使加密的计算量很大。为减少计算量，在传送信息时，常采用传统加密方法与公开密钥加密方法相结合的方式，即信息采用改进的DES或IDEA对话密钥加密，然后使用RSA密钥加密对话密钥和信息摘要。对方收到信息后，用不同的密钥解密并可核对信息摘要 。
RSA是被研究得最广泛的公钥算法，从提出后经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。1983年麻省理工学院在美国为RSA算法申请了专利 。
RSA允许选择公钥的大小。512位的密钥被视为不安全的；768位的密钥不用担心受到除了国家安全管理（NSA）外的其他事物的危害；RSA在一些主要产品内部都有嵌入，像 Windows、网景 Navigator、 Quicken和 Lotus Notes 。
由于RSA算法1024位密钥面临严重的安全威胁,为保障电子认证服务安全应用,2016年12月5日,上海市密码管理局在其官方网站上发布公告,称从2017年1月1日起停止提供RSA算法1024位密钥对服务,并配合电子认证服务机构和应用单位做好应对措施,确保平稳过渡。

代码实现

#include
#include
#include 
 
const int max=2e4;
int size;
int miwen[max];//为加密后的数字密文
char mingwen[max]; 
 
//判断两个数是否互为素数  eg:p和q e和 t 
bool gcd(int p,int q)
{
	int m,n;
	if(q<p)
	{
		m=p;  p=q;  q=m;  //将p换成p和q之间那个小的数 
		m=q%p;  n=q/p;  //辗转相除法求两个数的最大公因数 
	}
	while(m!=0)
	{
		q=p; p=m;  //将p换成p和q之间那个小的数
		m=q%p;  n=q/p;		
	} 
	if(m==0&&n==q)
	{
		printf("符合条件！\n");
			return true;
	}
	else{
		printf("不符合条件！请重新输入：\n");
	    	return false;
	}
} 
//判断输入的p和q是不是素数 
bool sushu(int s){
	for(int i=2;i<s;i++){
		if(s%i==0) 
		return false;
	}
	return true;
}
//求私钥d
int siyao(int e,int t)  //t:欧拉函数 
{
	int d;
	for(d=0;d<t;d++)
	    if(e * d % t==1)
	       return d;
}
//随机生成与 t互质的数e
int getrand(int p,int q)
{
	int t=(p-1)*(q-1);
	while(1)
	{
		int e=rand() % t;
		if(gcd(e,t)==1)
		return e;
	//	if(e<=2)
	//	e=3;
	}
}
void jiami(int e,int n) 
{
	//先将符号明文转换成字母所对应的ascii码。 
	char mingwen[100];    //符号明文 
	printf("请输入明文：\n");
	scanf("%s",mingwen);
	size=strlen(mingwen);
	int ming[strlen(mingwen)];   //定义符号明文 
	for(int i=0;i<strlen(mingwen);i++)
	{
	   ming[i]=mingwen[i];        //将字母转换成对应的ascii码。 
	//printf("%d",mingwen[i]);  //将字母转换成对应的ascii码。可以不输出 
	} 
	int flag=1;    //miwen为加密后的数字密文 
	for(int i=0;i<strlen(mingwen);i++)
	{
	    for(int j=0;j<e;j++)
		{
		    flag=flag*ming[i]%n; 
	    }
	    miwen[i]=flag; 
	    flag=1;
	} 
	printf("加密密文为：\n");
	for(int i=0;i<strlen(mingwen);i++) 
	printf("%d",miwen[i]); 
}
void jiemi(int d,int n)
{
	int de_mingwen[size],flag=1;//解密后得到的数字明文（即ascii码） 
	char de_ming[size];//解密后得到的字符串明文 
	for(int i=0;i<size;i++)
	{
	   for(int j=0;j<d;j++)
	   {
	   	  flag=flag*miwen[i]%n;
	   }
	   de_mingwen[i]=flag; 
	   flag=1;
	} 
	printf("解密后的明文为：\n");
	for(int i=0;i<size;i++)
	{
		de_ming[i]=de_mingwen[i];
		printf("%c",de_ming[i]);
	}
}
int main()
{
	int p,q,e,d,n,t,tep;
	while(1)
	{
		printf("请输入p:",p);
		scanf("%d",&p);
		tep=sushu(p);
		if(tep==0)
		{
			printf("p不是素数，请重新输入p！\n");
		    continue;
		} 
		printf("请输入q:",q);
		scanf("%d",&q);
	    tep=sushu(q);
	    if(tep==0)
		{
		printf("q不是素数，请重新输入q！\n");
		printf("请输入q:",q);
		scanf("%d",&q);
		tep=sushu(q);
		}
		int n=p*q;
		int t=(p-1)*(q-1);
		tep=gcd(p,q);
		if(tep==0)   continue;
		printf("t=(q-1)*(p-1)=%d\n",t);
		e=getrand(p,q);
		printf("公钥(e=%d n=%d)\n",e,n);
		tep=(e,t);
		d=siyao(e,t);
		printf("私钥d=%d",d);
		int a=0;
		while(a!=3)
		{
			printf("\n-------------------------\n");
			printf("1、加密\n");
	        printf("2、解密\n");
	        printf("3、退出");
	        printf("\n-------------------------\n");
	        scanf("%d",&a);
	        getchar();
	        if(a==1)
	        {
	        	jiami(e,n);
	        }
	        else if(a==2)
	        {
	        	printf("请输入密钥：");
		        scanf("%d",&d);2
		        jiemi(d,n);
	        }
	        else 
			     return 0;
		}		
    }
    return 0;
}

设计思路

RSA加密算法的设计思路是基于数论的一些性质，主要有以下几个步骤：

首先，选择两个大的素数p和q，计算它们的乘积n，作为公钥的一部分。n的长度就决定了RSA算法的安全强度。
然后，计算n的欧拉函数φ(n)，即小于n且与n互质的正整数的个数。根据数论的性质，φ(n) = (p-1)(q-1)。
接着，选择一个整数e，使得e与φ(n)互质，即最大公约数为1。e也作为公钥的一部分，用于加密信息。
然后，利用扩展欧几里得算法，求出e对于φ(n)的模反元素d，即满足ed ≡ 1 (mod φ(n))的整数d。d作为私钥的一部分，用于解密信息。
最后，将公钥(e, n)和私钥(d, n)分别保存或发布。加密信息m时，计算c = m^e mod n，得到密文c。解密密文c时，计算m = c^d mod n，得到明文m。
这样，RSA算法就实现了非对称加密和解密的过程，利用了素数分解和模反元素的难度来保证安全性。更多细节和证明可以参考这篇文章link或这篇文章link。

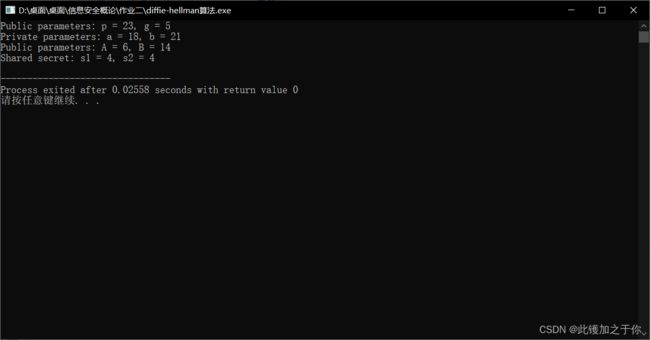
结果示意

Diffie-Hellman算法

Diffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一，它使得通信的双方能在非安全的信道中安全的交换密钥，用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法，之后被应用于安全领域，比如 Https 协议的 TLS(Transport Layer Security) 和 IPsec 协议的 IKE(Internet Key Exchange) 均以 DH 算法作为密钥交换算法。

代码实现

#include 
#include 
#include 

// 定义一个函数，用于计算a的b次方模n的结果
int mod_pow(int a, int b, int n) {
    int res = 1;
    while(b > 0) {
        if(b & 1) { // 如果b的最低位为1，则将res乘以a并取模
            res = (res * a) % n;
        }
        a = (a * a) % n; // 将a平方并取模
        b >>= 1; // 将b右移一位
    }
    return res;
}

// 定义一个函数，用于测试Diffie-Hellman加密算法
void test() {
    // 定义公共参数p和g，这两个参数可以公开
    int p = 23; // 一个大素数
    int g = 5; // 一个小于p的整数
    printf("Public parameters: p = %d, g = %d\n", p, g);

    // 定义私有参数a和b，这两个参数不对外公开
    int a = rand() % p; // A方随机选择一个小于p的整数作为私有参数
    int b = rand() % p; // B方随机选择一个小于p的整数作为私有参数
    printf("Private parameters: a = %d, b = %d\n", a, b);

    // 定义公开参数A和B，这两个参数可以互相交换
    int A = mod_pow(g, a, p); // A方计算g的a次方模p的结果作为公开参数
    int B = mod_pow(g, b, p); // B方计算g的b次方模p的结果作为公开参数
    printf("Public parameters: A = %d, B = %d\n", A, B);

    // 定义共享密钥s，这个结果是相同的
    int s1 = mod_pow(B, a, p); // A方计算B的a次方模p的结果作为共享密钥
    int s2 = mod_pow(A, b, p); // B方计算A的b次方模p的结果作为共享密钥
    printf("Shared secret: s1 = %d, s2 = %d\n", s1, s2);
}

// 主函数，调用测试函数
int main() {
    test();
    return 0;
}

设计思路

Diffie-Hellman密钥交换算法的设计思路是基于以下的想法：

两个通信方，比如说A和B，想要通过一个公开的不安全的信道，协商出一个共享的密钥，用于后续的对称加密通信。
他们首先选择一个大素数p和一个小于p的整数g，作为公共的参数，任何人都可以知道这两个数。
然后，A和B各自随机选择一个小于p的私有数a和b，作为自己的私钥，不对外公开。
接着，A和B分别计算g的a次方模p和g的b次方模p的结果，作为自己的公钥，互相交换这两个数。
最后，A和B利用对方的公钥和自己的私钥，计算出g的ab次方模p或者g的ba次方模p的结果，作为共享的密钥。由于模幂运算的性质，这两个结果是相同的。
这样，A和B就通过两轮信息交换，实现了密钥协商的过程。由于离散对数问题和计算性Diffie-Hellman问题的难度，即使有人知道了p、g、g的a次方模p和g的b次方模p这四个数，也很难推算出a、b或者g的ab次方模p。因此，这个算法可以保证密钥的安全性。更多细节和证明可以参考这篇文章tink或这篇文章tink。

结果示意