多目标平衡黏菌算法(MOEOSMA)求解八个现实世界受约束的工程问题

 

目录

1 受约束的工程问题

1.1 减速器设计问题(Speed reducer design problem)

1.2 弹簧设计问题(Spring design problem)

1.3 静压推力轴承设计问题(Hydrostatic thrust bearing design problem)

 1.4 振动平台设计问题(Vibrating platform design problem)

1.5 汽车侧面碰撞设计问题(Car side impact design problem)

 1.6 水资源管理问题(Water resource management problem) 

1.7 散货船设计问题(Bulk carriers design problem)

1.8 多产品批量工厂问题(Multi‑product batch plant problem)

---

 

        为了测试多目标智能优化算法的潜力，它被应用于八个现实世界的约束工程问题减速器设计、弹簧设计、静压推力轴承设计、振动平台设计、汽车侧面碰撞设计、水资源管理、散货船设计、多产品批处理厂。

1 受约束的工程问

1.1 减速器设计问题(Speed reducer design problem)

       第一个多目标工程设计问题是Kurpati等人研究的减速器设计问题，其目的是将减速器的重量和应力降至最低。该问题包含七个决策变量：齿轮的表面宽度(b)、小齿轮齿数(z)、齿模(m)、轴承之间的第一轴和第二轴的长度(、)，以及第一和第二轴的直径(，)。小齿轮齿数(z)是一个整数，其他变量是连续的。这是一个混合整数问题，其数学模型如下：

减速器问题示意图

1.2 弹簧设计问题(Spring design problem)

       第二个是弹簧设计问题，这个问题的目的是最大限度地减少压力和体积。设计变量是导线直径（d）、平均线圈直径（d）和有效线圈的数量（N）。约束条件包括外径、剪切应力、作用频率和最小缺陷。这个问题是独特的，因为所有的设计变量都有不同的特性。线圈匝数只能取整数，其中导线直径是标准化的，必须从可用直径中选择。线圈的平均直径可以看作是一个连续变量。

弹簧设计问题示意图

 

1.3 静压推力轴承设计问题(Hydrostatic thrust bearing design problem)

       第三，静压推力轴承设计问题的目标是在满足一些约束的同时，最大限度地减少静压推力轴承在运行过程中的功率损失。提供轴向支撑时，静液压止推轴承必须承受规定的载荷。在本研究中，增加了一个目标函数，以最大限度地减少进油口和出油口的压力损失。在这个问题中考虑了四个设计变量：油粘度(), 进油速率（Q）、轴承台阶半径（R）和凹陷半径（）。有七个约束条件与最小承载能力、入口油压要求、油温升高、油膜厚度和一些物理约束条件有关。假设所有变量都是连续的。

静压推力轴承示意图

 1.4 振动平台设计问题(Vibrating platform design problem)

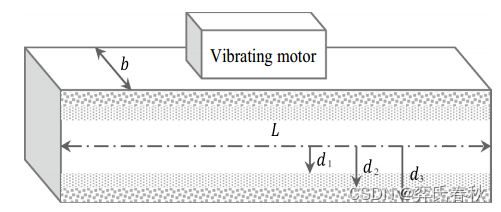
        第四个问题是对Messac提出的振动平台设计问题的修改。它最初被设计为最大化基频的SOP，估计成本是限制因素之一。在这里，问题被修改为包括成本作为第二目标函数，并使问题组合。几何结构和材料在设计过程中是综合的。问题是设计一个用于安装电机的平台。机器的设置被简化为一个由销轴支撑的梁来承受重量。振动扰动从电机施加到梁上，梁的长度为L，宽度为b，并围绕其中间对称。变量和分别定位材料1和2以及材料2和3的接触点。变量定位梁的底部。组合变量是指可以形成梁的每一层的材料的类型。质量密度(), 每种材料类型的杨氏弹性模量（E）和单位体积成本（c），如表1所示。目的是设计夹层梁，以最大限度地减少由于电机干扰引起的梁振动，同时最大限度地降低成本。

振动平台材料特性设计问题

振动平台装置示意图

1.5 汽车侧面碰撞设计问题(Car side impact design problem)

       第五，Jain和Deb 提出了汽车侧面碰撞设计问题。这个问题的目的是最小化汽车的重量，同时最小化乘客所经历的公共力和负责承受冲击载荷的V形支柱的平均速度。这三个目标都是一致的。因此，预计PF将进行三维交易。该问题有十个约束条件，涉及腹部负荷、耻骨力、V形柱速度、肋骨缺陷等的极限值。有十一个设计变量描述了B柱、底座、横梁、门梁、车顶纵梁等的厚度。

 1.6 水资源管理问题(Water resource management problem) 

       第六，水资源管理是城市雨水排放系统的优化规划，最初由Musselman和Talavage提出。这个问题的公式基本上由一个以模拟模型为约束的分层结构线性程序组成。假设排水系统中有三个决策变量，表示局部滞留蓄水量（）、最大处理率（）和最大允许溢流率（）。要优化的目标是排水网络成本（）、储存设施成本（）、处理设施成本（）、预期粮食损失成本（）和预期粮食经济损失（）。该问题有五个目标函数，MOEOSMA和其他比较算法在多目标优化问题上的性能可以评估。

1.7 散货船设计问题(Bulk carriers design problem)

           第七，散货船设计问题是另一个具有挑战性的约束优化问题。该问题的目标是降低运输成本（）、降低船舶重量（）和增加年货运量（）。该问题的决策变量是船舶的长度（L）、梁（B）、深度（D）、吃水深度（T）、速度（）和阻塞系数（）。

1.8 多产品批量工厂问题(Multi‑product batch plant problem)

       第八，多产品批量工厂问题是一个复杂的调度问题。这类问题的早期设计通常是为了降低制造成本和制造周期。它同时考虑了三个目标函数，具有十个决策变量和十个不等式约束。这个混合整数线性规划问题的数学公式详细描述如下。