省选模拟赛Round3Day1 进攻！字符串 序列

 

当我看到题时，心态就已经崩了。。。

 

 

题解

这题其实就是求网格图上的“希望”（有交K连通块计数）

（这里我们把一个面看成一个点，面面之间有公共边则在两个面之间连边）

根据希望那道题的容斥方法（边点容斥）

这种容斥的本质其实就是欧拉图论定理V-E+F=2

欧拉图论定理的适用范围是平面图，而网格图恰好就是平面图

我们先来计算每个点包含它的矩形的数目，再计算出每条边包含它的矩形的数目，再算每个环包含它的矩形的数目

那么最终的答案就等于Σ（点方案数^K）-Σ（边方案数^K）+Σ（环方案数^K）

这样我们就完成了第一步

 

我们现在来考虑如何计算包含一个点的方案

先算出这个点分别作为左上、左下、右上、右下的矩形个数（利用单调队列可以做到总体复杂度O(n^2)）

一个矩形会使点它所覆盖的点的方案数加1

于是我们考虑一种巧妙的差分

 

在计算出当前点的四种矩形个数后

一个1、4处的矩形会使当前点右下方所有点的方案数都加1

一个2、3处的矩形会使当前点右下方所有点的方案数都减1

为什么？

其实我们本应该对1、2、3、4处每一个合法的矩形进行差分

但是由于时间复杂度的限制，我们不能直接这样做

而我们又考虑到：一个矩形，它本身就会被自己的四个顶点分别算到一次

所以我们可以分4次来对它进行差分

至于边、环的方案也可以用类似的方法来做

这样我们就解决了这道题

 

代码：

#include
#include
#include
using namespace std;
#define N 2005
#define LL long long
const int mod=998244353;
char s[N][N];
int h1[N][N],h2[N][N];
int stk[N],top;
LL f[4][N][N];
int ksm(int x,int y)
{
	int ret=1;
	while(y){
		if(y&1)ret=1ll*ret*x%mod;
		y>>=1;x=1ll*x*x%mod;
	}
	return ret;
}
int main()
{
	freopen("attack.in","r",stdin);
	freopen("attack.out","w",stdout);
	int n,m,K,i,j,k;
	scanf("%d%d%d",&n,&m,&K);
	for(i=1;i<=n;i++)scanf("%s",s[i]+1);
	for(i=1;i<=n;i++)for(j=1;j<=m;j++)if(s[i][j]=='1')h1[i][j]=h1[i-1][j]+1;else h1[i][j]=0;
	for(i=n;i>=1;i--)for(j=1;j<=m;j++)if(s[i][j]=='1')h2[i][j]=h2[i+1][j]+1;else h2[i][j]=0;
	for(i=1;i<=n;i++){
		int sum=0;stk[top=1]=0;
		for(j=1;j<=m;j++){
			while(top&&h1[i][stk[top]]>=h1[i][j]){
				sum-=h1[i][stk[top]]*(stk[top]-stk[top-1]);
				top--;
			}
			stk[++top]=j;
			sum+=h1[i][j]*(stk[top]-stk[top-1]);
			f[0][i+1][j+1]+=sum;f[1][i+1][j+1]+=sum;f[2][i+1][j+1]+=sum;f[3][i+1][j+1]+=sum;
		}
	}
	for(i=1;i<=n;i++){
		int sum=0;stk[top=1]=m+1;
		for(j=m;j>=1;j--){
			while(top&&h1[i][stk[top]]>=h1[i][j]){
				sum-=h1[i][stk[top]]*(stk[top-1]-stk[top]);
				top--;
			}
			stk[++top]=j;
			sum+=h1[i][stk[top]]*(stk[top-1]-stk[top]);
			f[0][i+1][j]-=sum;f[1][i+1][j]-=sum;f[2][i+1][j+1]-=sum;f[3][i+1][j+1]-=sum;
		}
	}
	for(i=1;i<=n;i++){
		int sum=0;stk[top=1]=0;
		for(j=1;j<=m;j++){
			while(top&&h2[i][stk[top]]>=h2[i][j]){
				sum-=h2[i][stk[top]]*(stk[top]-stk[top-1]);
				top--;
			}
			stk[++top]=j;
			sum+=h2[i][stk[top]]*(stk[top]-stk[top-1]);
			f[0][i][j+1]-=sum;f[1][i+1][j+1]-=sum;f[2][i][j+1]-=sum;f[3][i+1][j+1]-=sum;
		}
	}
	for(i=1;i<=n;i++){
		int sum=0;stk[top=1]=m+1;
		for(j=m;j>=1;j--){
			while(top&&h2[i][stk[top]]>=h2[i][j]){
				sum-=h2[i][stk[top]]*(stk[top-1]-stk[top]);
				top--;
			}
			stk[++top]=j;
			sum+=h2[i][stk[top]]*(stk[top-1]-stk[top]);
			f[0][i][j]+=sum;f[1][i+1][j]+=sum;f[2][i][j+1]+=sum;f[3][i+1][j+1]+=sum;
		}
	}
	for(k=0;k<4;k++)for(i=1;i<=n;i++)for(j=1;j<=m;j++)
		f[k][i][j]=f[k][i][j]+f[k][i-1][j]+f[k][i][j-1]-f[k][i-1][j-1];
	int ans=0;
	for(i=1;i<=n;i++)for(j=1;j<=m;j++){
		for(k=0;k<4;k++)f[k][i][j]%=mod;
		ans=(1ll*ans+1ll*ksm(f[0][i][j],K)+1ll*mod-1ll*ksm(f[1][i][j],K)+1ll*mod-1ll*ksm(f[2][i][j],K)+1ll*ksm(f[3][i][j],K))%mod;
	}
	printf("%d\n",ans);
}

 

 

 

 

 

 

题解

Trie树预处理+不均匀莫队+删除型回滚+双向链表

这题

本来在考试的时候想到了莫队，但是觉得莫队会被卡爆（比如一个字符串特别长，还被不断地删除加入）

所以就写了可持久化Trie树暴力（竟然只有20分。。。）

没想到可以在分块的时候对字符串的长度加权，做一个不均匀的分块

于是这道题就简单很多了

在普通的Trie树上可以随便统计一个深度满足条件的数的个数

然后利用set来插入删除g[len]，维护两个连续点的差的平方和，再用总的方案数减去这个值就是合法区间的个数

然而O(nsqrt(n)logn)会TLE

我们考虑一种删除很快的数据结构：双向链表

这样，利用类似与回滚莫队的思路，我们先把所有的点都加入莫队，右端点倒序进行莫队

利用双向链表来维护两点差的平方和，这样就只用删除和回退了

双向链表还有一个好处就是：删除的时候不把当前点的指针清零，回退的时候直接按顺序加入就可以了

 

代码：（其实这份代码有个bug：不能直接用权值之和来判断是否存在该前缀，因为权值可能为0！！）

（但是数据太水了，所以过了hhhh）

#include
#include
#include
#include
using namespace std;
inline int gi()
{
	char c;int num=0,flg=1;
	while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
	while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
	return num*flg;
}
#define N 600005
#define LL long long
int n,A,B,C;
int V[N];
char s[N];int le;
int ch[N][26];LL sum[N];
int tot,rt,mxl;
int all,pos[N],len[N],val[N],st[N],ed[N];
void insert(int &i,int d,int k)
{
	if(!i)i=++tot;
	pos[all+d+1]=i;len[i]=d;val[all+d+1]=k;
	if(d>=le)return;
	insert(ch[i][s[d]-'a'],d+1,k);
}
int bel[N],D;
struct node{
	int l,r,id;
	bool operator < (const node &t)const{
		return bel[l]t.r);
	}
}q[N];
int g[N];
LL F(int x){return 1ll*x*(x-1)/2;}
LL gcd(LL x,LL y){return !y?x:gcd(y,x%y);}
int lp[N],rp[N],cnt[N];
bool check(int x){return (sum[x]&&1ll*B*sum[x]+1ll*A*len[x]>=1ll*C);}
LL ans,lans[N];
void add(int x)
{
	int p=pos[x],tmp=check(p);
	sum[p]+=val[x];
	if(!tmp&&check(p)&&(!cnt[g[len[p]]]++)){
		p=g[len[p]];
		lp[rp[p]]=p;
		rp[lp[p]]=p;
		ans+=F(rp[p]-p)+F(p-lp[p])-F(rp[p]-lp[p]);
	}
}
void del(int x)
{
	int p=pos[x],tmp=check(p);
	sum[p]-=val[x];
	if(tmp&&!check(p)&&(!(--cnt[g[len[p]]]))){
		p=g[len[p]];
		lp[rp[p]]=lp[p];
		rp[lp[p]]=rp[p];
		ans+=F(rp[p]-lp[p])-F(rp[p]-p)-F(p-lp[p]);
	}
}
int main()
{
	freopen("string.in","r",stdin);
	freopen("string.out","w",stdout);
	int Q,l,r,L,R,i,j;
	n=gi();A=gi();B=gi();C=gi();
	for(i=1;i<=n;i++)V[i]=gi();
	for(i=1;i<=n;i++){
		scanf("%s",s);le=strlen(s);
		mxl=max(mxl,le);
		insert(rt,0,V[i]);
		st[i]=all+1;all+=le+1;ed[i]=all;
	}
	for(i=1;i<=mxl;i++)g[i]=gi();
	Q=gi();
	D=int(sqrt(1.0*all+0.5));
	for(i=1;i<=all;i++)bel[i]=(i-1)/D+1;
	for(i=1;i<=Q;i++){q[i].l=st[gi()];q[i].r=ed[gi()];q[i].id=i;}
	sort(q+1,q+Q+1);
	
	int las=0;ans=0;
	for(i=1;i<=all;i++)sum[pos[i]]+=val[i];
	for(i=1;i<=tot;i++)if(check(i))cnt[g[len[i]]]++;
	for(i=1;i<=mxl;i++)
		if(cnt[i]){rp[lp[i]=las]=i;ans+=F(i-las);las=i;}
	rp[las]=mxl+1;ans+=F(mxl+1-las);
	
	//printf("initial:");for(int k=1;k<=mxl;k++)printf("%d ",cnt[k]);printf("\n");
		
	l=1;r=all;
	for(i=1,j=1;i<=bel[all]&&j<=Q;i++){
		L=(i-1)*D+1;R=min(all,i*D);
		for(;j<=Q&&bel[q[j].l]==i;j++){
			
			//printf("start:");for(int k=1;k<=mxl;k++)printf("%d ",cnt[k]);printf("\n");
				
			while(r>q[j].r)del(r--);
			while(lL)add(--l);
				
			//printf("end:");for(int k=1;k<=mxl;k++)printf("%d ",cnt[k]);printf("\n");
			//printf("\n");
		}
		while(r

 

 

 

 

 

 

题解

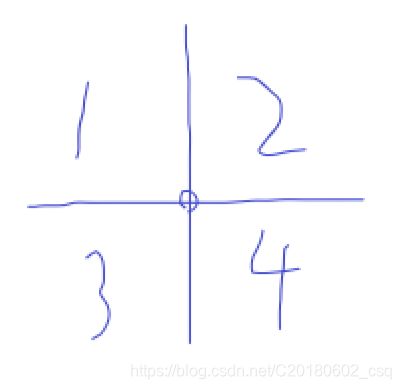
整体二分+网络流（这个问题本质上其实是保序回归L1问题）

考虑权值范围为[0,1]的情况

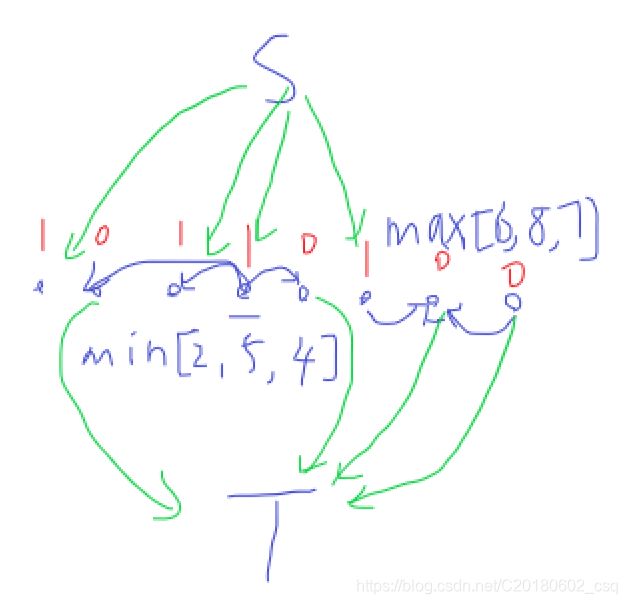
如图就是一种建图方法（蓝边边权为INF，绿边边权为1）

可以发现这样建图的话，如果一个被限制为最小值的点x的权值为1，且它管辖的区间范围种有权值为0的点

那么他就会贡献1的流量，也就是说，使它满足条件就会花费1的代价

这种建图方式本质其实就是最大权闭合图的建图方式

注意，这里要使用线段树优化建边，并且由于min、max限制的连边方式普通，还需要开两棵线段树分别进行优化

然后根据保序回归的那篇论文，把所有的点整体二分一下最终的权值，然后看是否满流就可以了？？？

表示看不懂论文

但是写代码还是会的。。。hhh

 

代码：（啊啊啊cnt一定要赋成1啊啊啊啊，调到凌晨1点，难受，第二天才发现错。。。）

#include
#include
#include
#include
using namespace std;
inline int gi()
{
	char c;int num=0,flg=1;
	while((c=getchar())<'0'||c>'9')if(c=='-')flg=-1;
	while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
	return num*flg;
}
#define N 50005
#define M 1000005
const int INF=0x3f3f3f3f;
int n,m,val[N],ans;
struct qnode{
	int l,r,t;
	qnode(){}
	qnode(int x,int y,int z){l=x;r=y;t=z;}
};
vector Q[N];
int fir[N],cur[N],nxt[M],to[M],cap[M],cnt;
void adde(int a,int b,int c)
{
	//printf("adde:%d %d %d\n",a,b,c);
	to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;cap[cnt]=c;
	to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;cap[cnt]=0;
}
#define lc i<<1
#define rc i<<1|1
struct node{
	int l,r,x;
}a[2][N];
int id[N],tot;
void build(int i,int l,int r)
{
	a[0][i].l=l;a[0][i].r=r;
	if(l==r){a[0][i].x=a[1][i].x=id[l];return;}
	int mid=(l+r)>>1;
	a[0][i].x=++tot;a[1][i].x=++tot;
	build(lc,l,mid),build(rc,mid+1,r);
	adde(a[0][i].x,a[0][lc].x,INF);
	adde(a[0][i].x,a[0][rc].x,INF);
	adde(a[1][lc].x,a[1][i].x,INF);
	adde(a[1][rc].x,a[1][i].x,INF);
}
void insert(int i,int l,int r,int p,int t)
{
	if(a[0][i].l>r||a[0][i].r &A)
{
	if(A.empty()) return;
	if(l==r){
		for(int i=0;i<(int)A.size();i++)
			ans+=(val[A[i]]>1,i,j;
	S=tot=1;T=++tot;
	for(i=0;i<(int)A.size();i++)
		id[i]=++tot;
	build(1,0,A.size()-1);
	for(i=0;i<(int)A.size();i++){
		for(j=0;j<(int)Q[A[i]].size();j++){
			qnode tmp=Q[A[i]][j];
			int x=lower_bound(A.begin(),A.end(),tmp.l)-A.begin();
			int y=upper_bound(A.begin(),A.end(),tmp.r)-A.begin()-1;
			if(x<=y) insert(1,x,y,id[i],tmp.t);
		}
	}
	for(i=0;i<(int)A.size();i++){
		if(val[A[i]]<=mid)adde(id[i],T,1);
		else adde(S,id[i],1);
	}
	while(bfs())
		memcpy(cur,fir,(tot+1)<<2),sap(S,INF);
	//bfs();
	vector L,R;
	for(i=0;i<(int)A.size();i++){
		if(dis[id[i]]!=-1)L.push_back(A[i]);
		else R.push_back(A[i]);
	}
	memset(fir,0,(tot+1)<<2);cnt=1;
	solve(l,mid,L),solve(mid+1,r,R);
}
vector ini;
int main()
{
	freopen("sequence.in","r",stdin);
	freopen("sequence.out","w",stdout);
	cnt=1;
	int i,x,mi=INF,mx=-INF,l,r,op;
	n=gi();m=gi();
	for(i=1;i<=n;i++){
		val[i]=gi();ini.push_back(i);
		mi=min(mi,val[i]);mx=max(mx,val[i]);
	}
	while(m--){
		op=gi();l=gi();r=gi();x=gi();
		Q[x].push_back(qnode(l,r,op));
	}
	solve(mi,mx,ini);
	printf("%d\n",ans);
}