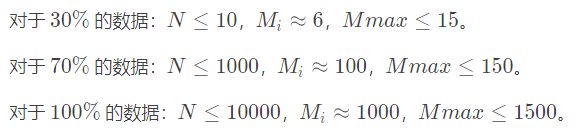字符串学习&总结（感觉主要是总结模板）

前言

1. 大二上寒假把字符串算法看完了，但是没有练题emm。差不多7个月过去了，忘得差不多了，再来总结一下。
2. 参考博客：oi-wiki
3. 先拉战线，把这些算法都过一遍，然后再慢慢刷题？？？
   1. 不然觉得无所谓，不珍惜时间（如果没有一个值得追求的目标，那确实不容易珍惜时间）
   2. 我觉得不只是字符串，其他算法也可以这样子做啦。
4. 上午刷题“kuangbin带你飞”专题计划——专题十六 KMP & 扩展KMP & Manacher刷累了，下午可以看看算法！！！提高学习效率是关键，要有目标：专攻字符串（看看能有多深入，学不懂了再深入学习其他算法）

（一）哈希：

搬走了：哈希yyds学习&总结（全）

导读

1. 两种哈希函数，不要弄混
   
2. M要选择尽量大的素数，B可以任意选择（一般来说，B也大点效果更好）
   
3. 错误率（hash改进：双哈希）
   
4. 子串哈希值（怎的突然变得简单了许多）
   
   1. $b^{r-l+1}$可以预处理然后$O(1)$查询
5. 哈希最重要的性质
   

HASH模板（哈希&双哈希）

//首先得说明，模板都是"xyz"=x*B^2+y*B+z
//结构体方便双哈希
//哈希值不同子串一定不同，哈希值相同子串不一定相同。双哈希最保险
//#define int long long感觉是必须的，因为B=23,M=1e9+7,,,
struct HASH {
    //不过好在HASH还是很快
    int B;     // B进制
    int M;     //大素数取余
    int b[N];  // b[i]=b^i%M
    int a[N];  //哈希前缀
    void init(int n, int x, int y) {
        b[0] = 1, B = x, M = y;
        for (int i = 1; i <= n; i++) b[i] = b[i - 1] * B % M;
    }
    //核心操作：求子串哈希值
    int get(int l, int r) {
        return (a[r] - a[l - 1] * b[r - l + 1] % M + M) % M;
    }
    //#################以上是基础操作 ，以下随题目:::
} h[2];

hash应用（hash牛逼克拉斯）:::::::::::::::

0. 核心操作：求子串哈希值

1. 字符串匹配

2. 允许k次失配的字符串匹配

3. 最长回文子串（hash操作简单，可解决的问题有点多啊！！！nice）

4. 最长公共子字符串（m个总长不超过n的非空字符串的最长公共子串）

1. m个字符串的最小长度可能远远达不到$n/m$，所以二分次数挺少的。。

5. 确定字符串中不同子字符串的数量

1. 复杂度$O(n)$???那没事了

hash实战

题目1：E. Compress Words（合并字符串&合并的时候前后缀去重）

1. E. Compress Words

2. 题意：
   
   

   1. n个字符串，总长度不超过$1e6$
   2. 从1到n合并所有串，合并两个串的时候，如果前面的串的后缀和后面的串的前缀相等，那么只留前面串的后缀或者后面串的前缀（去重）

3. 题解：hash，其他比如kmp算法应该也可以，但是hsah yyds!!!

4. 代码：

#include 
// #define int unsigned long long
#define int long long
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 1e6 + 10;

int n;
char c[N], s[N];
int cnt = 0;
//方便双哈希？
struct HASH {
    //#define int long long感觉是必须的，因为B=23,M=1e9+7,,,
    //不过好在HASH还是很快
    int B;     // B进制
    int M;     //大素数取余
    int b[N];  // b[i]=b^i%M
    int a[N];  //哈希前缀
    void init(int n, int x, int y) {
        b[0] = 1, B = x, M = y;
        for (int i = 1; i <= n; i++) b[i] = b[i - 1] * B % M;
    }
    int get(int l, int r) {
        return (a[r] - a[l - 1] * b[r - l + 1] % M + M) % M;
    }
    //#################以上是基础操作 ，以下随题目:::
} h[2];
int d[2][N];
void add() {
    int len = strlen(c + 1), mx = 0;
    for (int i = 1; i <= len; i++) {
        bool f = true;
        //双哈希--------循环（代码更容易写）
        for (int j = 0; j < 2; j++) {
            d[j][i] = (d[j][i - 1] * h[j].B + c[i]) % h[j].M;
            if (cnt < i)
                f = false;
            else if (h[j].get(cnt - i + 1, cnt) != d[j][i])
                f = false;
        }
        if (f) mx = i;
    }
    // dbg(mx);
    for (int i = mx + 1; i <= len; i++) {
        ++cnt;
        for (int j = 0; j < 2; j++) {
            h[j].a[cnt] = (h[j].a[cnt - 1] * h[j].B + c[i]) % h[j].M;
        }
        s[cnt] = c[i];
    }
}
signed main() {
    h[0].init(N - 1, 233, 1e9 + 7);
    h[1].init(N - 1, 2333, 1e9 + 9);
    cin >> n;
    while (n--) {
        cin >> c + 1;
        add();
    }
    cout << s + 1 << endl;
    return 0;
}

题目2：P3370 【模板】字符串哈希（求n个串中有多少个不同的串&怎么双哈希？？）

1. P3370 【模板】字符串哈希
2. 题目：
   
   
3. 提示：单哈希90分emmm
   1. 这个可怎么双哈希，我想每次都用双哈希
   2. 有了，求哈希值集合的大小的最大值（见代码）
4. 代码：

#include 
#define int long long
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 1500 + 10;

int n, m;
char c[N];
//方便双哈希？
struct HASH {
    //#define int long long感觉是必须的，因为B=23,M=1e9+7,,,
    //不过好在HASH还是很快
    int B;     // B进制
    int M;     //大素数取余
    int b[N];  // b[i]=b^i%M
    int a[N];  //哈希前缀
    void init(int n, int x, int y) {
        b[0] = 1, B = x, M = y;
        for (int i = 1; i <= n; i++) b[i] = b[i - 1] * B % M;
    }
    int get(int l, int r) {
        return (a[r] - a[l - 1] * b[r - l + 1] % M + M) % M;
    }
    //#################以上是基础操作 ，以下随题目:::
    int add() {
        m = strlen(c + 1);
        for (int i = 1; i <= m; i++) a[i] = (a[i - 1] * B + c[i]) % M;
        return a[m];
    }
} h[2];
signed main() {
    h[0].init(N - 1, 233, 1e9 + 7);
    h[1].init(N - 1, 2333, 1e9 + 9);
    cin >> n;
    set<int> st[2];
    while (n--) {
        // cin >> m;
        cin >> c + 1;
        for (int j = 0; j < 2; j++) {
            st[j].insert(h[j].add());
        }
    }
    int ans = 0;
    for (int j = 0; j < 2; j++) {
        int t = st[j].size();
        ans = max(ans, t);
    }
    cout << ans << endl;
    return 0;
}

（二）字符串匹配2：前缀函数与KMP算法（原来前缀函数才是关键，叫前缀函数算法得了）

引入

1. 前缀函数定义：注意是真前/后缀，即不能是字符串本身。
   
2. 理解前缀函数：
   

模板：计算前缀函数的最终算法

//在线算法：即，其实可以一个字符一个字符输入
struct KMP {
    //与其说是KMP算法，不如说是前缀函数算法。而KMP也只是它的一个应用
    int pi[N];  //前缀数组
    
    //得到前缀函数，即前缀数组的值
    //注意进入函数的是s还是s+1？
    //当然是s，我发现，我之前就，从来没写过s+1的kmp。（之后多刷题，再说吧）
    void get(char *s, int l) {
        for (int i = 1; i < l; i++) {
            int j = pi[i - 1];
            while (j > 0 && s[i] != s[j]) j = pi[j - 1];
            if (s[i] == s[j]) j++;
            pi[i] = j;
        }
    }

    //######################根据题目不同写不同的东西咯：


} kmp;

（前缀函数）应用

1. 在字符串中查找子串：Knuth-Morris-Pratt 算法（KMP）

1. 一般的题意：
   
2. 题解：（具体见题目1：模板题，还有代码）
   

题目1：P3375 【模板】KMP字符串匹配（查找字符串s在t中的位置，以及s的前缀函数）

1. 模板题：P3375 【模板】KMP字符串匹配
2. 题意：
   
   
3. 题解：s，t长度分别为n，m。
   1. 求出字符串s+’#’+t的前缀函数（下标从0开始！！！因为我不会从1开始emm），
   2. 然后遍历n+1~n+m，如果前缀函数为n则表示匹配，然后输出起始位置：i-(n-1)-n=i-2*n+1
   3. 这里还要求输出0~n-1的前缀函数
   4. 总之，抓住重点：求前缀函数，然后就是自己找规律了（当然很多规律也是要背的，要多做题熟悉的）。
4. 代码：

#include 
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 2e6 + 10;
char s[N], t[N];
int n, m;

//在线算法：即，其实可以一个字符一个字符输入
struct KMP {
    //与其说是KMP算法，不如说是前缀函数算法。而KMP也只是它的一个应用
    int pi[N];  //前缀数组

    //注意进入函数的是s还是s+1？
    //当然是s，我发现，我之前就，从来没写过s+1的kmp。（之后多刷题，再说吧）
    void get(char *s, int l) {
        for (int i = 1; i < l; i++) {
            int j = pi[i - 1];
            while (j > 0 && s[i] != s[j]) j = pi[j - 1];
            if (s[i] == s[j]) j++;
            pi[i] = j;
        }
    }

    //######################根据题目不同写不同的东西咯：
    void solve(int n, int len) {
        for (int i = n + 1; i < len; i++) {
            if (pi[i] == n) printf("%d\n", i - 2 * n + 1);
            //从1开始：为什么是i-2*n，这里还是要小推一下i-(n-1)-(n+1)，i-(n-1)是s+'#'+t中起点，再-(n+1)才是t中起点
            //从0开始：i-(n-1)-n=i-2*n+1
        }
        for (int i = 0; i < n; i++) printf("%d ", pi[i]);
    }
} kmp;
signed main() {
    cin >> t >> s;  //注意先输入哪一个串，在t中查找s
    n = strlen(s);
    m = strlen(t);
    //以下也算是kmp.init()部分吧。不过不是求pi函数的关键
    int len = n;
    s[len++] = '#';  //'#'为不可能出现的字符
    for (int i = 0; i < m; i++) s[len++] = t[i];
    // dbg(s + 1);
    kmp.get(s, len);  //注意是s还是s+1
    kmp.solve(n, len);
    return 0;
}

2. 字符串的周期（下标从0开始&最小周期T=n-pi[n-1]）

3. 统计每个前缀的出现次数

4. 一个字符串中本质不同子串的数目

5. 字符串压缩

6. 根据前缀函数构建一个自动机

（三）拓展KMP（Z函数/E-KMP）

引入

1. 约定：字符串下标以0为起点。
2. KMP最重要的东西就是前缀函数，E-KMP最重要的函数就是Z函数：
   
3. 复杂度：$O(n)$求Z函数，求前缀函数的复杂度也是$O(n)$。
   
4. 理解Z函数：见 z 函数的定义
   

线性算法求 Z 函数原理

总结核心就是：维护右端点最靠右的匹配段

模板：求 Z 函数

struct EKMP {
    //首先约定：字符串下标从0开始
    //可能是有必要，在求z之前，对z进行初始化为0 的，特别是z[0]=n的时候。
    int z[N];  // z[i]定义：s和s[i,n-1]的最长公共前缀的长度。
    //叫做z函数，特别的z[0]=0（也不一定，有时候题目就会暗示z[0]=n，注意变通就ok了）
    void z_function(char *s, int n) {
        int l = 0, r = 0;  //算法的过程中我们维护右端点最靠右的匹配段[l,r]
        for (int i = 1; i < n; i++) {
            //如果i<=r，[i,r]和[i-l,r-l]与s的最长公共前缀应该相等
            if (i <= r && z[i - l] < r - i + 1) {
                z[i] = z[i - l];
            } else {
                z[i] = max(0, r - i + 1);
                while (i + z[i] < n && s[z[i]] == s[i + z[i]]) ++z[i];
            }
            if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
            //注意每次需要O(1)更新一下下
        }
        // z[0]=n;//有时候题目会有这个要求，但是有时候就z[0]=0
    }

    //这里也是，根据题目要求不同有不同操作：：：

} ekmp;

应用

1. 匹配所有子串：相比KMP方便一点点点点，不用i-2*n+1 emm

1. 和KMP一毛一样，不过这里不用i-2*n+1。

2. 本质不同子串数：比HASH还是快了不少（$O(n^{2}logn)=>O(n^2)$）

总结一下算法思想（挺简单的）：

1. 已知当前前缀串 s 的本质不同子串的数目，再加一个字符 c ，会增加多少个 s 中没有出现的子串呢？
2. 另t=c+s（注意是反串），然后可以增加|t|-Zmax个新子串。即$O(n)$可以求解：增加一个字符，增加了多少子串。
3. 所以答案是$O(n^2)$的。（比哈希快挺多）

3. 字符串整周期：也挺方便的（注意这里是整周期，KMP的话还需要小处理一下）

总结：

1. 周期就是最小的，满足i+z[i]=n的i。

刷题

（四）manacher算法

（五）字典树（Trie）

字典树模板

struct Trie {
    // N大于可能出现的字符的总数
    int ch[N][30], cnt;
    int tag[N];  //给结尾打标记，表示这个字符串的数量
    //插入字符串，注意这里下标从0开始
    void insert(char *s, int l) {
        int p = 0;
        for (int i = 0; i < l; i++) {
            int c = s[i] - 'a';
            if (!ch[p][c]) ch[p][c] = ++cnt;  //如果没有，就添加结点
            p = ch[p][c];
        }
        tag[p]++;  //一般赋值为1就ok了
    }
    //查找字符串
    int query(char *s, int l) {
        int p = 0;
        for (int i = 0; i < l; i++) {
            int c = s[i] - 'a';
            if (!ch[p][c]) return 0;
            p = ch[p][c];
        }
        return tag[p];  //返回个数，一般来说为1
    }
    //##################其他操作（依题而变）：：：：：：：：：：：

} trie;

引入

1. 先放一张图：
   
2. 这棵字典树用边来代替字母：
   

应用

1. 检索字符串（查找字符串是否在“字典”中出现过）

题目1：P2580 于是他错误的点名开始了（字典树最基本的操作：插入&查询）

1. P2580 于是他错误的点名开始了
2. 题意：
   
   
3. 题解：
   
4. 代码：

#include 
// #define int long long
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 1e4 * 50 + 10;  // 5e4
int n, m;
char s[60];
struct Trie {
    // N大于可能出现的字符的总数
    int ch[N][30], cnt;
    int tag[N];  //给结尾打标记，表示这个字符串的数量
    //插入字符串，注意这里下标从0开始
    void insert(char *s, int l) {
        int p = 0;
        for (int i = 0; i < l; i++) {
            int c = s[i] - 'a';
            if (!ch[p][c]) ch[p][c] = ++cnt;  //如果没有，就添加结点
            p = ch[p][c];
        }
        tag[p]++;  //一般赋值为1就ok了
    }
    //查找字符串
    int query(char *s, int l) {
        int p = 0;
        for (int i = 0; i < l; i++) {
            int c = s[i] - 'a';
            if (!ch[p][c]) return 0;
            p = ch[p][c];
        }
        return tag[p];  //返回个数，一般来说为1
    }
    //##################其他操作（依题而变）：：：：：：：：：：：
    int ask(char *s, int l) {
        int p = 0;
        for (int i = 0; i < l; i++) {
            int c = s[i] - 'a';
            if (!ch[p][c]) return -1;  //表示不存在
            p = ch[p][c];
        }
        return p;  //返回尾结点，然后我们标记
    }
} trie;
signed main() {
    cin >> n;
    while (n--) {
        cin >> s;
        trie.insert(s, strlen(s));
    }
    int mp[N];
    cin >> m;
    while (m--) {
        cin >> s;
        int t = trie.ask(s, strlen(s));
        if (t == -1)
            puts("WRONG");
        else {
            if (!mp[t])
                mp[t] = 1, puts("OK");
            else
                puts("REPEAT");
        }
    }
    return 0;
}

2. AC自动机

3. 维护异或极值

4. 维护异或和

插入&删除

全局加1

5. 01Trie合并

6. 可持久化字典树

（六）AC自动机