堆排序算法---C语言实现（超详细解析！！！！）

目录

一、前言

二、堆排序 

 方法一（自己写一个堆，在进行排序）

时间复杂度分析 

方法二（直接在数组上建堆） 

向上调整建堆 

 向下调整建堆 

时间复杂度分析（向上建堆和向下建堆熟优？）

 升序（排序）建大堆还是小堆？

 完整的堆排序（升序）图形和代码演示

三、共勉

---

一、前言

在上一篇博客，已经详细的讲解了 堆的创建、插入数据、删除数据、销毁，等操作。其实在我们平时的应用中，堆用到的最多的还是-------------堆排序和Topk问题。所以本篇博客，就来详细的讲解以上问题。

如果对----- 堆和二叉树还不太了解的可以取这里看看 O！！

详解二叉树和堆

二、堆排序 

• 假如我们有一串乱序数组，如下：
• 

       现在想要对它进行排序，按照我们之前学过的知识，想要单纯的实现排序其实并不难，可以直接暴力排序，也可以冒泡排序，甚至使用库函数qsort进行排序……

       但是，既然近期学习了堆，那么堆的一个重要应用就是进行堆排序，这里先简要提下：堆排序即快排的一种。在后面的学习中，我将为大家继续展开其它更多样的快排。今儿个就向各位浅谈下快排之一：堆排序

 方法一（自己写一个堆，在进行排序）

✨思路：在上篇博文中，我们模拟实现了堆，实现后即可对一串乱序数组进行堆排序。假设我们排升序，且堆为小根堆。实现过程非常简单。

1.首先，把数组的每个元素（HeapPush）插入到堆中。
2.其次，我们深知小根堆的堆顶是最小的数字，依次遍历堆顶（HeapTop）的元素，将堆顶元素赋值到数组里，从下标0开始，赋值后删除（HeapPop）堆顶元素，++数组下标。此时堆就会重新调整，最终堆顶依旧是最小的，再重复上述赋值堆顶到数组的操作，直到堆为空（HeapEmpty）
⭐：代码如下：

void HPSort(int* a, int n)
{
    HP ps;  // 定义一个顺序表结构体
    // 对堆结构进行初始化
    HPInit(&ps);
    // 向堆结构中进行尾插数据
    for (int i = 0; i < n; i++)
    {
        HPPush(&ps, a[i]);
    }

    int i = 0;
    // 当堆结构不为空时
    while (!HPEmpty(&ps))
    {
        a[i++] = HPTop(&ps);
        HPPop(&ps);
    }
    printf("进行堆排序：\n");
    for (int j = 0; j < n; j++)
    {
        printf("%d ", a[j]);
    }
}

int main()
{
    // 堆排序测试
    int a[100];
    int j = 0;
    int sum ;
    printf("请输入你要插入堆的数据(-1结束)：>\n");
    for (int i = 0; i < 100; i++)
    {
        scanf("%d", &sum);
        if (sum == -1)
        {
            break;
        }
        a[j++] = sum;
    }

    HPSort(a, j);
    return 0;
}

⭐：实验效果图

时间复杂度分析 

段一：

for (int i = 0; i < n; i++)
    {
        HPPush(&ps, a[i]);
    }

此段代码的时间复杂度为O(N*logN)，因为HeapPush函数的内部执行过程就是把数组的每个元素插入堆中，有N次。接着，每插入一个数据都要重新向上调整（AdjustUp）高度次以确保为堆，每个都要调整高度次，高度为logN，综上此段为O(N*logN)

段二：

while (!HPEmpty(&ps))
    {
        a[i++] = HPTop(&ps);
        HPPop(&ps);
    }

此段的时间复杂度同样为O(N*logN)，原理跟上一段类似，不过多赘述。

✨分析：综上，时间复杂度为O(N*logN)，确实比我们先前的冒泡排序O(N^2)要快不少。但是，这个方法排序是及其不好的，因为难道说为了实现堆排序还要自己手写一个完整的堆吗？这么复杂的实现堆的过程还不如不用堆排序了，这种伤敌一千，自损八百的感脚实在是难受。更何况此法的空间复杂度也是很大的，达到了惊人的O(N)。原因是实现堆的过程是动态开辟的，所以空间复杂度自然是O(N)。可不可以换一更优的方法，但同样是利用堆的思想实现快排呢？

✨我们目前的要求：

1. 依旧是堆的思想
2. 时间复杂度O(N*logN)
3. 空间复杂度O(1)

方法二（直接在数组上建堆） 

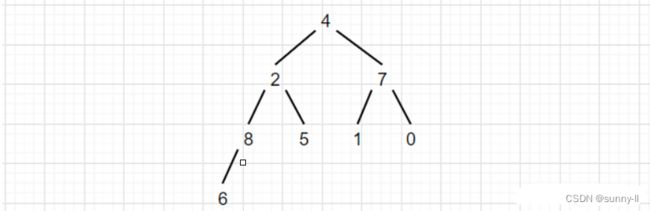
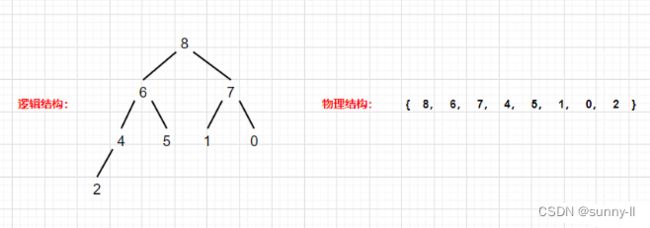
先看一下这个乱序数组

既然上文说到可以直接把它看作二叉树，那不妨把逻辑结构画出来看看：

接下来，我们就要进行建堆了，有两种方法：

1. 使用向上建堆，插入数据的思想建堆
2. 使用向下调整建堆

向上调整建堆 

✨思路：首先，我们把第一个数字看成堆，也就是4，当第二个数字插入进去的时候，进行向上调整算法，使其确保为小堆，向上调整的算法在上篇博文已详细讲解过，不过多赘述。具体插入数据过程就是遍历数组，确保数组里每一个数进行向上调整算法

✨：向上/下调整算法： 详解向上/下调整算法
 

✨：画图演示：（小根堆）

✨：代码演示

void swap(HPDatatype* x, HPDatatype* y)
{
	int temp = 0;
	temp = *x;
	*x = *y;
	*y = temp;
}

void AdjustUp(HPDatatype* a, int child)
{
	// 计算父亲的小标
	int parent = (child - 1) / 2;
	// 当 child 的小标大于 0 就继续 （也就小于是根节点位置）
	while (child > 0)
	{
		// 小堆 <
		// 大堆 >
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

// 向上调整建堆
void Heap(int* a, int n)
{
    //建堆
    int i = 0;
    for (i = 1; i < n; i++) //应该从i=1时遍历，因为第一个数据在堆里不需要调整，后续再插入时调整
    {
        AdjustUp(a, i);
    }
    printf("堆：\n");
        for (int j = 0; j < n; j++)
        {
            printf("%d ", a[j]);
        }
}



int main()
{
    // 建堆测试
    int a[100];
    int j = 0;
    int sum ;
    printf("请输入你要插入堆的数据(-1结束)：>\n");
    for (int i = 0; i < 100; i++)
    {
        scanf("%d", &sum);
        if (sum == -1)
        {
            break;
        }
        a[j++] = sum;
    }

    Heap(a, j);
    return 0;
}

✨：效果演示：

符合小根堆的性质

 向下调整建堆 

• 问题：能直接进行向下建堆吗？

答案：不能

解析：首先回顾下使用向下调整的前提是什么？必须得确保根结点的左右子树均为小堆才可，而这里，数组为乱序的，无法直接使用。

• 解决办法：从倒数第一个非叶结点开始向下调整，从下往上调

✨：分析：从该解决方案中，我们首先要找到这个倒数第一个非叶结点的数在哪？其实最后一个结点的父亲即为倒数第一个非叶结点。当我们找到这个非叶结点时，把它和它的孩子看成一个整体，进行向下调整。调整后，再将次父节点向前挪动，再次向下调整，依次循环下去。

• 再回顾下父亲和孩子间的关系：

1. leftchild = parent*2 + 1
2. rightchild = parent*2 + 2
3. parent = (child - 1) / 2

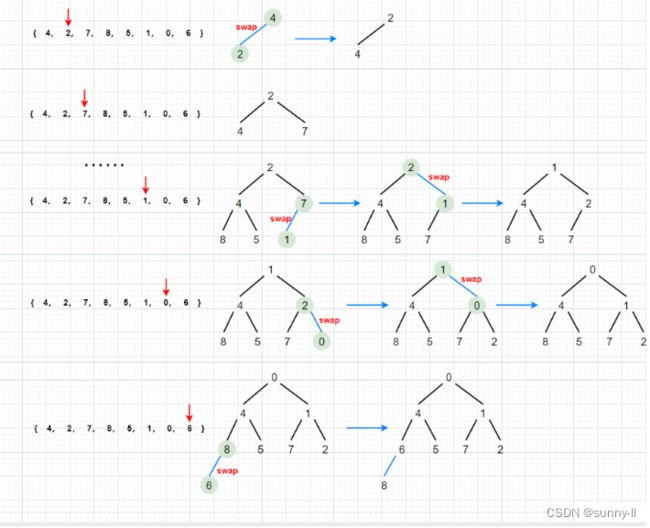
✨：画图分析

✨：代码演示：建小堆（数据：4 ，2，7，8，5，0，6）

void swap(HPDatatype* x, HPDatatype* y)
{
	int temp = 0;
	temp = *x;
	*x = *y;
	*y = temp;
}

// 向下调整
// 向下调整的前提：后面的数据是堆
void AdjustDown(HPDatatype* a, int n, int parent)
{
	// 左孩子
	int child = parent * 2 + 1;
	// 孩子可能会超出数组范围
	while (child < n)
	{
		// 如果右孩子小于左孩子
		// 找出小的那个孩子
		// 保证右孩子存在且不越界
		// 大堆 >
		// 小堆 <
		if (child + 1 < n && a[child+1] < a[child])
		{
			//跳转到有孩子那里
			child++;
		}
		// 开始向下调整
		// 大堆 >
		// 小堆 <
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}

	}
}

// 向下调整建堆
void Heap(int* a, int n)
{
    //建堆
    int i = 0;
    for (int i = ((n - 1) - 1) / 2; i >= 0; i--)
      {
           // 给定一个 a 数组，从 i 这个位置进行建堆， n 表示数组的大小
           AdjustDown(a, n, i);
      }
    printf("堆：\n");
        for (int j = 0; j < n; j++)
        {
            printf("%d ", a[j]);
        }
}



int main()
{
    // 建堆测试
    int a[100];
    int j = 0;
    int sum ;
    printf("请输入你要插入堆的数据(-1结束)：>\n");
    for (int i = 0; i < 100; i++)
    {
        scanf("%d", &sum);
        if (sum == -1)
        {
            break;
        }
        a[j++] = sum;
    }

    Heap(a, j);
    return 0;
}

✨：效果演示：

符合小根堆的性质

时间复杂度分析（向上建堆和向下建堆熟优？）

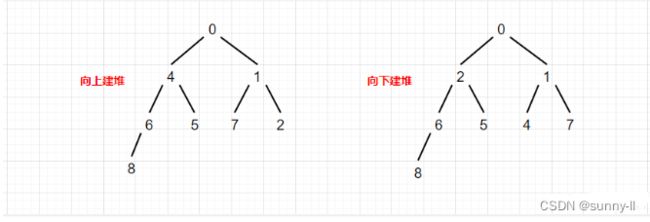
首先，我们画张图看下向上和向下建堆后的样子。

从上图中，我们可以看出，使用不同的方式建堆最后的样子是不同的，那哪种方式好呢？

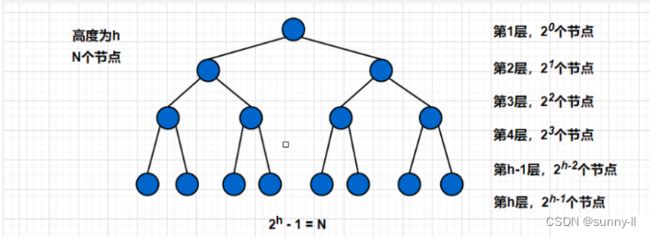
✨:接下来，我将通过时间复杂度的方式为大家解惑：以一颗满二叉树为例：

✨向上建堆的时间复杂度：

时间复杂度计算的是其调整的次数，根据上文的知识我们已经知晓其是从数组的第二个元素开始的，也就是可以理解为第二层的第一个节点。计算的思想非常简单：计算每层有多少个节点乘以该层的高度次，然后累计相加即可。如下：

通过计算得知：向上建堆的时间复杂度为O(N*logN)

✨向下建堆的时间复杂度：

向下调整我们前面已经知道它是从倒数第1个非叶节点开始调整的，每层的调整次数为，该层的节点个数*该层高度减1，一直从第1层开始调直至倒数第2层，并将其依次累加，此计算过程和向上调整差不多，都是等比*等差的求和，过程如下：

 通过计算得知：向下建堆的时间复杂度为O(N)

通过上述计算，我们得到如下：

1. 向上建堆：O(N*logN)
2. 向下建堆：O(N)

由此可见，使用向下建堆的方式更优，其时间复杂度较小。当然，使用向上建堆也是可以的，只不过向下建堆更好一点。

 升序（排序）建大堆还是小堆？

✨思考：排升序，建小堆可以吗？-- 可以是可以，但没啥意思。
首先对 n 个数建小堆，选出最小的数，接着对剩下的 n-1 个数建小堆，选出第2小的数，不断重复上述过程……。建 n 个数的堆时间复杂度是O(N)，所以上述操作时间复杂度为O(N2)，效率太低，尤其是当数据量大的时候，效率更低，同时堆的价值没有被体现出来，还不如用直接排序。

【最佳方法】排升序，因为数字越来越大，需要找到最大的数字，得建大堆

1. 首先对 n 个数建大堆。
2. 将最大的数（堆顶）和最后一个数交换，把最大的数放到最后。
3. 前面 n-1 个数的堆结构没有被破坏（最后一个数不看做堆里面的），根节点的左右子树依旧是大堆，所以我们进行一次向下调整成大堆即可选出第2大的数，放到倒数第二个位置，然后重复上述步骤……。

【时间复杂度】：建堆时间复杂度为O(N)，向下调整时间复杂度为O(logN)，这里我们最多进行N-2次向下调整。

所以堆排序时间复杂度为 ：O = O(N) + O(N-2)*O(logN) = O(N*logN)，效率是很高的。

✨解决方案：升序建大堆，降序建小堆

 完整的堆排序（升序）图形和代码演示

• 先看下建好大堆的样子：
• 
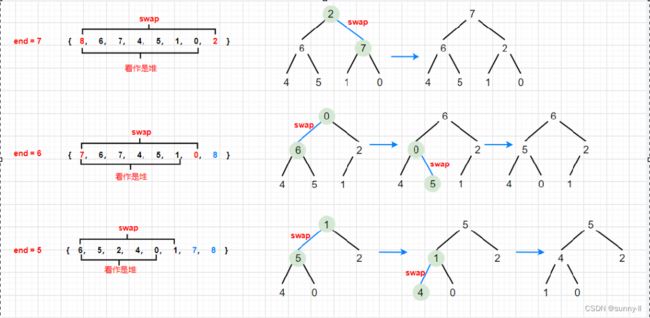
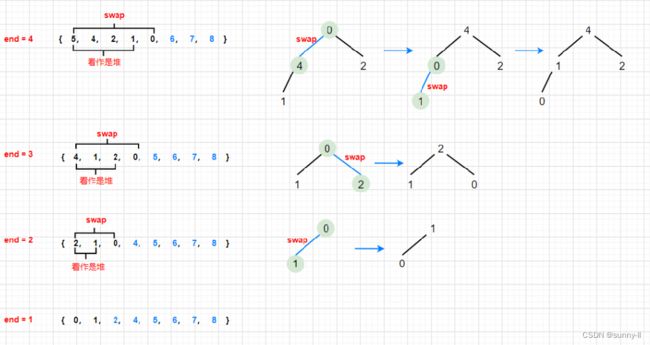
• ✨思路：首先，得明确我们建堆后，此时堆顶就是最大的数据，现在我们把第一个数字和最后一个数字交换，把最后一个数字不看做堆里的，只需要数组个数N--即可。此时的左子树和右子树依旧是大堆，再进行向下调整即可。
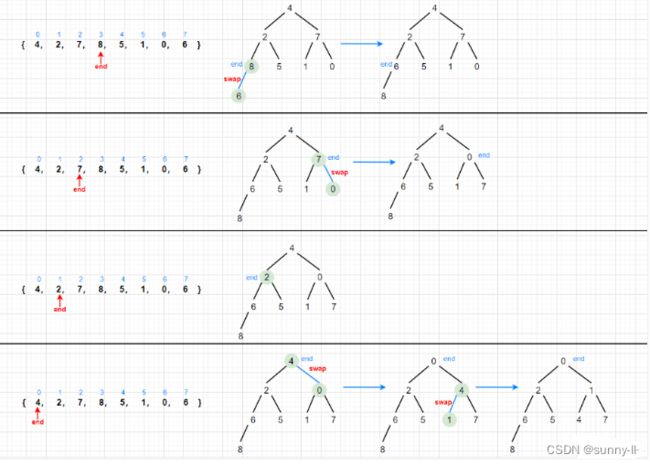
• 画图解析过程：
• 
• 
• ✨：代码演示：

• #include 
  #include 
  #include 
  #include 
  
  
  // 数据类型存储
  typedef int HPDatatype;
  
  // 数据交换
  void Swap(HPDatatype* x, HPDatatype* y)
  {
  	HPDatatype temp = 0;
  	temp = *x;
  	*x = *y;
  	*y = temp;
  }
  
  // HPDatatype* a ：表述动态数组
  // n :表示堆内（数组内）的数据个数
  // parent :父节点的下标（开始在根节点）
  void AdjustDown(HPDatatype* a, int n, int parent)
  {
  	// 左孩子
  	int child = parent * 2 + 1;
  	// 防止孩子跑出数组范围(最后一个节点为叶子节点)
  	while (child < n)
  	{
  		// 判断左右孩子那个大，将大的与父节点进行交换
  		// child+1 < n 表示确保右孩子存在
  		//  小堆 if (child + 1 < n && a[child] > a[child+1])
  		if (child + 1 < n && a[child] < a[child+1])
  		{
  			// 如果右孩子比左孩子大
  			child++;
  		}
  
  		// 开始向下调整
  		// 小堆：if (a[child] < a[parent])
  		if (a[child] > a[parent])   // 大堆
  		{
  			Swap(&a[child], &a[parent]);
  			parent = child;
  			child = parent * 2 + 1;
  		}
  		else
  		{
  			break;
  		}
  	}
  }
  
  
  void HPSort(int* a, int n)
  {
  	// 在原有的数据上（数组）创建一个堆
  	// 从倒数第一个非叶子节点的子树开始调整(最后一个节点的父亲)
  	for (int i = ((n - 1) - 1) / 2; i >= 0; i--)
  	{
  		AdjustDown(a, n, i);
  	}
  
  	// 升序建大堆（根位置和最后的位置交换）
  
  	int end = n - 1; //最后一个叶子节点下标
  	while (end > 0)
  	{
  		Swap(&a[0], &a[end]);
  		// 开始向下调整
  		AdjustDown(a, end, 0);
  		end--;
  	}
  	printf("堆排序结果展示：\n");
  	for (int j = 0; j < n; j++)
  	{
  		printf("%d ", a[j]);
  	}
  }
  
  int main()
  {
  	// 堆排序测试
  	int a[100];
  	int j = 0;
  	int sum;
  	printf("请输入你要插入堆的数据(-1结束)：>\n");
  	for (int i = 0; i < 100; i++)
  	{
  		scanf("%d", &sum);
  		if (sum == -1)
  		{
  			break;
  		}
  		a[j++] = sum;
  	}
  
  	HPSort(a, j);
  	return 0;
  }

  ✨：效果演示：

• 

三、共勉

以下就是我对数据结构---堆排序的理解，如果有不懂和发现问题的小伙伴，请在评论区说出来哦，同时我还会继续更新对数据结构-------堆的应用TopK问题，请持续关注我哦！！！！