数据结构与算法(十三)——红黑树1
Python微信订餐小程序课程视频
https://edu.csdn.net/course/detail/36074
Python实战量化交易理财系统
https://edu.csdn.net/course/detail/35475目 录
- 一、概述
- 1、介绍
- 2、左旋(重要)
- 3、右旋(重要)
- 二、插入
- 1、左左
- 2、左右
- 3、右右(与左左对称)
- 4、右左
- 5、总结
- 三、删除
返回顶部## 一、概述
1、介绍
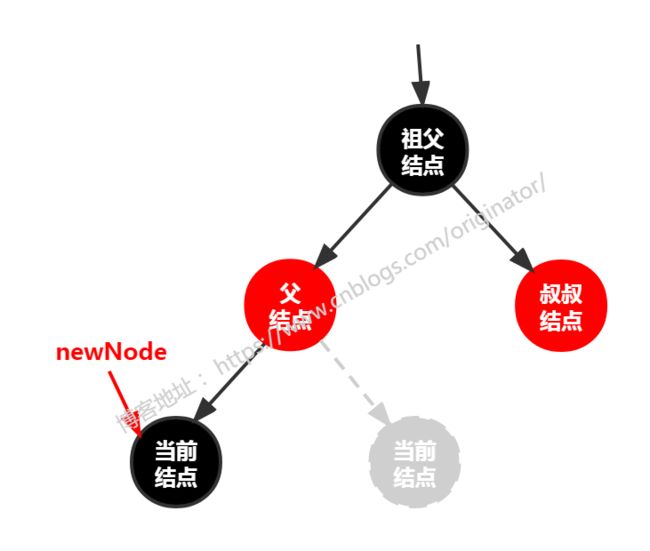
红黑树是一种自平衡的排序二叉树,常用于关联数组、字典,在各种语言的底层实现中被广泛应用,Java 的 TreeMap 和 TreeSet 就是基于红黑树实现的,在 JDK 8 的HashMap中也有应用。 红黑树是在排序二叉树的基础上定义的,且还要满足以下性质(重要):(请务必先学习排序二叉树,排序二叉树先看这篇 二叉树) (1)每个结点要么是黑色,要么是红色。 (2)根结点是黑色。 (3)所有叶子结点都是黑色(这里说的叶子结点指 NIL 结点,空结点,即:空结点为黑色)。 (4)从任意一个结点到其所有叶子结点,所经过的黑色结点数目必须相等。 (5)所有红色结点的两个孩子结点必须是黑色(即,红色结点不能连续)。 代码示例:红黑树-树结点结构
1 protected static class RBNodeextends Comparable> {
2 private T value;
3 // 默认为 红色 结点
4 private boolean red = true;
5
6 private RBNode left;
7 private RBNode right;
8 private RBNode parent;
9 }
树结点关系
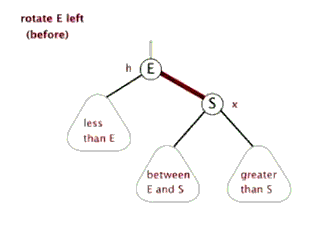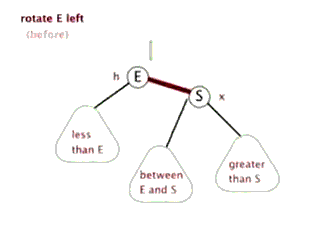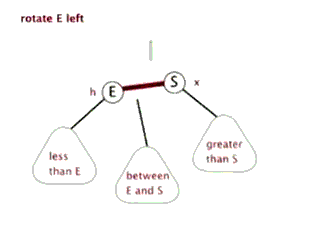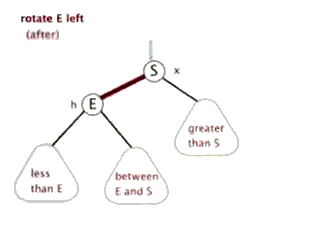
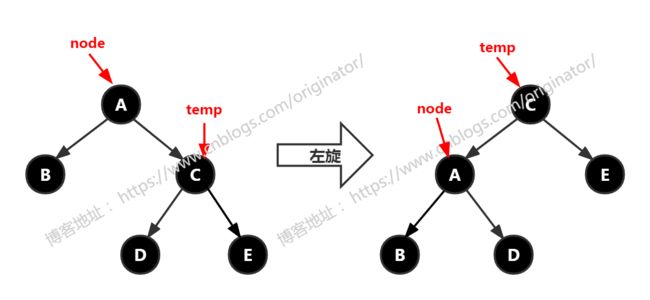
2、左旋(重要)
动图:
代码示例:对 node 左旋
1 // 左旋
2 private void leftRotate(RBNode node) {
3 if (node == null) {
4 return;
5 }
6 final RBNode p = node.parent;
7
8 // 左旋. 应该认为 temp 不为null
9 final RBNode temp = node.right;
10 node.right = temp.left;
11 if (temp.left != null) {
12 // 该结点可能不存在
13 temp.left.parent = node;
14 }
15
16 temp.left = node;
17 node.parent = temp;
18
19 // 旋转完成.修正根结点与父结点
20 // 1.node为根结点
21 if (node == root) {
22 root = temp;
23 temp.parent = null;
24 return;
25 }
26
27 // 2.node不为根结点
28 // node 为父结点的右孩子
29 if (node == p.right) {
30 p.right = temp;
31 } else {
32 p.left = temp;
33 }
34 temp.parent = p;
35 }
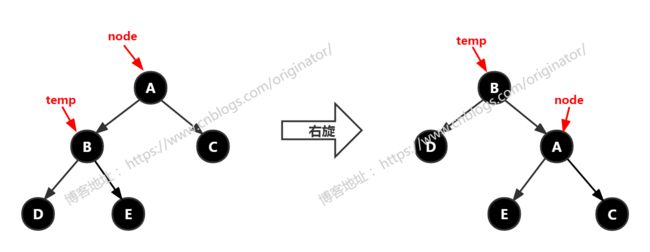
3、右旋(重要)
动图:
代码示例:对 node 右旋
1 // 右旋
2 private void rightRotate(RBNode node) {
3 if (node == null) {
4 return;
5 }
6
7 final RBNode p = node.parent;
8
9 // 右旋. 应该认为 temp 不为null
10 final RBNode temp = node.left;
11 node.left = temp.right;
12 if (temp.right != null) {
13 // 该结点可能不存在
14 temp.right.parent = node;
15 }
16
17 temp.right = node;
18 node.parent = temp;
19
20 // 旋转完成.修正根结点与父结点
21 // 1.node为根结点
22 if (node == root) {
23 root = temp;
24 temp.parent = null;
25 return;
26 }
27
28 // 2.node不为根结点
29 // node 为父结点的右孩子
30 if (node == p.right) {
31 p.right = temp;
32 } else {
33 p.left = temp;
34 }
35 temp.parent = p;
36 }
返回顶部## 二、插入
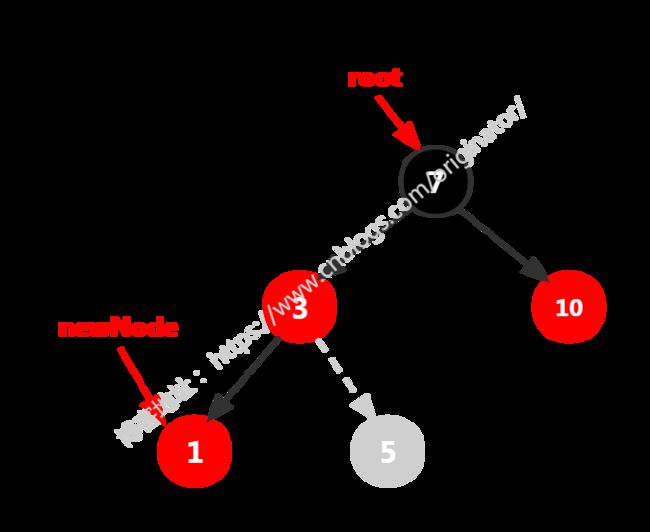
由于树的左子树和右子树是对称的,所以只讨论一边的情况即可。插入的原则满足排序二叉树的规则。而红黑树的插入还要满足红黑树的性质,所以插入完成后,还要对红黑树进行调整。调整的原则(重要): (1)按排序二叉树的插入规则插入新结点(newNode)。 (2)新插入的结点默认为红色。 (3)若 newNode 为根结点,则变为黑色,插入完毕。 (4)若 newNode 不为根结点,若其父结点为黑色,插入完毕。 (5)若 newNode 不为根结点,若其父结点为红色,则按下面的情况讨论(下面也主要讨论这种情况)。 以 {7, 3, 10, 1(5)} 为例,添加 {7, 3, 10} 的结果很容易理解。
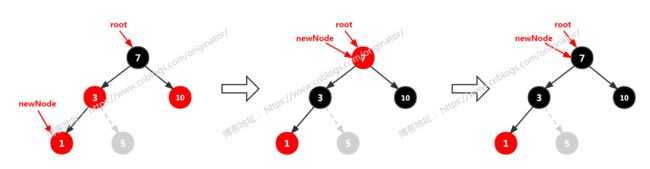
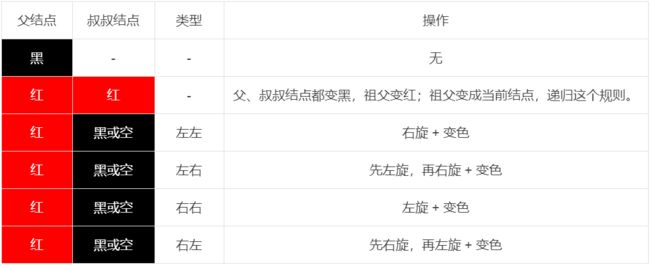
插入1(5)时, 情况一:newNode(1或5) 的叔叔结点(10)存在且为红色。 调整方案:父结点(3)与叔叔结点(10)变为黑色;祖父结点变为红色;新增结点 newNode 指向祖父结点(7),做递归的调整(这里newNode == root,则变为黑色即可)。
情况二:newNode(1或5) 的叔叔结点(10)不存在,或者为黑色。 调整方案:分为左左、左右、右右、右左讨论。(下面的讨论中,不妨将叔叔结点画为黑色)
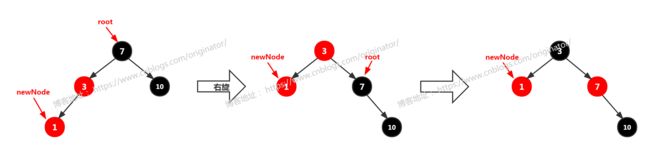
1、左左
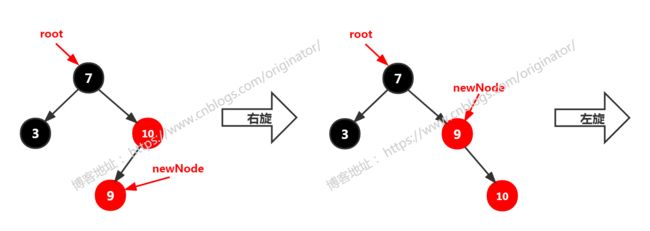
左左:newNode == 祖父结点的左孩子的左孩子。 调整方案:先对祖父结点(7)右旋;父结点变为黑色,祖父结点变为红色。
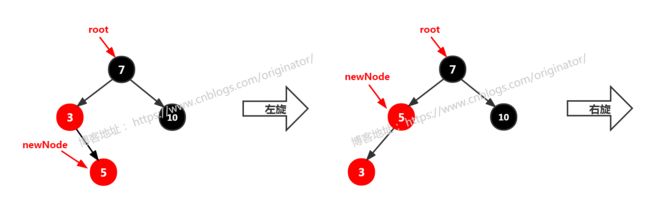
2、左右
左右:newNode == 祖父结点的左孩子的右孩子。 调整方案:先对父结点(3)左旋;后续调整同"左左"的方案。(需注意newNode的位置不同)
3、右右(与左左对称)
右右:newNode == 祖父结点的右孩子的右孩子。 调整方案:先对祖父结点(7)左旋;父结点变为黑色,祖父结点变为红色。
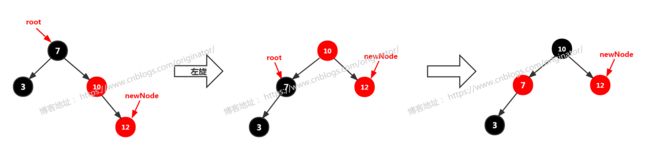
4、右左
右左:newNode == 祖父结点的右孩子的左孩子。 调整方案:先对父结点(10)右旋;后续调整同"右右"的方案。(需注意newNode的位置不同)
5、总结
代码示例:完整的红黑树插入及调整
![]()
![]()
1 public class RBTreeextends Comparable> {
2 // 根结点
3 private RBNode root;
4
5 public RBTree() {
6 }
7
8 public RBTree(T[] arr) {
9 if (arr == null || arr.length == 0) {
10 return;
11 }
12
13 for (T i : arr) {
14 this.add(i);
15 }
16 }
17
18 // 添加结点
19 public void add(T value) {
20 RBNode newNode = new RBNode<>(value);
21 if (root == null) {
22 root = newNode;
23 newNode.red = false;
24 return;
25 }
26
27 // 1.添加
28 this.add(root, newNode);
29
30 // 2.调整
31 this.fixUp(newNode);
32 }
33
34 private void fixUp(RBNode newNode) {
35 if (newNode == root) {
36 newNode.red = false;
37 return;
38 }
39
40 // newNode 的父结点为黑色
41 if (!newNode.parent.red) {
42 return;
43 }
44
45 /* 1.newNode 的叔叔结点存在且为红色。*/
46 final RBNode uncle = newNode.getUncle();
47 if (uncle != null && uncle.red) {
48 newNode.parent.red = false;
49 uncle.red = false;
50
51 newNode.parent.parent.red = true;
52 this.fixUp(newNode.parent.parent);
53 } else {
54 /* 2.newNode 的叔叔结点不存在,或者为黑色。*/
55 final RBNode grandFather = newNode.getGrandFather();
56 // 2.1左左
57 if (newNode == grandFather.left.left) {
58 this.rightRotate(grandFather);
59 newNode.parent.red = false;
60 grandFather.red = true;
61 }
62 // 2.2左右
63 else if (newNode == grandFather.left.right) {
64 this.leftRotate(newNode.parent);
65 this.rightRotate(grandFather);
66 newNode.red = false;
67 grandFather.red = true;
68 }
69 // 2.3右右
70 else if (newNode == grandFather.right.right) {
71 this.leftRotate(grandFather);
72 newNode.parent.red = false;
73 grandFather.red = true;
74 }
75 // 2.4右左
76 else if (newNode == grandFather.right.left) {
77 this.rightRotate(newNode.parent);
78 this.leftRotate(grandFather);
79 newNode.red = false;
80 grandFather.red = true;
81 }
82 }
83 }
84
85 // 按 排序二叉树 的规则插入结点
86 private void add(RBNode root, RBNode newNode) {
87 if (newNode.value.compareTo(root.value) <= 0) {
88 if (root.left == null) {
89 root.left = newNode;
90 newNode.parent = root;
91 } else {
92 this.add(root.left, newNode);
93 }
94 } else {
95 if (root.right == null) {
96 root.right = newNode;
97 newNode.parent = root;
98 } else {
99 this.add(root.right, newNode);
100 }
101 }
102 }
103
104 // 左旋
105 private void leftRotate(RBNode node) {
106 if (node == null) {
107 return;
108 }
109 final RBNode p = node.parent;
110
111 // 左旋. 应该认为 temp 不为null
112 final RBNode temp = node.right;
113 node.right = temp.left;
114 if (temp.left != null) {
115 // 该结点可能不存在
116 temp.left.parent = node;
117 }
118
119 temp.left = node;
120 node.parent = temp;
121
122 // 旋转完成.修正根结点与父结点
123 // 1.node为根结点
124 if (node == root) {
125 root = temp;
126 temp.parent = null;
127 return;
128 }
129
130 // 2.node不为根结点
131 // node 为父结点的右孩子
132 if (node == p.right) {
133 p.right = temp;
134 } else {
135 p.left = temp;
136 }
137 temp.parent = p;
138 }
139
140 // 右旋
141 private void rightRotate(RBNode node) {
142 if (node == null) {
143 return;
144 }
145
146 final RBNode p = node.parent;
147
148 // 右旋. 应该认为 temp 不为null
149 final RBNode temp = node.left;
150 node.left = temp.right;
151 if (temp.right != null) {
152 // 该结点可能不存在
153 temp.right.parent = node;
154 }
155
156 temp.right = node;
157 node.parent = temp;
158
159 // 旋转完成.修正根结点与父结点
160 // 1.node为根结点
161 if (node == root) {
162 root = temp;
163 temp.parent = null;
164 return;
165 }
166
167 // 2.node不为根结点
168 // node 为父结点的右孩子
169 if (node == p.right) {
170 p.right = temp;
171 } else {
172 p.left = temp;
173 }
174 temp.parent = p;
175 }
176
177 // 中序遍历
178 public void infixOrder() {
179 this.infixOrder(root);
180 }
181
182 private void infixOrder(RBNode root) {
183 if (root != null) {
184 this.infixOrder(root.left);
185 System.out.print("-->" + root.value + ":" + (root.red ? "红" : "黑"));
186 this.infixOrder(root.right);
187 }
188 }
189
190 /**
191 * 红黑树 树结点结构
192 */
193 protected static class RBNodeextends Comparable> {
194 private T value;
195 // 默认为 红色 结点
196 private boolean red = true;
197
198 private RBNode left;
199 private RBNode right;
200 private RBNode parent;
201
202 public RBNode() {
203 }
204
205 public RBNode(T value) {
206 this.value = value;
207 }
208
209 // 返回结点的度
210 public int getDegree() {
211 if (this.left == null && this.right == null) {
212 return 0;
213 }
214
215 if ((this.left != null && this.right == null) || (this.left == null && this.right != null)) {
216 return 1;
217 }
218
219 return 2;
220 }
221
222 public RBNode getUncle() {
223 final RBNode grandFather = this.parent.parent;
224 final RBNode parent = this.parent;
225
226 if (parent == grandFather.left) {
227 return grandFather.right;
228 }
229
230 if (parent == grandFather.right) {
231 return grandFather.left;
232 }
233
234 return null;
235 }
236
237 public RBNode getGrandFather() {
238 return this.parent.parent;
239 }
240
241 @Override
242 public String toString() {
243 return "RBNode{" +
244 "value=" + value +
245 ", red=" + red +
246 '}';
247 }
248 }
249 }
完整的红黑树插入代码
代码示例:测试
1 public class Main {
2 public static void main(String[] args) {
3 Integer[] integers = {15, 7, 45, 3, 10, 25, 55, 1, 5, 75};
4 RBTree tree = new RBTree<>(integers);
5
6 tree.infixOrder();
7 }
8 }
9
10 // 结果
11 -->1:红-->3:黑-->5:红-->7:红-->10:黑-->15:黑-->25:黑-->45:红-->55:黑-->75:红
最后,推荐一个在线构建红黑树的地址:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html 用于读者验证上述代码的结果。上述测试案例构建的红黑树为:
返回顶部## 三、删除
见下一篇。