Yolov5之矩形推理

前言

在Yolov5项目中，矩形推理是一种重要的技巧，减少了数据的冗余信息，可以在几乎没有精度损失的情况下，加快模型推理的速度。
在本文中，我将对矩推理的原理以及源码部分进行介绍，以及我个人以前在学习过程中的一些思考，其实原理不难，主要就是把整个思路梳理清楚。

一，图像预处理之resize

在讲矩形推理之前，我们先来看看rezise操作，也就是对图片进行缩放。我们都知道，在模型推理前，一般需要对原始图片进行预处理，预处理中最重要的一个步骤就是resize，也就是将原始图片尺寸调整为统一大小的推理尺寸，一般会调整到宽高相等的尺寸。

而在平面几何中，矩形一般有邻边相等和不相等两种情况，图片也一样，有宽高相等和不相等的图片。因此我们在resize的过程中，也需要考虑两种情况，即将宽高相等和宽高不相等的图片resize成宽高相等的图片，然后再进行推理。

听起来是不是很拗口，其实用一句话就可以概括：
对图片进行相等比例缩放和不等比例缩放。
那这两种情况有什么不一样的地方呢？让我们接着往下看。

情况一：对图片进行相等比例缩放

对于本来宽高就相等的原始图片，直接resize成宽高相等的尺寸当然可以，resize后的图片尺寸大小变了，但是宽高肯定还是相等的，宽高比不变，即对图片进行了等比例缩放，此时图片不发生形变；

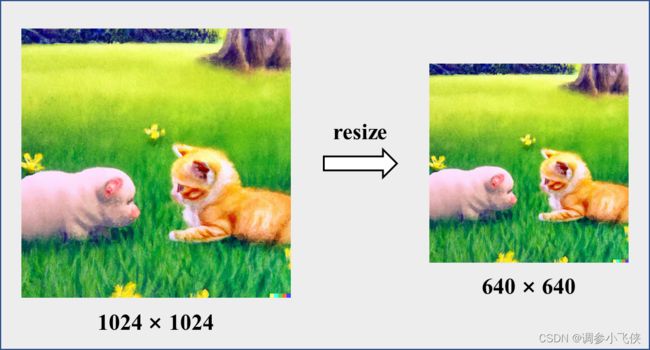
情况二：对图片进行不等比例缩放

对于宽高不相等的原始图片，直接resize成宽高相等的尺寸，这时候图片的宽高比变了，即对图片进行了不等比例缩放，就会导致图片变形，图片变形会导致图片的特征信息发生改变，甚至会丢失特征信息，导致图片失真，最终影响模型的识别精度。

那对于以上情况，我们怎么能将宽高不相等的图片进行等比例缩放，并且resize为宽高相等的图片呢？话不多说，直接上图。

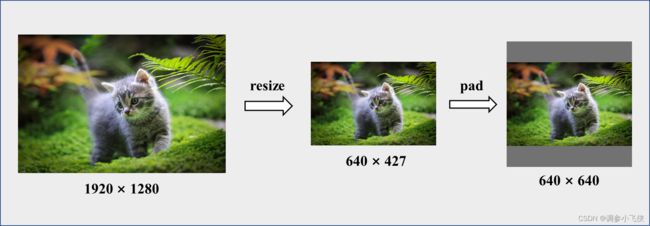
从图中我们可以看出，首先我们要保证resize后图片宽高比和原始图片一致，再通过像素填充让宽高相等，这样就可以保证图片不发生形变，是不是很简单。
该方法就是针对情况二造成的变形问题进行的改进，而对于宽高相等的图片因为不存在变形问题，则rezise后就不需要进行像素填充了。

二，为什么要采用矩形推理？

通过上面的方法，我们已经可以做到在保证图片不变形的情况下将任何形状的图片resize成我们想要的尺寸，那这样的方法，优点就是保证了图片不变形，那它有没有缺点呢？换句话说，还有改进的空间吗？答案自然是肯定的。
可能已经有人想到了，我们推理的时候一定要用宽高相等的图片吗？答案是不一定的。
模型会对输入图片进行下采样，而下采样的步长通常设置为2的整数倍，yolov5的下采样步长为2，经过了5次下采样，最终下采样了32倍，所以只要保证宽高是32的最小整数倍即可。

从上图来看，我们等比例缩放并填充像素后已经得到了宽高相等的图片，图片尺寸为640×640。上面已经讲到，我们只需要保证宽高为32的倍数即可，不需要一定是宽高相等。也就是说我们在填充像素的时候其实可以不需要填充到宽高相等，只要填充到32的最小整数倍即可。这样做的目的就是为了减少图像的冗余信息，也加快了推理的速度。
矩形推理的大致流程如下：
step1：对原始图片进行等比例缩放
step2：对短边进行像素填充，填充到32的最小整数倍

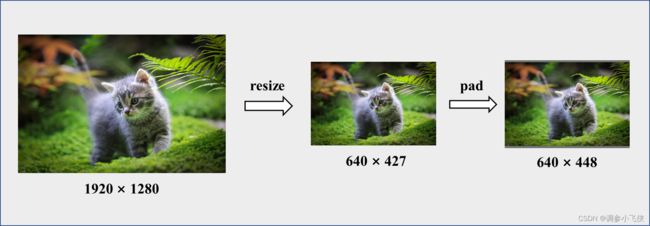
三，源码分析

yolov5对图片进行resize的函数为letterbox函数，在utils/augmentations.py代码中。

参数解析：
1，im：输入的原始图像，numpy数组格式
2，new_shape：resize后的图像尺寸
3，color：填充像素的颜色
4，auto：最小矩形填充开关，默认为True
5，scale_Fill：直接进行resize，默认为False
6，scale_up：只缩小，不放大，默认为True
7，stride：矩形填充的缩放公因数，默认为32

def letterbox(im, new_shape=(640, 640), color=(114, 114, 114), auto=True, scaleFill=False, scaleup=True, stride=32):
    # Resize and pad image while meeting stride-multiple constraints
    shape = im.shape[:2]  # 获取原始图像的尺寸
    if isinstance(new_shape, int):  # 判断new_shape是否为整数
        new_shape = (new_shape, new_shape)  # 是整数则将new_shape转换为二维元组

    # 计算缩放系数 (new / old)
    r = min(new_shape[0] / shape[0], new_shape[1] / shape[1])  # 取最小值                          
    if not scaleup:  # 只缩小不放大操作，可在验证时得到更好的map
        r = min(r, 1.0)  # 大于1缩放系数取1，小于1缩放系数取r，可做到不放大图像

    # 计算pad
    ratio = r, r  # 宽高的缩放比例，保持一致
    new_unpad = int(round(shape[1] * r)), int(round(shape[0] * r))  # 计算缩放后的宽高
    dw, dh = new_shape[1] - new_unpad[0], new_shape[0] - new_unpad[1]  # 计算缩放后宽高需要填充到new_shape的像素大小
    if auto:  # 最小矩形填充，默认开启
    	# 计算填充到最小矩形需要的像素大小
        dw, dh = np.mod(dw, stride), np.mod(dh, stride)  # wh padding
    elif scaleFill:  # 直接resize，不考虑形变，默认关闭
        dw, dh = 0.0, 0.0  # 不进行填充
        new_unpad = (new_shape[1], new_shape[0])  # 直接resize为new_unpad 
        ratio = new_shape[1] / shape[1], new_shape[0] / shape[0]  # 缩放比例直接用原始宽高除以新的宽高得到
	
	# 填充的像素大小需要除以2，因为是上下左右对称填充
    dw /= 2
    dh /= 2

    if shape[::-1] != new_unpad:  # 开始进行resize
        im = cv2.resize(im, new_unpad, interpolation=cv2.INTER_LINEAR)  # 双线性插值
    top, bottom = int(round(dh - 0.1)), int(round(dh + 0.1))  # 上下填充的像素大小
    left, right = int(round(dw - 0.1)), int(round(dw + 0.1))  # 左右填充的像素大小
    im = cv2.copyMakeBorder(im, top, bottom, left, right, cv2.BORDER_CONSTANT, value=color)  # 边缘填充
    return im, ratio, (dw, dh)

可能有部分内容讲的不是特别清楚，若有问题欢迎在评论区留言指正！