二叉树的顺序存储——堆——初识堆排序

前面我们学过可以把完全二叉树存入到顺序表中，然后利用完全二叉树的情缘关系，就可以通过数组下标来联系。

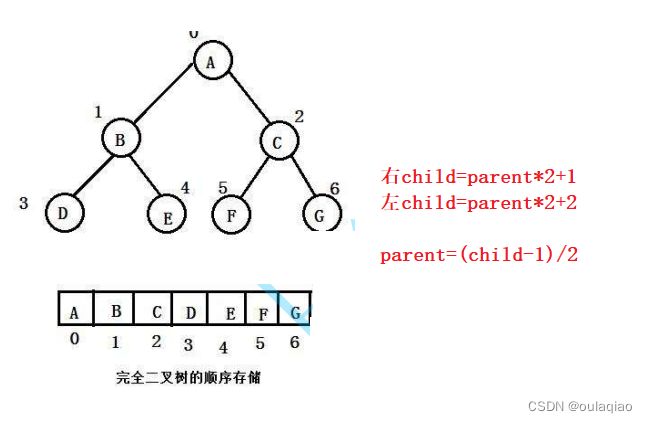
但是并不是把二叉树存入到数组中就是堆了，要看原原来的二叉树是否满足：所有的父都小于等于子，或者所有的父都大于等于子——既小堆大堆

现在我们用代码来实现数据存入到顺序表中，并且是小堆
首先需要创建一个顺序表的结构体

然后初始化

void HeapInit(Heap* php)//初始化
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}

放入数据
首先要用指针开辟一块空间并判断是否需要扩容，然后把数据尾插进去

void HeapPush(Heap* php, HpDatatype x)//放入数据
{
	assert(php);
	//扩容
	if (php->capacity == php->size)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HpDatatype* tmp = (HpDatatype*)realloc(php->a, sizeof(HpDatatype)*newcapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;
	Adjust(php->a, php->size - 1);//调整
}

但是因为这个数组要满足小堆，所以尾插进去的数还需要进一步的调整

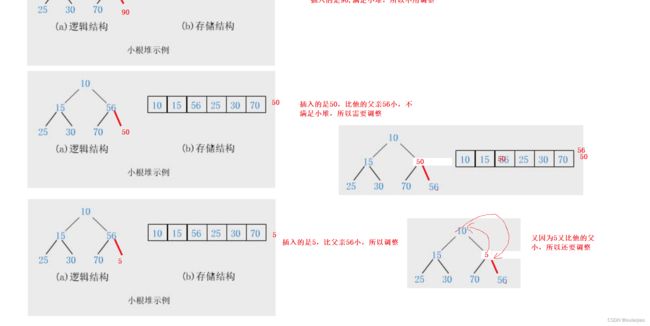
那么这里的代码是如何实现的呢

到这里的时候我们没插入一个数据就都可以把数据从新调整为一个堆，那么我们为什么要把数据按照堆的方式存储呢？
现在我们来写一个堆数据删除的代码就能感受到堆的作用：

void AdiustDown(HpDatatype* a, int n, int parent)
{
	int child = parent * 2 + 1;//先假设和根交换的是他的左儿子
	while (child<n)//当child=parent*2+1已经超出了数组的范围，那么就说明他下面已经没有儿子了，此时也是结束循环
	{
		if (child+1<n && a[child + 1] < a[child])//如果假设错误，那么就换成右儿子，但是这里要注意的child+1（右儿子）存在
		{
			child++;
		}
		if (a[child] < a[parent])//判断是否需要换
		{
			Swap(&a[child], &a[parent]);//交换
			//尾下一次循环做准备
			parent = child;
			child = parent * 2 + 1;
		}
		else//如果不用换就直接跳出循环
		{
			break;
		}
	}
}

void HeapPop(Heap* php)//删除根
{
	assert(php);
	assert(php->size>0);
	Swap(&php->a[0], &php->a[php->size - 1]);//交换
	php->size--;//尾删
	//向下调整
	 AdiustDown(php->a, php->size, 0);


}

有了这个删根代码，我们在加上取根代码，和判空代码，便可实现数据的排序打印

HpDatatype  HeapTop(Heap* php)//返回根值
{
	assert(php);
	assert(php->size > 0);

	return php->a[0];
}

bool HeapEmpty(Heap* php)//判空
{
	assert(php);
	return php->size==0;
}

while (!HeapEmpty(&st))
	{
		printf("%d ", HeapTop(&st));//打印顶值
			HeapPop(&st);
	}

如果把上面插入数据和删除根向下调整的判断语句的小于改成大于那么就实现了打印出来的数据时从大到小的排序

这里就体现出了堆的魅力，当一组数据时以堆的形式储存的，那么他在排序的时候的时间复杂度就是
O(logN^{2),而之前我们学习的冒泡排序的时间复杂度是O(N}2),显然堆的排序时间复杂度更低

但是这里平不是用堆来排序的实际用法，因为如果给我们一个数组，进行排序，我们是要实际改变数组里面值的位置，并不是像这里这样pop一次然后取根打印出来，即使我们每次用取出来的根值去覆盖原来的数组，那么我们要用这样的堆就需要写上面所以的建立堆的数据结构代码，显然是太麻烦了。

那么我们是否可以：

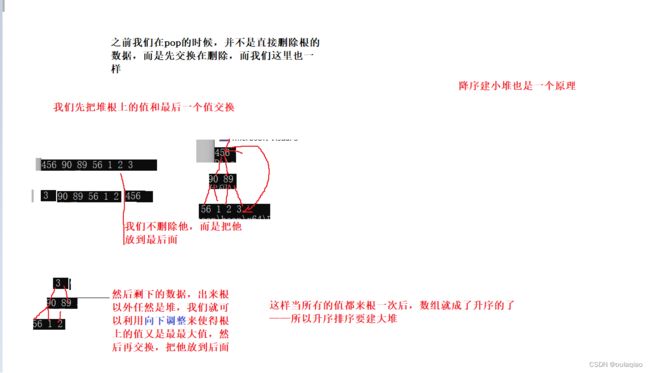
把给的数组变成堆的时候我们就要进行排序，因为这里并没有上面写的数据结构的堆，所以我们无法取根然后再打印，——之前也说了这种方法是不会把原本的数组改变成有有序的，

所以之下要讲的才是如何在把一个数组已经变成堆的情况下进行排序：

降序排序-——恰恰是把数组变成大堆，升序排序恰恰是把数组变成小堆
为什么要这样呢？

升序代码：

#include
#include
#include
#include

void Swap(int* child, int* parent)//交换
{
	int temp = *child;
	*child = *parent;
	*parent = temp;
}

Adjust(int* a, int child)//向上调整形成堆
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[parent] < a[child])
		{
			Swap(&a[parent], &a[child]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

AdiustDown(int* a, int n, int parent)//向下调整
{
	int child = parent * 2 + 1;
	while (child<n)
	{
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			Swap(&a[child],&a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
		
	}
}
int main()
{
int arr[] = { 90,56,3,46,1,2,89 };
int n = sizeof(arr) / sizeof(int);
for (int i = 1; i < n; i++)
{
	Adjust(arr, i);//调整
}
int end = n - 1;//最后一个数的下标
while (end > 0)
{
	Swap(&arr[0], &arr[end]);
	//向下调整
	AdiustDown(arr, end, 0);
	end--;
}



for (int j = 0; j < n; j++)
{
	printf("%d ", arr[j]);
}

return 0;
}