计算机组成原理期末复习

第一章

1. 上机前的准备：建立数学模型、确定计算方法和编制解题程序
2. n位操作码有$2^n$种不同操作
3. 主储存器（主存/内存）包括存储体M、各种逻辑部件及控制电路。储存体有多个储存单元，储存单元有多个储存元件，每个存储元件寄存一个2进制码。一个储存字是一个储存单元存储的二进制代码串，代码串的长度（位数）为存储字长。

第二章

1. IAS 计算机的总体结构它由几部分组成：一个同时存放指令和数据的主存储器、一个二进制的算逻运算部件、一个解释存储器中的指令并能控制指令执行的程序控制部件以及由控制部件操作的I/0设备。
2. 晶体管特点：小体积、低耗电以及载流子高速运行

第三章

1. 计算机系统的五大部件之问的互连方式有两种，一种是各部件之问使用单独的连线，称为分
   散连接;另一种是将各部件连到一组公共信息传输线上，称为总线连接。
2. 早期计算机以运算器为中心，采用分散连接方式，后改进为以存储器为中心
3. 总线由诸多传输线或通路组成，n条传输线可以同时传输n位二进制代码
4. 存储总线(M 总线)连接 CPU 和主存;输人输出总线(I/O总线)用来建立CPU和各I/O设
   备之间交换信息的通道。
5. 系统总线(板级总线/板间总线)是指CPU、主存、I/O设备(通过I/O接口)各大部件之间的信息传输线，按传输信息不同分为：数据总线、地址总线和控制总线。
6. 数据总线是衡量系统性能的一个重要参数，双向传输。系统总线宽度(位数)为n位，指令字长位m位，则CPU取指阶段需要访问$\frac{m}{n}$(向上取整)次主存。
7. 地址总线用来指出数据总线上源数据或目的数据在主存单元的地址或I/O设备的地址，由CPU输出，单向传输。地址线为n根，则对应的存储单元个数为$2^n$。
8. 控制总线用来发出各种控制信号，对任一控制线通常单向传输，但控制总线整体双向传输。常见的控制信号：
   1. 时钟：用来同步各种操作。
   2. 复位：初始化所有部件。
   3. 总线请求：表示某部件需获得总线使用权。
   4. 总线允许：表示需要获得总线使用权的部件已获得了控制权。
   5. 中断请求：表示某部件提出中断请求。
   6. 中断响应：表示中断请求已被接收。
   7. 存储器写：将数据总线上的数据写至存储器的指定地址单元内。
   8. 存储器读：将指定存储单元中的数据读到数据总线上。
   9. I/O读：从指定的I/O 端口将数据读到数据总线上。
   10. I/O写：将数据总线上的数据输出到指定的I/O 端口内。
   11. 传输响应：表示数据已被接收，或已将数据送至数据总线上
9. 总线传输周期是连接在总线上的两个部件完成一次完整且可靠的信息传输时间，包含4个时钟周期$T_1、T_2、T_3、T_4$
10. CPU在T₁上升沿发出地址信息;在T₂的上升沿发出读命令;与地址信号相符合的输人设备按命令进行一系列内部操作,且必须在T₃的上升沿到来之前将CPU所需的数据送到数据总线上;CPU在T₃时钟周期内,将数据线上的信息送到其内部寄存器中;CPU在T₄的上升沿撤销读命令,输人设备不再向数据总线上传送数据，撤销它对数据总线的驱动。如果总线采用三态驱动电路,则从T₄起,数据总线呈浮空状态。
11. 对于读命令，其传输周期如下：T₁主模块发地址。T₂主模块发读命令。T₃从模块提供数据。T₄主模块撤销读命令,从模块撤销数据。
12. 对于写命令，其传输周期如下：T₁主模块发地址。T₂主模块提供数据。T₃主模块发出写命令，从模块按收到命令后，必须在规定时间内将数据总线上的数据写到地址总线所指明的单元中T₄主模块撤销写命令和数据等信号。

第四章

1. 存储器存放数据和程序，

   1. 按介质分类为：
      1. 半导体存储器，其由半导体器件组成，体积小、功耗低、存取时间短，但断电丢失，易失性存储器，可按材料再分为双极性（TTL）半导体存储器（快速）和MOS半导体存储器（高集成度、制造简单、成本低廉、功耗低、使用广泛）
      2. 磁表面存储器，非易失性，按载磁体不同分为磁盘、磁带、磁鼓
      3. 磁芯存储器，体积大、工艺复杂、功耗大，不易失的永久记忆存储器
      4. 光盘存储器非易失性、记录密度高、耐用性好、可靠性高、可互换性强
   2. 按存取方式分类：
      1. 随机存储器RAM：随机存取，存储信息原理不同分为静态ROM（以触发器原理寄存信息）和动态ROM（以电容充放电原理寄存信息）
      2. 只读存储器ROM：只能读出不能写入
      3. 串行访问存储器
   3. 按在计算器中的作用分类：
      1. 主存储器（和CPU直接交换信息）：速度快、容量小、价格高
      2. 辅助存储器（存放暂时不用的程序和数据）：速度慢、容量大、价格低
      3. 缓冲存储器（用在两个速度不同的部件中，起缓冲作用）
         即$$存储器=\{\begin{array}{l}主存\{\begin{array}{l}随机存储器（RAM）\{\begin{array}{l}静态RAM\\ 动态RAM\end{array}\\ 只读存储器（ROM）\{\begin{array}{l}MROM\\ PROM\\ EPROM\\ EEPROM\end{array}\end{array}\\ 闪速存储器（FlashMemory）\\ 辅存\{\begin{array}{l}磁盘\\ 磁带\\ 光盘\end{array}\\ 缓存（Cache）\end{array}$$

2. 解释概念:
   主存:主存储器,用于存放正在执行的程序和数据。 CPU 可以直接进行随机读写,访问速度较高。
   辅存:辅助存储器,用于存放当前暂不执行的程序和数据,以及一些需要永久保存的信息。
   Cache :高速缓冲存储器,介于 CPU 和主存之间,用于解决 CPU 和主存之间速度不匹配问题。
   RAM :半导体随机存取存储器,主要用作计算机中的主存。
   SRAM :静态半导体随机存取存储器。
   DRAM:动态半导体随机存取存储器。
   ROM:掩膜式半导体只读存储器。由芯片制造商在制造时写入内容,以后只能读出而不能写入。
   PROM:可编程只读存储器,由用户根据需要确定写入内容,只能写入一次。
   EPROM :可擦除可编程只读存储器。允许用户写入信息，之后用某种方法擦除数据，可进行多次重写。
   EEPROM :电擦写可编程只读存储器。
   CDROM:只读型光盘。
   Flash Memory :闪速存储器。或称快擦型存储器。

3. 存取周期和存取时间的区别：存取周期和存取时间的主要区别是：存取时间仅为完成一次操作的时间，而存取周期不仅包含操作时间，还包含操作后线路的恢复时间。即：存取周期=存取时间+恢复时间

4. 存储器的带宽指单位时间内从存储器进出信息的最大数量。若存储器的数据总线宽度为32位，存取周期为200ns，则存储器的带宽= 1/200ns ×32位 = 160M位/秒 = 20MB/秒 = 5M字/秒。注:字长32位,不是16位。(注:1ns=10⁻⁹s)

5. 刷新:对 DRAM 定期进行的全部重写过程;刷新原因:因电容泄漏而引起的 DRAM 所存信息的衰减需要及时补充,因此安排了定期刷新操作;常用的刷新方法有三种:

   1. 集中式:在最大刷新间隔时间内,集中安排一段时间进行刷新,存在 CPU 访存死时间。
   2. 分散式:在每个读 /写周期之后插入一个刷新周期,无 CPU 访存死时间。
   3. 异步式:是集中式和分散式的折衷。

6. 计算机中设置 Cache 的作用是解决 CPU 和主存速度不匹配问题。不能将 Cache 的容量扩大取代主存，原因是

   1. Cache 容量越大成本越高，难以满足人们追求低价格的要求；
   2. 如果取消主存，当 CPU 访问 Cache 失败时，需要将辅存的内容调入 Cache 再由 CPU 访问，造成 CPU 等待时间太长，损失更大。

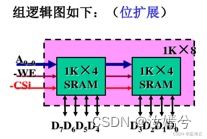
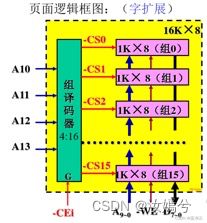
7. 画出用1024×4位的存储芯片组成一个容量为64Kx8位的存储器逻辑框图。要求将64K分成4个页面,每个页面分16组,共需多少片存储芯片?
   设采用SRAM芯片，则：总片数=（64K×8位）/（1024×4位）=64×2=128片
   题意分析：本题设计的存储器结构上分为总体、页面、组三级，因此画图时也应分三级画。
   首先应确定各级的容量：
   ​ 页面容量=总容量/页面数=64K×8/4=16K×8位，4片16K×8字串联成64K×8位
   ​ 组容量=页面容量/组数=16K×8位/16=1K×8位，16片1K×8位字串联成16K×8位
   ​ 组内片数=组容量/片容量=1K×8位/1K×4位=2片，两片1K×4位芯片位并联1K×8位
   ​ 地址分配

   
   
   

8. 设有一个64K$\times$8位的RAM芯片,试问该芯片共有多少个基本单元电路(简称存储基元)?欲设计一种具有上述同样多存储基元的芯片,要求对芯片字长的选择应满足地址线和数据线的总和为最小,试确定这种芯片的地址线和数据线，并说明有几种解答。存储基元总数=64K$\times$8位=512K位=2¹⁹位
   如要满足地址线和数据线总和最小,应尽量把存储元安排在字向,因为地址位数和字数成2的幂的关系,可较好地压缩线数。
   设地址线根数为a,数据线根数为b,则片容量为:2^a×b=2¹⁹;b=2¹⁹−a;
   若a=19,b=1,总和=19+1=20;
   a=18,b=2,总和=18+2=20;
   a=17,b=4,总和=17+4=21;
   a=16,b=8 总和=16+8=24;

9. 某8位微型计算机地址码为18位,若使用4K×4位的RAM芯片组成模块板结构的存储器,试问：

   1. 该机所允许的最大主存空间是$2^{18}\times 8位=245K\times 8位=256KB$
   2. 若每个模块板为32K×8位，共需模块板总数 = $$(256K\times 8)÷(32K\times 8)=8$$块
   3. 每个模块板内共有板内片数 = $(32K\times 8位)÷(4K\times 4位)=8\times 2=16$片
   4. 共有RAM总片数 = $$16片\times 8=128$$片
   5. CPU选择各模块板：CPU通过最高3位地址译码输出选择模板,次高3位地址译码输出选择芯片。地址格式分配如下:

   模板号(3位)	芯片号(3位)	片内地址(12位)

10. 欲传送的二进制代码为1001101,用奇校验来确定其对应的汉明码,若在第6位出错,说明纠错过程。
    ​ 欲传送的二进制代码为1001101，有效信息位数为n=7位，则汉明校验的校验位为k位，则：2^k ≥ n + k + 1，k = 4，进行奇校验设校验位为 C₁ C₂C₄C₈，汉明码为 C₁C₂b₇C₄b₆b₅b₄C₈b₃b₂b₁，

    序号	1	2	3	4	5	6	7	8	9	10	11
    名称	C1	C2	b7	C4	b6	b5	b4	C8	b3	b2	b1

    $$C_1=\overline{b_7⨁b_6⨁b_4⨁b_3⨁b_1}=\overline{1⨁0⨁1⨁1⨁1}=1$$
    $$C_2=\overline{b_7⨁b_5⨁b_4⨁b_2⨁b_1}=\overline{1⨁0⨁1⨁0⨁1}=0$$
    $$C_4=\overline{b_6⨁b_5⨁b_4}=\overline{0⨁0⨁1}=0$$
    $$C_8=\overline{b_3⨁b_2⨁b_1}=\overline{1⨁0⨁1}=0$$
    故传送的汉明码为10100011101，若第6位(b₅)出错，即接收的码字为10100111101，则
    $$P_1=\overline{C_1⨁b_7⨁b_6⨁b_4⨁b_3⨁b_1}=\overline{1⨁1⨁0⨁1⨁1⨁1}=1$$
    $$P_2=\overline{C_2⨁b_7⨁b_5⨁b_4⨁b_2⨁b_1}=\overline{0⨁1⨁1⨁1⨁0⨁1}=1$$
    $$P_4=\overline{C_4⨁b_6⨁b_5⨁b_4}=\overline{0⨁0⨁1⨁1}=1$$
    $$P_8=\overline{C_8⨁b_3⨁b_2⨁b_1}=\overline{1⨁1⨁0⨁1}=0$$
    P₈P₄P₂P₁=0110说明第6位出错，对第六位取反即完成纠错。

第五章

1. I/O通道用来负责管理I/O设备以及实现主存与I/O设备之间交换信息，提高CPU的资源利用率。
2. I/O处理机提高CPU的并行性
3. I/O指令的一般格式：操作码｜命令码｜设备码
4. I/O处理中断的过程：中断请求、中断判优、中断响应、中断服务和中断返回。
5. 以键盘设备为例，结合图说明I/O中断处理的全过程。当CPU通过I/O指令的地址码选中某设备后。则：
   1. 由CPU发启动I/O设备命令，将接口中的B置“1”，D置“0”;
   2. 接口启动输入设备开始工作;
   3. 输入设备将数据送入数据缓冲寄存器;
   4. 输入设备向接口发出“设备工作结束”信号，将D置“1”，B置“0”，标志设备准备就绪;
   5. 当设备准备就绪(D=1)。且本设备未被屏蔽(MASK=0)时，在指令执行阶段的结束时刻，由CPU发出中断查询信号;
   6. 设备中断请求触发器INTR 被置“1”，标志设备向CPU提出中断请求。与此同时，INTR送至排队器,进行中断判优;
   7. 若CPU允许中(EINT=1)，设备又被排队选中，即进入中断响应阶段，由中断响应信号INTA 将队器输出送至编码器形成向量地址;
   8. 向量地址送至PC，作为下一条指令的地址;
   9. 由于向量地址中存放的是一条无条件转移指令，故这条指令执行结束后，即无条件转至该设备的服务程序入口地址，开始执行中断服务程序，进入中断服务阶段，通过输入指令将数据缓冲寄存器的输入数据送至 CPU的通用寄存器，再存入主存相关单元;
   10. 中服务程序的最后一条指令是中断返回指令，当其执行结束时，即中断返回至原程序的断点处。至此，一个完整的程序中断处理过程即告结束。
6. 中断服务程序的流程：保护现场、中断服务、回复现场、中断返回
7. 程序查询方式和程序中断方式都是通过“程序”传送数据,两者的区别是什么?
   • 程序查询方式是用户在程序中安排一段输入输出程序，它由I/O 指令、测试指令和转移指令等组成。CPU一旦启动 I/O 后，就进入这段程序，时刻查询 I/O 准备的情况，若未准备就绪就踏步等待；若准备就绪就实现传送。在输入输出的全部过程中，CPU 停止自身操作。
   • 程序中断方式虽也要用程序实现外部设备的输入输出，但它只是以中断服务程序的形式插入到用户现行程序中。即 CPU 启动 I/O 后，继续自身的工作，不必查询 I/O 的状态。而 I/O 被启动后，便进入自身的准备阶段，当其准备就绪时，向 CPU 提出中断请求，此时若满足条件，CPU 暂停现行程序，转入该设备的中断服务程序，在服务程序中实现数据的传送。
8. 调用中断服务程序和调用子程序有何区别?
9. 子程序的执行是程序员事先安排好的（由调用子程序的指令转入）；中断服务程序的执行一般由随机的中断事件引发。
10. 子程序的执行受到主程序或上层子程序的控制；中断服务程序一般与被中断的现行程序无关。
11. 不存在同时调用多个子程序的情况，因此子程序不需要进行优先级排队；而不同中断源则可能同时向CPU 提出服务请求，因此需要中断仲裁及优先级排队。
12. 子程序是由调用指令给出目标地址，中断是通过隐指令获得中断服务程序的入口地址。

第六章

1. $$浮点数N=S\times r^j(阶码数值位m位，位数数值位n位)=\{\begin{array}{l}阶码j\{\begin{array}{l}阶符j_f\\ 阶码的数值部分j_1{j}_2\cdot \cdot \cdot j_m（m反映浮点数的表示范围）\end{array}\\ （小数点的实际位置：由j_f和m共同表示）\\ 尾数S\{\begin{array}{l}数符S_f（浮点数的符号）\\ 阶码的数值部分S_1{S}_2\cdot \cdot \cdot S_n（n反映浮点数的精度）\end{array}\end{array}$$
   $$最大正数2^{(2^m-1)}\times (1-2^{-n});最小正数2^{-(2^m-1)}\times 2^{-n};最大负数-2^{-(2^m-1)}\times 2^{-n};最小负数-2^{(2^m-1)}\times (1-2^{-n})$$
   上溢：浮点数阶码超出最大阶码，停止运算，进行中断溢出处理
   下溢：浮点数阶码小于最小阶码，尾数位强制为零，按机器零处理。

2. 规格化数：小数最高位为1，且整体小于1
   e.g. 设机器数字长为24位，欲表示$\pm$3万的十进制数，试问在保证数的最大精度的前提下，除阶符、数符各取一位外，阶码、尾数各取几位？
   KaTeX parse error: No such environment: flalign* at position 7: \begin{̲f̲l̲a̲l̲i̲g̲n̲*̲}̲ &\because 2^{1…

3. 算术移位：有符号数的移位；逻辑移位：无符号数的移位。

4. 逻辑移位规则：

   1. 左移：高位移丢，低位添0
   2. 右移：低位移丢，高位添0

5. 设机器数字长为8位（含1位符号位），若A=+15，B=+24，求[A-B]_补并还原成真值。
   $$\because A=+15=+0001111,B=+24=+0011000$$
   $$\therefore [A{]}_{补}=0,0001111,[B{]}_{补}=0,0011000,[-B{]}_{补}=1,1101000$$
   则[A-B]_补=[A]_补+[-B]_补=$$\begin{array}{r}0,0001111\\ +1,1101000\\ 1,1110111\end{array}$$
   $\therefore$[A-B]_补=1,111 0111
   $\therefore$A-B=-0001001=-9

6. 已知[x]_补=1.0101，[y]_补=0.1101，[x·y]_补。

   部份积	乘数	说明
   $\begin{array}{r}00.0000\\ +11.0101\end{array}$	$\begin{array}{r}110\underline{1}\\ 0000\end{array}$	$$\begin{gathered} 初值[z_0{]}_{补}=0 \\ {y}_4=1，+[x{]}_{补} \end{gathered}$$
   $\begin{array}{r}11.0101\\ 11.1010\\ 11.1101\\ +11.0101\end{array}$	$\begin{array}{r}0000\\ 111\underline{0}\\ 011\underline{1}\\ 0000\end{array}$	$ \rightarrow1位，得[z_1]_补，乘数同时\rightarrow1位\ y_3=0，\rightarrow1位，得[z_2]_补，乘数同时\rightarrow1位\y_2=1\+[x]_补$
   $\begin{array}{r}11.0010\\ 11.1001\\ +11.0101\end{array}$	$\begin{array}{r}0100\\ 001\underline{1}\\ 0000\end{array}$	$$\begin{gathered} \to 1位，得[z_3{]}_{补}，乘数同时\to 1位 \\ {y}_1=1 \\ +[x{]}_{补} \end{gathered}$$
   $\begin{array}{r}10.1110\\ 11.0111\end{array}$	$\begin{array}{r}0010\\ 0001\end{array}$	$$\begin{gathered} \to 1位 \\ 得[z_4{]}_{补} \end{gathered}$$
   故乘积[x·y]补=1.0111 0001

7. 设机器数字长为8位(含1位符号位)，用补码运算规则计算下列各题

   1. $A=\frac{9}{64}，B=-\frac{13}{32}，求A+B$

   $$\begin{gathered} A=\frac{9}{64}=(0.0010010{)}_2 \\ B=-\frac{13}{32}=(-0.0110100{)}_2 \\ [A{]}_{补}=0.0010010 \\ [B{]}_{补}=1.1001100 \\ [A+B{]}_{补}=\begin{array}{r}0.0010010\\ +1.1001100\\ 1.1011110\end{array}(无溢出) \\ A+B=(-0.0100010{)}_2=-\frac{17}{64} \end{gathered}$$

   2. $A=\frac{19}{32}，B=-\frac{17}{128}，求A-B$

   $$\begin{gathered} A=\frac{19}{32}=(0.1001100{)}_2 \\ B=-\frac{17}{128}=(-0.0010001{)}_2 \\ [A{]}_{补}=0.1001100 \\ [B{]}_{补}=1.1101111 \\ [-B{]}_{补}=0.0010001 \\ [A-B{]}_{补}=\begin{array}{r}0.1001100\\ +0.0010001\\ 0.1011101\end{array}(无溢出) \\ A-B=(0.1011101{)}_2=\frac{93}{128} \end{gathered}$$

   3. $A=-\frac{3}{16}，B=\frac{9}{32}，求A+B$

   $$\begin{gathered} A=-\frac{3}{16}=(-0.0011000{)}_2 \\ B=\frac{9}{32}=(0.0100100{)}_2 \\ [A{]}_{补}=1.1101000 \\ [B{]}_{补}=0.0100100 \\ [A+B{]}_{补}=\begin{array}{r}1.1101000\\ +0.0100100\\ 0.001100\end{array}(无溢出) \\ A+B=(0.0001100{)}_2=\frac{3}{32} \end{gathered}$$

   4. $A=-87，B=53，求A-B$

   $$\begin{gathered} A=-87=(-1010111{)}_2 \\ B=53=(110101{)}_2 \\ [A{]}_{补}=1,0101001 \\ [B{]}_{补}=0,0110101 \\ [-B{]}_{补}=1,1001011 \\ [A-B{]}_{补}=\begin{array}{r}1,0101001\\ +1.1001011\\ 0,1110100\end{array}(溢出) \\ A-B=(-1,0001100{)}_2=-140 \end{gathered}$$

   5. $A=115，B=-24，求A+B$

   $$\begin{gathered} A=115=(1110011{)}_2 \\ B=-24=(-11000{)}_2 \\ [A{]}_{补}=0,1110011 \\ [B{]}_{补}=1,1101000 \\ [A+B{]}_{补}=\begin{array}{r}0,1110011\\ +1,1101000\\ 0,1011011\end{array}(无溢出) \\ A+B=(1011011{)}_2=91 \end{gathered}$$

第七章

1. RISC即精简指令系统计算机（Reduced Instruction Set Computer），与其对应的是 CISC，即复杂指令系统计算机（Complex Instruction Set Computer）。人们从80-20规律中得到启示；仅用最常用的20%的简单指令，重新组合不常用的 80%的指令功能，这便引发出RISC技术。所以，RISC 指令系统就是通过简化指令，复杂指令的功能由执行频度高的简单指令组合来实现。
   RISC 的主要特点：
   1. 选取使用频度较高的一些简单指令以及一些很有用但又不复杂的指令，让复杂指令的功能由频度高的简单指令的组合来实现；
   2. 指令长度固定，指令格式种类少，寻址方式种类少；
   3. 只有取数/存数 (LOAD\ STORE) 指令访问存储器，其余指令的操作都在寄存器内完成；
   4. CPU 中有多个通用寄存器；
   5. 采用流水线技术，大部分指令在一个时钟周期内完成。采用超标量和超流水线技术，可使每条指令的平均执行时间小于一个时钟周期；
   6. 控制器采用组合逻辑控制，不用微程序控制。
   7. 采用优化的编译程序。
2. RISC 机中指令简单,有些常用的指令未被选用,它用什么方式来实现这些常用指令的功能.试举例说明。
   RISC机不仅精简了指令系统，采用超标量和超流水线结构；它们的指令数目只有几十条，却大大增强了并行处理能力。RISC 机中指令简单,有些常用的指令未被选用,它选取使用频度较高的一些功能简单、能在一个节拍内执行完成的指令来实现这些常用指令的功能，而把较复杂的功能用频度高的简单指令组成一段子程序来实现。比如RISC II共有39条指令，分为以下4类：
   1. 寄存器一寄存器操作：移位、逻辑、算数（整数）运算等12条。
   2. 取/存数指令，取存字节、半字、字等16条。
   3. 控制转移指令：条件转移、调用/返回等6条。
   4. 其他：存取程序状态字PSW和程序计数器等5条。
      一些常用指令未被选中，但用这些指令并在硬件系统的辅助下，足以实现其他一些指令的功能。例如：该机约定R₀寄存器的内容恒为0，这样加法指令可替代寄存器间的传递指令。即( R₁)+(R₀)→R₄替代了R₁→R₄
      加法指令还可以替代清楚寄存器指令，即(R₁)+(R₀)→R₄替代了0→R₄
      减法指令可替代取负数指令，即(R₀)−(R₁)→R₄替代了R₄寄存器内容取负
3. 比较 RISC 和 CISC 的异同之处。
   答：CISC体系结构的设计策略是使用大量的指令，包括复杂指令，每一项简单或复杂的任务都有一条对应的指令，程序员不需要写一大堆指令去完成一项复杂的任务。复杂的指令被转化为一系列简单操作然后由CPU执行。RISC体系结构的设计策略是使用少量的指令完成最少的简单操作，复杂指令用简单指令子集模拟，在RISC中进行程序设计比在其他设计中更难更费时，因为复杂指令都用简单指令来模拟。

第八章

1. 今有四级流水线，分别完成取指(IF)、译码并取数(ID)、执行(EX)、写结果(WR)4个步骤。假设完成各步操作的时间依次为 90ns、90ns、60 ns、45 ns。

   1. 流水线的时钟周期应取何值?
      流水线的时钟周期应按各步操作的最大时间来考虑，即流水线的时钟周期应取 90ns。
   2. 若相邻的指令发生数据相关,那么第2条指令安排推迟多少时间才能不发生错误?
      若相邻两条指令发生数据相关，需使第二条指令暂停执行，直到前面指令产生结果后，再执行第二条指令，因此至少要延迟两个时钟周期，即 180ns。
   3. 若相邻两指令发生数据相关,为了不推迟第2条指令的执行,可采取什么措施?
      若想不推迟第二条指令的执行，在硬件设计上可采取旁路技术，即设置直接传送数据的通路。其主要思想是不必待某条指令的执行结果送回到寄存器后，再从寄存器中取出该结果，作为下一条指令的源操作数，而是直接将执行结果送到其他指令所需要的地方。

2. 提高访存速度所采取的措施

3. 采用高速器件,选用存取周期短的芯片,可提高存储器的速度。

4. 采用缓存,CPU将最近期要用的信息先调入缓存,而缓存的速度比主存快得多,这样CPU每次只需从缓存中取出 (或存入)信息,从而缩短了访存时间,提高了访存速度。

5. 调整主存结构如采用单体多字结构(在一个存取周期内读出多个存储字可增加存储器的带宽)或采用多体结构存储器。

6. 在5个功能段的指令流水线中，假设每段的执行时间分别是10ns、8 ns、10ns、10ns和7ns。对于完成12条指令的流水线面言,其加速比为多少?该流水线的实际吞吐率为多少?
   加速比:流水线时钟周期至少为10ns.
   流水线完成12条指令所需时间$$(12-1)\times 10+5\times 10=160ns$$。
   非流水线完成12条指令所需时间$$12\times (10+8+10+10+7)=540ns$$。
   流水线加速比为540+160=3.375。
   实际吞吐率是指流水线完成n条指令的实际吞吐率。
   该流水线的实际吞叶率为$$12/[(12-1)\times \Delta t+5\times \Delta t]$$又因为$$\Delta t=10ns$$，所以实际吞吐率为: 0.075条/ns。

7. 什么是指令流水?画出指令二级流水和四级流水的示意图，它们中哪一个更能提高处理器速度,为什么?
   指令流水就是改变各条指令按顺序串行执行的规则，使机器在执行上一条指令的同时，取出下一条指令，下图（a）和（b）分别是指令的二级流水和四级流水示意图。
   

8. 什么是中断?设计中断系统需考虑哪些主要问题?
   CPU在程序运行过程中，遇到异常情况或特殊请求，需暂停现行程序，转至对这些异常情况或特殊请求的处理，处理完后再返回到原程序断点处继续执行，这一过程即为中断。设计中断系统需考虑如下几个问题。
   1. 中断源如何向CPU提出请求
   2. 当多个中断源同时提出请求时，CPU如何确定响应的优先次序
   3. CPU在什么情况(时间、条件)下响应中断
   4. 如何保护现场
   5. 如何寻找中断服务程序的入口地址
   6. 如何恢复现场
   7. 当出现中断嵌套时如何处理

9. 计算机为了管理中断,在硬件上通常有哪设置?各有何作用?对指令系统有何考虑？
   在计算机系统中，为了管理中断需设置下列这些硬件，以及它们的作用分别是：
   1. 中断请求触发器，其个数与中断源个数相等，用以标志某个中断源项 CPU 提出中断请求：
   2. 中断屏蔽触发器，其个数与中断请求触发器相等，当其为1时，表示该中断源的中断请求被屏蔽，CPU不能响应；
   3. 排队器，用来进行中断判优。当多个中断源同时请求时，排队器可选中优先级最高的中断请求；
   4. 向量地址形成部件，用以产生中断源的向量地址，从而可找到中断服务程序的入口地址
   5. 允许中断触发器，当其为1时，CPU 允许处理中断；
   6. 中断标志触发器，标志该系统进入中断周期；
   7. 堆栈，用来保护现场；
   8. 中断查询信息号电路。在每条指令执行周期结束时刻，该电路向各中断源发查询信号在计算机系统中，为了管理中断，指令系统应设有开中断、关中断、置屏蔽字及中断返回等指令。

10. 在中断系统中,INTR、INT、EINT这3个触发器各有何作用?
    INTR是中断请求触发器，每个中断源都对应一个 INTR，当其为“1”状态时，表示该中断源有请求。
    EINT 是允许中断触发器，当其为“1”时，表示 CPU 允许响应中断源的请求；当其为“0”时，意味着 CPU 禁止响应中断。
    INT是中断标记触发器，当其为“1”时，表示 CPU 进入中断周期。

第九章

1. 什么是指令周期、机器周期和时钟周期?三者有何关系?
   指令周期是CPU取出并执行一条指令所需的全部时间，即完成一条指令的时间。
   机器周期是所有指令执行过程中的一个基准时间，通常以存取周期作为机器周期。
   时钟周期是机器主频的倒数也可称为节拍，它是控制计算机操作的最小单位时间。
   一个指令周期包含若干个机器周期，一个机器周期又包含若干个时钟周期，每个指令周期内的机器周期数可以不等，每个机器周期内的时钟周期数也可以不等。
2. 能不能说CPU的主频越快,计算机的运行速度就越快?为什么?
   不能说机器的主频越快，机器的速度就越快。
   因为机器的速度不仅与主频有关，还与机器周期中所含的时钟周期以及指令周期中所含的机器周期数有关。同样主频的机器，由于机器周期所含的时钟周期数不同，机器的速度也不同。机器周期中所含时钟周期数少的机器，速度更快。
   此外，机器的速度还与其他很多因素有关，如主存的速度、机器是否配有 Cache、总线的数据传输率、硬盘的速度以及机器是否采用流水技术等等。机器速度还可以用 MIPS（每秒执行百万条指令数）和 CPI（执行一条指令所需的时钟周期数）来衡量。
3. 设机器A的CPU主频为8MHz,机器周期4个时钟周期,且该机的平均指令执行速度是0.4MIPS，试求该机的平均指令周期和机器周期,每个指令周期中含几个机器周期。如果机器B的CPU主频为12MHz，且机器周期也含4个时钟周期,试问B机的平均指令执行速度为多少 MIPS?
   由主频为8MHz，得时钟周期为$$1÷8=0.125\mu s$$，
   机器周期为$$0.125\times 4=0.5\mu s$$。
   根据平均指令执行速度为0.4MIPS，得平均指令周期为$$1÷0.4=2.5\mu s$$。
   每个指令含$$2.5÷0.5=5$$个机器周期。
   若主频为12MHz，得时钟周期为1/12μs，机器周期为$$4\times (1/12\mu s)=1/3\mu$$，指令执行周期为$$5\times 1/3\mu s$$。
   B机的平均指令执行速度为$$3/5=0.6MIPS$$。