【深度学习\数学建模】多元线性回归模型

训练线性回归模型的思路

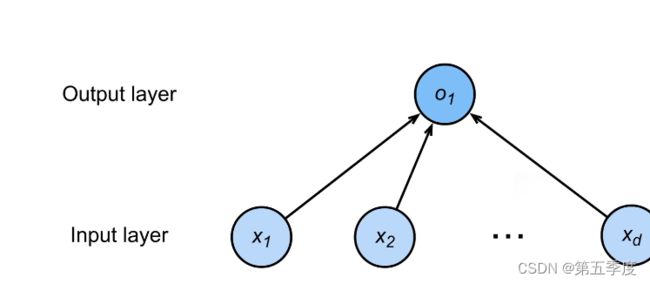
线性回归模型的一般形式为：
$$y=<\omega ,x>+b$$假如现在给定了1000个样本，分为特征（x1，x2，x3）和标签（y）：

从这些数据中训练出一个线性回归模型，就是确定两个参数 $\omega$ 和 $b$。步骤如下：

• 利用线性回归模型的计算式算出所有样本的预估值 $\hat{y}$。（线性模型的本质就是对所有样本的每一个特征进行线性组合再加上偏差）
• 计算预估值 $\hat{y}$ 与真实值 $y$（标签）之间的误差。误差使用损失函数表示：
  $$\iota \left(\omega ,b\right)=\frac{1}{2}{\left(<w,x>+b-y\right)}^2$$注意损失函数表示每一个样本在模型输出下对真实值的误差。 这个损失函数得到的结果是一个向量，我们的目标就是同时最小化这个向量中的每一个分量。“同时最小化向量中的每一个分量”与“将向量每一个分量求和，最小化这个和”是等价的。所以损失函数又表示为：
  $$\iota \left(\omega ,b\right)=sum\left(\frac{1}{2}{\left(<w,x>+b-y\right)}^2\right)$$这个损失函数接下来取哪个 $\omega$ 和 $b$ 能减小呢？这需要使用到梯度的概念。数学可以证明一个多元函数对每个自变量（某个点）求偏导并且将偏导组成向量，那么这个多元函数在这个点朝着向量的方向变化（增加/减少）最快。这个向量就叫做梯度。我们只需要把损失函数对 $\omega$ 和 $b$ 分别求梯度，就可以知道 $\omega$ 和 $b$ 接下来要往哪个方向走变化最快了。
• 根据求出的梯度对两个参数进行迭代。注意：这里梯度除以num_sample（样本个数），是因为上边求损失函数的时候进行了求和操作，之后求出的梯度方向不会变，但是大小扩大了num_sample倍，要恢复回原来的量纲。 $\eta$ 是学习率，既不能太大也不能太小。太大会导致损失函数值一直在最优解旁边振荡，使得损失函数无法收敛；太小会导致迭代次数过多（求解梯度的代价是非常大的，要尽量减少梯度的求解。）
  $$\begin{gathered} {\omega }_{i+1}={\omega }_i-\eta \frac{\nabla \iota \left(\omega \right)}{num\_sample} \\ {b}_{i+1}=b_i-\eta \frac{\nabla \iota \left(b\right)}{num\_sample} \end{gathered}$$
• 重复上边流程，就可以让两个参数不断学习，最后使损失函数收敛，把结果的两个参数代回公式，就得到线性回归模型了。

我们可以把线性回归视为一个简单的单层神经网络。

模型中的梯度下降、随机梯度下降和小批量梯度下降

上边知道了如何训练出一个线性回归模型，还有一些细节值得琢磨。
两个参数的迭代公式被称为梯度下降。
$$\begin{gathered} {\omega }_{i+1}={\omega }_i-\eta \frac{\nabla \iota \left(\omega \right)}{num\_sample} \\ {b}_{i+1}=b_i-\eta \frac{\nabla \iota \left(b\right)}{num\_sample} \end{gathered}$$这两个公式从减少计算时间的角度看，是可以继续优化的。$\nabla \iota \left(\omega \right)$和$\nabla \iota \left(b\right)$都是标签求和之后对参数的梯度，“求和”这一操作，在样本数量多达数十万乃至上百万的时候，是非常耗性能的。
上边这种求法，被成为批量梯度下降（Batch gradient descent, BGD）。优点是利用了样本和标签的所有信息，最后训练出来的模型是最准确的。缺点就是太慢了。
针对太慢这个问题，有一种解决方法：随机梯度下降（Stochastic gradient Descent, SGD）。这种方法每次都只取一个样本去求损失函数、进行梯度下降更新参数，速度上无疑快了很多。但是也有缺点：每次只取一个样本，信息量大幅度减少，训练出来的模型不够准确。
针对上面两种方法的缺点，又有一种方法：小批量梯度下降（Mini-batch gradient Descent, MBGD）。这种方法每次取batch_size个样本去求损失函数、进行梯度下降更新参数，对求解时间和求解质量进行了权衡处理。所以，我们采用小批量梯度下降进行参数的迭代。

线性回归模型实现

使用pytorch从零实现

import random

import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


def synthetic_data(w, b, num_samples):
    """
    生成带噪的线性回归feature和label
    :param w: 线性回归的权重
    :param b: 线性回归的偏差
    :param num_samples: 要生成的样本数量
    :return: 生成的特征和标签
    """
    x = torch.normal(0, 1, (num_samples, len(w)))
    y = torch.matmul(x, w) + b
    y = y + torch.normal(0, 1, y.shape)
    # 现在y是行向量，为了跟x样本对齐，把它变成列向量
    y = y.reshape(-1, 1)
    return x, y


def data_iter(batch_size, features, labels):
    """
    随机选取batch_size数量的特征和标签
    :param batch_size: 批量大小
    :param features: 特征
    :param labels: 标签
    :return: 返回随机选取batch_size数量的特征和标签
    """
    indices = list(range(len(labels)))
    random.shuffle(indices)
    for i in range(0, len(labels), batch_size):
        indices_tensor = torch.tensor(indices[i:min(i + batch_size, len(labels))])
        yield features[indices_tensor], labels[indices_tensor]


def linreg(w, b, x):
    """
    线性回归模型
    :param w: 权重，需要是列向量，不然线性组合会失败
    :param b: 偏差
    :param x: 特征
    :return: 返回线性回归模型
    """
    return  torch.mm(x, w) + b


def square_loss(y_hat, y):
    """
    损失函数是均方误差
    """
    return ((y_hat - y) ** 2) / 2


def mbgd(lr, batch_size, w, b):
    """
    小批量梯度下降
    :param lr: 
    :param batch_size: 
    :param w: 
    :param b: 
    :return: 
    """
    # 这里写torch.no_grad()是为了优化性能
    with torch.no_grad():
        w -= lr * (w.grad / batch_size)
        b -= lr * (b.grad / batch_size)
        w.grad.zero_()
        b.grad.zero_()


features, labels = synthetic_data(torch.tensor([2.0, -3.0]), 4.2, 1000)
# 模型的参数
batch_size = 10
lr = 0.01
# 学习次数
num_epoch = 6
w = torch.normal(0, 0.01, (features.size(1), 1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)

for i in range(num_epoch):
    for batch_features, batch_labels in data_iter(batch_size=batch_size, features=features, labels=labels):
        # 模型求解得到预估值
        y_hat = linreg(w, b, batch_features)
        # 损失函数
        loss = square_loss(y_hat, batch_labels)
        # 求梯度
        loss.sum().backward()
        # 迭代优化
        mbgd(lr=lr, batch_size=batch_size, w=w, b=b)
    # torch.no_grad()表示这一块不需要用到求梯度的操作，可以优化性能
    with torch.no_grad():
        print("*" * 50)
        print("loss:{}".format(square_loss(linreg(w,b,features),labels).sum()))
        print("w,b:{},{}".format(w,b))
        print("*" * 50)

# 画图
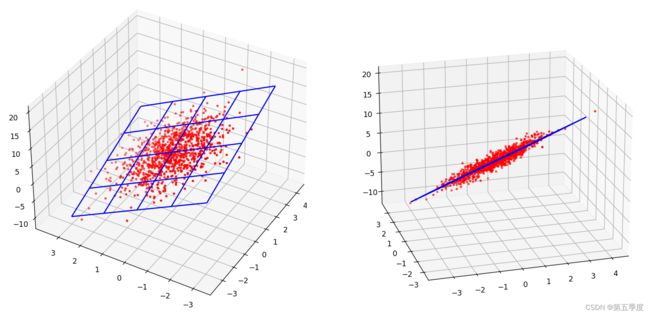
fig=plt.figure()
ax = fig.add_subplot(111,projection="3d")
x = np.linspace(-3,3,5)
y = np.linspace(-3,3,5)
x,y = np.meshgrid(x,y)
z = x * w[0].detach().numpy() +y * w[1].detach().numpy()+b.detach().numpy()
ax.scatter3D(features[:,0].detach().numpy(),features[:,1].detach().numpy(),labels.detach().numpy(),color="red",s=5)
ax.plot_wireframe(x,y,z,color='blue')
plt.show()

直接调用pytorch的库实现

import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn
from torch.utils import data


def synthetic_data(w, b, num_samples):
    """
    生成带噪的线性回归feature和label
    :param w: 线性回归的权重
    :param b: 线性回归的偏差
    :param num_samples: 要生成的样本数量
    :return: 生成的特征和标签
    """
    x = torch.normal(0, 1, (num_samples, len(w)))
    y = torch.matmul(x, w) + b
    y = y + torch.normal(0, 1, y.shape)
    # 现在y是行向量，为了跟x样本对齐，把它变成列向量
    y = y.reshape(-1, 1)
    return x, y

def load_array(data_arrays,batch_size,is_shuffle):
    """构造一个pytorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset=dataset,batch_size=batch_size,shuffle=is_shuffle)

true_w = torch.tensor([2.0,-3.4])
true_b = 4.2
features,labels = synthetic_data(true_w,true_b,1000)
# 获得数据迭代器
data_iter = load_array((features,labels),10,True)
# 构建单层的线性神经网络（全连接层），具有2个特征输入，1个输出
net = nn.Sequential(nn.Linear(2,1))
# 第一层就是网络的索引0。初始化第一层网络的w和b
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
# 误差函数
loss = nn.MSELoss()
# 梯度下降优化器
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

# 开始训练
num_epoch = 6
for i in range(num_epoch):
    for batch_features,batch_labels in data_iter:
        # 计算损失
        l = loss(net(batch_features),batch_labels)
        # 手动把梯度清空
        trainer.zero_grad()
        # 求梯度(这里默认封装了sum())
        l.backward()
        # 梯度下降
        trainer.step()
    print("="*25)
    l = loss(net(features),labels)
    print(f"epoch{i},loss:{l:f}")
    print(net[0].weight.data)
    print(net[0].bias.data)
    print("="*25)
# 画图
fig=plt.figure()
ax = fig.add_subplot(111,projection="3d")
x = np.linspace(-3,3,5)
y = np.linspace(-3,3,5)
x,y = np.meshgrid(x,y)
z = x * net[0].weight[:,0].detach().numpy() +y * net[0].weight[:,1].detach().numpy()+net[0].bias.detach().numpy()
ax.scatter3D(features[:,0].detach().numpy(),features[:,1].detach().numpy(),labels.detach().numpy(),color="red",s=5)
ax.plot_wireframe(x,y,z,color='blue')
plt.show()