从实现角度介绍如何线性时间建立后缀树
The following is an attempt to describe the Ukkonen algorithm by first showing what it does when the string is simple (i.e. does not contain any repeated characters), and then extending it to the full algorithm.
First, a few preliminary statements.
- What we are building, is basically like a search trie. So there is a root node, edges going out of it leading to new nodes, and further edges going out of those, and so forth
- But: Unlike in a search trie, the edge labels are not single characters. Instead, each edge is labeled using a pair of integers [from,to]. These are pointers into the text. In this sense, each edge carries a string label of arbitrary length, but takes only O(1) space (two pointers).
Basic principle
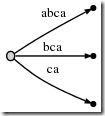
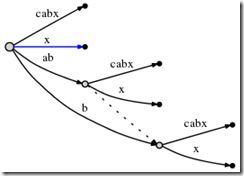
I would like to first demonstrate how to create the suffix tree of a particularly simple string, a string with no repeated characters:
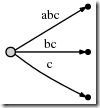
abc
The algorithm works in steps, from left to right. There is one step for every character of the string. Each step might involve more than one individual operation, but we will see (see the final observations at the end) that the total number of operations is O(n).
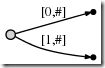
So, we start from the left, and first insert only the single character a by creating an edge from the root node (on the left) to a leaf, and labeling it as [0,#], which means the edge represents the substring starting at position 0 and ending at the current end. I use the symbol # to mean the current end, which is at position 1 (right after a).
So we have an initial tree, which looks like this:
And what it means is this:
Now we progress to position 2 (right after b). Our goal at each step is to insert all suffixes up to the current position. We do this by
- expanding the existing a-edge to ab
- inserting one new edge for b
In our representation this looks like
And what it means is:
We observe two things:
- The edge representation for ab is the same as it used to be in the initial tree: [0,#]. Its meaning has automatically changed because we updated the current position # from 1 to 2.
- Each edge consumes O(1) space, because it consists of only two pointers into the text, regardless of how many characters it represents.
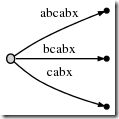
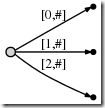
Next we increment the position again and update the tree by appending a c to every existing edge and inserting one new edge for the new suffix c.
In our representation this looks like
And what it means is:
We observe:
- The tree is the correct suffix tree up to the current position after each step
- There are as many steps as there are characters in the text
- The amount of work in each step is O(1), because all existing edges are updated automatically by incrementing #, and inserting the one new edge for the final character can be done in O(1) time. Hence for a string of length n, only O(n) time is required.
First extension: Simple repetitions
Of course this works so nicely only because our string does not contain any repetitions. We now look at a more realistic string:
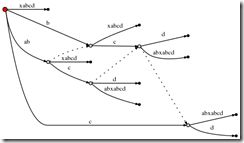
abcabxabcd
It starts with abc as in the previous example, then ab is repeated and followed by x, and then abcis repeated followed by d.
Steps 1 through 3: After the first 3 steps we have the tree from the previous example:
Step 4: We move # to position 4. This implicitly updates all existing edges to this:
and we need to insert the final suffix of the current step, a, at the root.
Before we do this, we introduce two more variables (in addition to #), which of course have been there all the time but we haven't used them so far:
- The active point, which is a triple (active_node,active_edge,active_length)
- The remainder, which is an integer indicating how many new suffixes we need to insert
The exact meaning of these two will become clear soon, but for now let's just say:
- In the simple abc example, the active point was always (root,'\0x',0), i.e. active_node was the root node, active_edge was specified as the null character '\0x', and active_length was zero. The effect of this was that the one new edge that we inserted in every step was inserted at the root node as a freshly created edge. We will see soon why a triple is necessary to represent this information.
- The remainder was always set to 1 at the beginning of each step. The meaning of this was that the number of suffixes we had to actively insert at the end of each step was 1 (always just the final character).
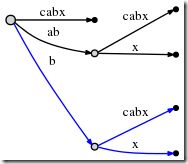
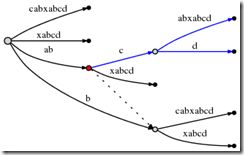
Now this is going to change. When we insert the current final character a at the root, we notice that there is already an outgoing edge starting with a, specifically: abca. Here is what we do in such a case:
- We do not insert a fresh edge [4,#] at the root node. Instead we simply notice that the suffix a is already in our tree. It ends in the middle of a longer edge, but we are not bothered by that. We just leave things the way they are.
- We set the active point to (root,'a',1). That means the active point is now somewhere in the middle of outgoing edge of the root node that starts with a, specifically, after position 1 on that edge. We notice that the edge is specified simply by its first character a. That suffices because there can be only one edge starting with any particular character (confirm that this is true after reading through the entire description).
- We also increment remainder, so at the beginning of the next step it will be 2.
Observation: When the final suffix we need to insert is found to exist in the tree already, the tree itself is not changed at all (we only update the active point and remainder). The tree is then not an accurate representation of the suffix tree up to the current position any more, but it contains all suffixes (because the final suffix a is contained implicitly). Hence, apart from updating the variables (which are all of fixed length, so this is O(1)), there was no work done in this step.
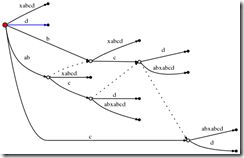
Step 5: We update the current position # to 5. This automatically updates the tree to this:
And because remainder is 2, we need to insert two final suffixes of the current position: ab and b. This is basically because:
- The a suffix from the previous step has never been properly inserted. So it has remained, and since we have progressed one step, it has now grown from a to ab.
- And we need to insert the new final edge b.
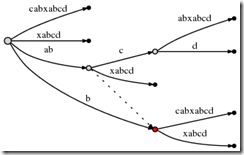
In practice this means that we go to the active point (which points to behind the a on what is now theabcab edge), and insert the current final character b. But: Again, it turns out that b is also already present on that same edge.
So, again, we do not change the tree. We simply:
- Update the active point to (root,'a',2) (same node and edge as before, but now we point to behind the b)
- Increment the remainder to 3 because we still have not properly inserted the final edge from the previous step, and we don't insert the current final edge either.
To be clear: We had to insert ab and b in the current step, but because ab was already found, we updated the active point and did not even attempt to insert b. Why? Because if ab is in the tree,every suffix of it (including b) must be in the tree, too. Perhaps only implicitly, but it must be there, because of the way we have built the tree so far.
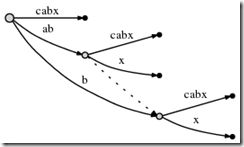
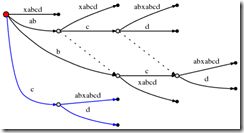
We proceed to step 6 by incrementing #. The tree is automatically updated to:
Because remainder is 3, we have to insert abx, bx and x. The active point tells us where abends, so we only need to jump there and insert the x. Indeed, x is not there yet, so we split theabcabx edge and insert an internal node:
The edge representations are still pointers into the text, so splitting and inserting an internal node can be done in O(1) time.
So we have dealt with abx and decrement remainder to 2. Now we need to insert the next remaining suffix, bx. But before we do that we need to update the active point. The rule for this, after splitting and inserting an edge, will be called Rule 1 below, and it applies whenever the active_node is root (we will learn rule 3 for other cases further below). Here is rule 1:
After an insertion from root,
- active_node remains root
- active_edge is set to the first character of the new suffix we need to insert, i.e. b
- active_length is reduced by 1
Hence, the new active-point triple (root,'b',1) indicates that the next insert has to be made at thebcabx edge, behind 1 character, i.e. behind b. We can identify the insertion point in O(1) time and check whether x is already present or not. If it was present, we would end the current step and leave everything the way it is. But x is not present, so we insert it by splitting the edge:
Again, this took O(1) time and we update remainder to 1 and the active point to (root,'x',0) as rule 1 states.
But there is one more thing we need to do. We'll call this Rule 2:
If we split an edge and insert a new node, and if that is not the first node created during the current step, we connect the previously inserted node and the new node through a special pointer, a suffix link. We will later see why that is useful. Here is what we get, the suffix link is represented as a dotted edge:
We still need to insert the final suffix of the current step, x. Since the active_length component of the active node has fallen to 0, the final insert is made at the root directly. Since there is no outgoing edge at the root node starting with x, we insert a new edge:
As we can see, in the current step all remaining inserts were made.
We proceed to step 7 by setting #=7, which automatically appends the next character, a, to all leaf edges, as always. Then we attempt to insert the new final character to the active point (the root), and find that it is there already. So we end the current step without inserting anything and update the active point to (root,'a',1).
In step 8,, #=8, we append b, and as seen before, this only means we update the active point to(root,'a',2) and increment remainder without doing anything else, because b is already present. However, we notice (in O(1) time) that the active point is now at the end of an edge. We reflect this by re-setting it to (node1,'\0x',0). Here, I use node1 to refer to the internal node the abedge ends at.
Then, in step #=9, we need to insert 'c' and this will help us to understand the final trick:
Second extension: Using suffix links
As always, the # update appends c automatically to the leaf edges and we go to the active point to see if we can insert 'c'. It turns out 'c' exists already at that edge, so we set the active point to(node1,'c',1), increment remainder and do nothing else.
Now in step #=10, remainder is 4, and so we first need to insert abcd (which remains from 3 steps ago) by inserting d at the active point.
Attempting to insert d at the active point causes an edge split in O(1) time:
The active_node, from which the split was initiated, is marked in red above. Here is the final rule,Rule 3:
After splitting an edge from an active_node that is not the root node, we follow the suffix link going out of that node, if there is any, and reset the active_node to the node it points to. If there is no suffix link, we set the active_node to the root. active_edge and active_length remain unchanged.
So the active point is now (node2,'c',1), and node2 is marked in red below:
Since the insertion of abcd is complete, we decrement remainder to 3 and consider the next remaining suffix of the current step, bcd. Rule 3 has set the active point to just the right node and edge so inserting bcd can be done by simply inserting its final character d at the active point.
Doing this causes another edge split, and because of rule 2, we must create a suffix link from the previously inserted node to the new one:
We observe: Suffix links enable us to reset the active point so we can make the next remaining insert at O(1) effort. Look at the graph above to confirm that indeed node at label ab is linked to the node at b(its suffix), and the node at abc is linked to bc.
The current step is not finished yet. remainder is now 2, and we need to follow rule 3 to reset the active point again. Since the current active_node (red above) has no suffix link, we reset to root. The active point is now (root,'c',1).
Hence the next insert occurs at the one outgoing edge of the root node whose label starts with c:cabxabcd, behind the first character, i.e. behind c. This causes another split:
And since this involves the creation of a new internal node,we follow rule 2 and set a new suffix link from the previously created internal node:
(I am using Graphviz Dot for these little graphs. The new suffix link caused dot to re-arrange the existing edges, so check carefully to confirm that the only thing that was inserted above is a new suffix link.)
With this, remainder can be set to 1 and since the active_node is root, we use rule 1 to update the active point to (root,'d',0). This means the final insert of the current step is to insert a single d at root:
That was the final step and we are done. There are number of final observations, though:
- In each step we move # forward by 1 position. This automatically updates all leaf nodes in O(1) time.
- But it does not deal with a) any suffixes remaining from previous steps, and b) with the one final character of the current step.
- remainder tells us how many additional inserts we need to make. These inserts correspond one-to-one to the final suffixes of the string that ends at the current position #. We consider one after the other and make the insert. Important: Each insert is done in O(1) time since the active point tells us exactly where to go, and we need to add only one single character at the active point. Why? Because the other characters are contained implicitly (otherwise the active point would not be where it is).
- After each such insert, we decrement remainder and follow the suffix link if there is any. If not we go to root (rule 3). If we are at root already, we modify the active point using rule 1. In any case, it takes only O(1) time.
- If, during one of these inserts, we find that the character we want to insert is already there, we don't do anything and end the current step, even if remainder>0. The reason is that any inserts that remain will be suffixes of the one we just tried to make. Hence they are all implicit in the current tree. The fact that remainder>0 makes sure we deal with the remaining suffixes later.
- What if at the end of the algorithm remainder>0? This will be the case whenever the end of the text is a substring that occurred somewhere before. In that case we must append one extra character at the end of the string that has not occurred before. In the literature, usually the dollar sign $ is used as a symbol for that. Why does that matter? --> If later we use the completed suffix tree to search for suffixes, we must accept matches only if they end at a leaf. Otherwise we would get a lot of spurious matches, because there are many strings implicitly contained in the tree that are not actual suffixes of the main string. Forcing remainder to be 0 at the end is essentially a way to ensure that all suffixes end at a leaf node. However, if we want to use the tree to search for general substrings, not only suffixes of the main string, this final step is indeed not required, as suggested by the OP's comment below.
- So what is the complexity of the entire algorithm? If the text is n characters in length, there are obviously n steps (or n+1 if we add the dollar sign). In each step we either do nothing (other than updating the variables), or we make remainder inserts, each taking O(1) time. Since remainderindicates how many times we have done nothing in previous steps, and is decremented for every insert that we make now, the total number of times we do something is exactly n (or n+1). Hence, the total complexity is O(n).
- However, there is one small thing that I did not properly explain: It can happen that we follow a suffix link, update the active point, and then find that its active_length component does not work well with the new active_node. For example, consider a situation like this:
(The dashed lines indicate the rest of the tree. The dotted line is a suffix link.)
Now let the active point be (red,'d',3), so it points to the place behind the f on the defg edge. Now assume we made the necessary updates and now follow the suffix link to update the active point according to rule 3. The new active point is (green,'d',3). However, the d-edge going out of the green node is de, so it has only 2 characters. In order to find the correct active point, we obviously need to follow that edge to the blue node and reset to (blue,'f',1).
In a particularly bad case, the active_length could be as large as remainder, which can be as large as n. And it might very well happen that to find the correct active point, we need not only jump over one internal node, but perhaps many, up to n in the worst case. Does that mean the algorithm has a hidden O(n2) complexity, because in each step remainder is generally O(n), and the post-adjustments to the active node after following a suffix link could be O(n), too?
No. The reason is that if indeed we have to adjust the active point (e.g. from green to blue as above), that brings us to a new node that has its own suffix link, and active_length will be reduced. As we follow down the chain of suffix links we make the remaining inserts, active_length can only decrease, and the number of active-point adjustments we can make on the way can't be larger thanactive_length at any given time. Since active_length can never be larger than remainder, and remainder is O(n) not only in every single step, but the total sum of increments ever made toremainder over the course of the entire process is O(n) too, the number of active point adjustments is also bounded by O(n).
转自: http://stackoverflow.com/questions/9452701/ukkonens-suffix-tree-algorithm-in-plain-english

![clip_image005[1] clip_image005[1]](http://img.e-com-net.com/image/product/1e488542485b46f392588bbf546c7b7e.jpg)