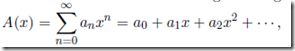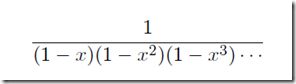整数划分 Integer Partition(一)
话说今天百度面试,可能是由于我表现的不太好,面试官显得有点不耐烦,说话的语气也很具有嘲讽的意思,搞得我有点不爽。Whatever,面试中有问到整数划分问题,回答这个问题过程中被面试官搞的不胜其烦,最后也给出了其动态规划的算法,但是显然,醉翁之意不在动态规划而在于生成函数(generating function)。下面开始吧:
参考:http://www.skymoon.biz/?p=192 (问题定义以及动态规划)
http://www.artofproblemsolving.com/Resources/Papers/LaurendiPartitions.pdf (生成函数)
http://www.cnblogs.com/hoodlum1980/archive/2008/10/11/1308493.html(部分代码实现)
本系列有两篇文章,会分为下面三个部分,首先我会简单介绍一下动态规划的解法,然后会介绍生成函数的解法,第三部分(在下一篇文章中说明)做一下生成函数的扩展。要求读者具备基本的动态规划常识以及生成函数概念。
文章最后有我最喜欢的东西。
先说明一下问题,什么是整数划分?
- n=m1+m2+...+mi; (其中mi为正整数,并且1 <= mi <= n),则{m1,m2,...,mi}为n的一个划分。
- 如果{m1,m2,...,mi}中的最大值不超过m,即max(m1,m2,...,mi)<=m,则称它属于n的一个m划分。这里我们记n的m划分的个数为f(n,m);
- 举个例子,当n=5时我们可以获得以下这几种划分(注意,例子中m>=5)
5 = 5
= 4 + 1
= 3 + 2
= 3 + 1 + 1
= 2 + 2 + 1
= 2 + 1 + 1 + 1
= 1 + 1 + 1 + 1 + 1
一、 动态规划解法
根据n和m的关系,考虑以下几种情况:
1. 当n=1时,不论m的值为多少(m>0),只有一种划分即{1};
2. 当m=1时,不论n的值为多少,只有一种划分即n个1,{1,1,1,...,1};
3. 当n=m时,根据划分中是否包含n,可以分为两种情况:
(1) 划分中包含n的情况,只有一个即{n};
(2) 划分中不包含n的情况,这时划分中最大的数字也一定比n小,即n的所有(n-1)划分。因此 f(n,n) =1 + f(n,n-1);
4. 当n<m时,由于划分中不可能出现负数,因此就相当于f(n,n);
5. 但n>m时,根据划分中是否包含最大值m,可以分为两种情况:
(1) 划分中包含m的情况,即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m,可能再次出现m,因此是(n-m)的m划分,因此这种划分个数为f(n-m, m);
(2) 划分中不包含m的情况,则划分中所有值都比m小,即n的(m-1)划分,个数为f(n,m-1);因此 f(n, m) = f(n-m, m)+f(n,m-1);
综合以上情况,我们可以看出,上面的结论具有递归定义特征,其中(1)和(2)属于回归条件,(3)和(4)属于特殊情况,将会转换为情况(5)。而情况(5)为通用情况,属于递推的方法,其本质主要是通过减小m以达到回归条件,从而解决问题。其递推表达式如下:
- f(n, m)= 1; (n=1 or m=1)
- f(n, m)=f(n, n); (n<m)
- 1+ f(n, m-1); (n=m)
- f(n-m,m)+f(n,m-1); (n>m)
据此我们获得了动态规划的代码:
1: #include<iostream>
2:
3: using namespacestd;
4:
5: int equationCount(intn,intm)
6: {
7: if(n==1||m==1)
8: return 1;
9: else if(n<m)
10: return equationCount(n,n);
11: else if(n==m)
12: return 1+equationCount(n,n-1);
13: else
14: return equationCount(n,m-1)+equationCount(n-m,m);
15: }
16:
17: int main(void)
18: {
19: in tn;
20: while(scanf("%d",&n)!=EOF&&(n>=1&&n<=120))
21: {
22: printf("%d\n",equationCount(n,n));
23: }
24: return 0;
25: }
几个变种:
(一)要求1,2,3,4..,m中每个数只允许使用一次的时?
此时我们需要调整我们的状态转换公式。
f(n-m,m)+f(n,m-1); (n>m) 应该更改为:f(n-m,m-1)+f(n,m-1); (n>m)
为什呢?因为每个数最多使用一次,f(n-m,m-1)表示我们取了数m,f(n,m-1)表示我们没取,但是无论取不取数m我们以后都不会再次取数m了。
当然喽,我们还需要调整边界状态:当m=1时,f(n,m)=1;当n=1而m>1时,f(n,m)=0。
其他不变!
(二)要求只能取1,2,3,4,..,m中的奇数?(默认m为奇数,如果不是则m=m-1)
这个呢,我们首先需要调整边界状态:当m=1时,f(n,m)=1;当n=1而m>1时,f(n,m)=0
其次,我们需要调整状态转换公式:
f(n-m,m)+f(n,m-1); (n>m) 应该更改为:f(n-m,m)+f(n,m-2); (n>m)
这是因为我们不能取偶数,故而当m为奇数的时候,m-1为偶数(只能被选择0次),f(n,m-1)=f(n,m-2);
(三)要求我们所取的 (n=m1+m2+...+mi )中 m1 m2 ... mi连续,比如5=1+4就不符合要求了。
这个的话,需要做一下转换,留待下一篇文章说明
注意,一般而言动态规划算法是用非递归从下往上计算的,上述代码采用递归形式只是为了便于理解,真正实现的话最好采用非递归形式。
二、 生成函数解法
先简单说明一下生成函数吧,下面是一个生成函数,
xk的系数ak代表了可获得数字k的组合数。
那么回到我们的问题中,我们怎么用生成函数去解决呢?
类似的,我们可以计算生成函数:
计算出来的xk的系数ak就是我们需要的划分数了。我们来详细说明一下为什么是这样。考虑一下x3,我们可以在第一个括号里面选择x、在第二个括号里面选择x2、其他括号选择1,这种方式来得到;同样的,我们也可以通过在第三个括号里面选择x3,其他扩号里面选择1,这种方式来获得。那么这跟生成函数有什么关系呢?
我们来做一个说明,第i个括号(1+xi+x2i+x3i · · ·)选择的元素代表了数字i在我们最终的划分中出现的次数,具体而言,如果我们在第i个括号中选择了元素 xc(i) * i 则表示数字 i 在我们最终的划分中出现了c(i)次。如果我们把最终从每个括号里面选择出来的元素相乘 x1 * c(1) · x2 * c(2) · x3 * c(3) · · · = x c(1) + 2 * c(2) + 3 * c(3)···.那么,xn的系数就是我们可以获得多少种不同的方式使得c(1) + 2 * c(2) + 3 * c(3)··· = n,也就是n的划分数(其中,c(i)代表了在一次划分中数字 i 的出现次数)。比如说25=6+4+4+3+2+2+2+1+1,用上式表示就是25=1(2)+2(3)+3(1)+4(2)+5(0)+6(1),也就是在划分中有两个1,三个2,一个3,两个4,0个5以及一个6。
假设x<1,那么我们可以将上面的生成函数表示为:
这将给我们第三部分的扩展带来方便。
考虑到我们能选择的最大的数 i 是 m ,所以真正计算的时候我们需要对上面的生成函数式子做一下修改:
G(x) = (1+x+x^2+x^3+...+x^n) (1+x^2+x^4+...) (1+x^3+x^6+...) ... (1+x^m)
= g(x,1) g(x,2) g(x,3) ... g(x, n)
代码实现如下:
1: #define N 130
2: unsigned long a[N];/*多项式a的系数数组*/
3: unsigned long b[N];/*多项式b的系数数组*/
4: unsigned long c[N];/*存储多项式a*b的结果*/
5:
6: /*两个多项式进行乘法,系数分别在a和b中,结果保存到c ,项最大次数到N */
7: /*注意这里我们只需要计算到前N项就够了。*/
8: void Poly()
9: {
10: int i,j;
11: memset(c,0,sizeof(c));
12: for(i=0; i<N; i++)
13: for(j=0; j<N-i; j++) /*y<N-i: 确保i+j不会越界*/
14: c[i+j] += a[i]*b[j];
15: }
16:
17: /*计算出前N项系数!即g(x,1) g(x,2)... g(x,n)的展开结果*/
18: void Init()
19: {
20: int i,k;
21: memset(a,0,sizeof(a));
22: memset(c,0,sizeof(c));
23: for(i=0;i<N;i++) a[i]=1; /*第一个多项式:g(x, 1) = x^0 + x^1 + x^2 + x^3 + */
24: for(k=2;k<N;k++)
25: {
26: memset(b,0,sizeof(b));
27: for(i=0;i<N;i+=k) b[i]=1;/*第k个多项式:g(x, k) = x^0 + x^(k) + x^(2k) + x^(3k) + */
28: Poly(); /* 多项式乘法:c= a*b */
29: memcpy(a,c,sizeof(c)); /*把相乘的结果从c复制到a中:c=a; */
30: }
31: }
好了,我们来看几个变种:
(一)要求1,2,3,4..,m中每个数只允许使用一次的时?
这个简单,将生成函数式子改为
G(x) = (1+x) (1+x^2) (1+x^3) ... (1+x^m) = g(x,1) g(x,2) g(x,3) ... g(x, n)就可以了
(二)要求只能取1,2,3,4,..,m中的奇数?(默认m为奇数,如果不是则m=m-1)
这个也简单,调整生成函数的式子为:
G(x) = (1+x+x^2+x^3+...+x^n)(1+x^3+x^6+...) ... (1+x^m)
= g(x,1) g(x,2) g(x,3) ... g(x, n)
(三)要求我们所取的 (n=m1+m2+...+mi )中 m1 m2 ... mi连续,比如5=1+4就不符合要求了。
这个呢,我们需要做一点转换
最后我们来证明一下变种一和变种二是一样的: