代码随想录算法训练营Day14 | 二叉树理论 | 递归遍历 | 迭代遍历 | 统一迭代
文章目录
- 二叉树理论
-
- 二叉树种类
-
- Complete binary tree
- Complete binary tree
- Binary search tree
- Balanced binary search tree(AVL)
- 储存方式
- 遍历二叉树
-
- BFS 的遍历顺序
- 二叉树定义
- 递归遍历
-
- 前序遍历 - 递归 (144)
- 后序遍历 - 递归 (145)
- 中序遍历 - 递归 (94)
- 迭代遍历
-
- 前序遍历 - 迭代
- 后序遍历 - 迭代
- 中序遍历 - 迭代
- 统一迭代
-
- 前序遍历 - 统一
- 后序遍历 - 统一
- 中序遍历 - 统一
二叉树理论
理论基础
二叉树种类
Complete binary tree
定义:每个 node 的 degree 为 0 或 2,且 degree=0 的 nodes 都在同一层。
depth=k 的树共有 2 k − 1 2^k-1 2k−1 个 nodes。
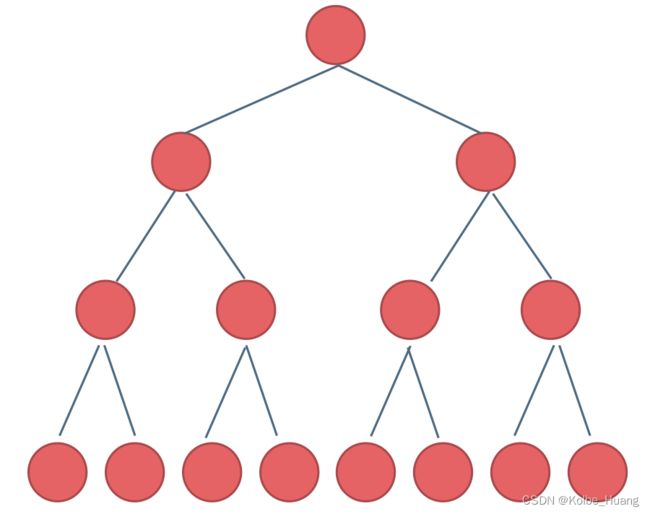
Complete binary tree
定义:
- 除了最后一层,每一层都是填满的
- 最后一层的 nodes 都尽可能向左填充

Binary search tree
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 它的左、右子树也分别为 binary search tree
Balanced binary search tree(AVL)
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
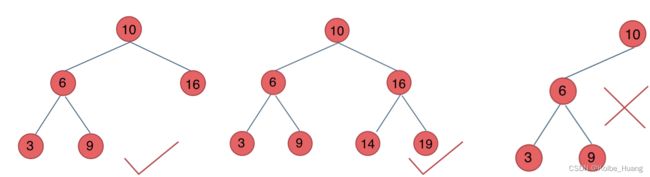
储存方式
- 链式储存:依靠指针连接 node 和 subnodes,类似链表。
- 顺序储存:使用数组进行储存(从0开始 index)。
- 如果节点的 index 为 i,左节点的 index 为 2*i + 1,右节点的 index 为 2*i + 2
遍历二叉树
- 深度优先搜索(DFS):搜索单个节点,直到碰到 leaf node 再往回走。
- 通常使用递归来实现,但也可以使用迭代(非递归)进行。
- 前序遍历
- 中序遍历
- 后序遍历
- 深度优先通常使用递归实现,即栈的结构
- 广度优先搜索(BFS):完成当前层的搜索,再进入下一层(一层一层)
- 层次遍历(迭代)
- 使用队列,FIFO 的规则符合一层一层的需求
BFS 的遍历顺序
前/中/后序遍历,其实指的就是中间节点的遍历顺序(中间节点出现在哪里)。
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中

二叉树定义
class TreeNode:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right
递归遍历
理论基础
递归的核心:
- 确定递归函数的参数、返回值
- 确定哪些参数是递归的过程中需要处理的
- 明确每次递归的返回值是什么
- 确定递归的终止条件
- 递归发生栈溢出的报错时,代表了递归的结束条件错误(或者压根没写)。由于递归是通过栈来实现的,没有正确终止的话,内存栈必然会溢出。
- 确定单层递归的逻辑
- 理解在每一层递归中要做什么,哪些部分是要 explicitly 处理的,哪些是要交给递归处理。
前序遍历 - 递归 (144)
题目链接
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
left_lst = self.preorderTraversal(root.left)
right_lst = self.preorderTraversal(root.right)
return [root.val] + left_lst + right_lst
后序遍历 - 递归 (145)
题目链接
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
left_lst = self.postorderTraversal(root.left)
right_lst = self.postorderTraversal(root.right)
return left_lst + right_lst + [root.val]
中序遍历 - 递归 (94)
题目链接
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
left_lst = self.inorderTraversal(root.left)
right_lst = self.inorderTraversal(root.right)
return left_lst + [root.val] + right_lst
迭代遍历
理论基础
一般面试中不会要求用迭代的方法实现复杂的题目,主要是考察以非递归的方式实现简单题目的能力。
递归的底层使用栈来实现的,所以迭代的时候其实也是要用栈来实现(相当于手动实现递归)。
但要注意,栈的 LIFO 的特性导致加入元素的顺序应当与最终数组里的结果是相反的。
前序遍历 - 迭代
通过栈的特性,来完成实质上的递归:每当栈的 top element 发生改变的时候,实质是开始了子树的递归。
因为栈的 LIFO,操作时的入栈顺序是中右左。
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = [root]
results = []
while (len(stack) > 0):
curr_node = stack.pop()
results.append(curr_node.val) # middle
if curr_node.right != None: # right
stack.append(curr_node.right)
if curr_node.left != None: # left
stack.append(curr_node.left)
return results
后序遍历 - 迭代
与前序遍历是一样的,只需要进行一些顺序的翻转即可(前序是“中左右”,后序是“左右中”)。
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = [root]
results = []
while (len(stack) > 0):
curr_node = stack.pop()
results.append(curr_node.val)
if curr_node.left != None:
stack.append(curr_node.left)
if curr_node.right != None:
stack.append(curr_node.right)
results.reverse()
return results
中序遍历 - 迭代
中序遍历和前后序遍历的代码基础是不同的,没办法像后序一样直接在前序的基础上修改。区别在于,中序遍历的访问节点和处理节点是不同的。
- 访问节点:遍历二叉树的节点
- 处理节点:将当前节点的值放入数组中
当访问根节点的时候,想要先处理左子树中的元素(而非像之前一样,先处理根节点),所以只有访问到最左边的 leaf 节点时,才能开始处理节点。解决思路是用栈进行其中的记录,而用指针来访问节点,而不像之前一样访问即可以处理。
主要逻辑:
- 从根节点开始,一路访问左子节点,直到 None
- 当遇到 None 的时候,pop 栈中的 top element(也就是此时的节点的根节点),同时检查该根节点(pop出去的元素)的右子节点
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = []
results = []
curr_node = root
while (len(stack) > 0 or curr_node != None):
if curr_node != None:
stack.append(curr_node)
curr_node = curr_node.left # left
else:
curr_node = stack.pop()
results.append(curr_node.val) # middle
curr_node = curr_node.right # right
return results
统一迭代
理论基础
迭代方法无法像递归一样以统一框架来处理前中后序遍历,最大的原因是中序遍历的处理与访问时分开的(类似于双指针)。
处理方法是将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记(要处理的节点放入栈之后,紧接着放入一个空指针作为标记。
统一的解法采用先全部记录,再进行处理的思路,用栈先收集所有节点,然后在栈中弹出顺序元素。
不过这种统一的迭代方法的理论意义大,实际使用还是正常用迭代和递归即可。
前序遍历 - 统一
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = [root]
results = []
while (len(stack) > 0):
curr_node = stack.pop()
if curr_node != None:
if curr_node.right != None:
stack.append(curr_node.right) # right
if curr_node.left != None:
stack.append(curr_node.left) # left
stack.append(curr_node) # middle
stack.append(None)
else:
results.append(stack.pop().val)
return results
后序遍历 - 统一
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = [root]
results = []
while (len(stack) > 0):
curr_node = stack.pop()
if curr_node != None:
stack.append(curr_node) # middle
stack.append(None)
if curr_node.right != None:
stack.append(curr_node.right) # right
if curr_node.left != None:
stack.append(curr_node.left) # left
else:
results.append(stack.pop().val)
return results
中序遍历 - 统一
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
if root == None:
return []
stack = [root]
results = []
while (len(stack) > 0):
curr_node = stack.pop()
if curr_node != None:
if curr_node.right != None:
stack.append(curr_node.right) # right
stack.append(curr_node) # middle
stack.append(None)
if curr_node.left != None:
stack.append(curr_node.left) # left
else:
results.append(stack.pop().val)
return results