深度学习基础之卷积（涵盖基本大多数神经网络中会用到的卷积）

大话卷积！！！

首先我们说的卷积是神经网络中的卷积不是信号处理和信号分析里面的卷积，这两者是有区别的。
（部分内容和图片取自https://blog.csdn.net/ahxieqi/article/details/93628533
和公众号GiantPandaCV）

1、1x1卷积

我们都知道卷积核的一个特性就是，输出图像的纬度只取决于卷积核的数量！其实内部原理拿1x1卷积核来举个栗子就是，1x1卷积核相当于一个全连接层，对channel这一维度的信息进行全连接操作，所以能够实现升维或是降维。
1x1卷积核作用
1、降维/升维
2、增加非线性
1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。
3、跨通道信息交互（channal 的变换）

例子：使用1x1卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，3x3，64channels的卷积核后面添加一个1x1，28channels的卷积核，就变成了3x3，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互[7]。

注意：只是在channel维度上做线性组合，W和H上是共享权值的sliding window

2、3D卷积

这里要区分一下，2D和3D，这跟我们想象中的2D和3D不一样。当输入的channel和卷积核的channel一样的时候，这时候就是2D卷积，因为卷积核仅在2D平面移动。而3D卷积就是当输入的channel和卷积核的channel不一样的时候，这时候就是3D卷积。因为这时候卷积核还会在channel这个维度上移动。

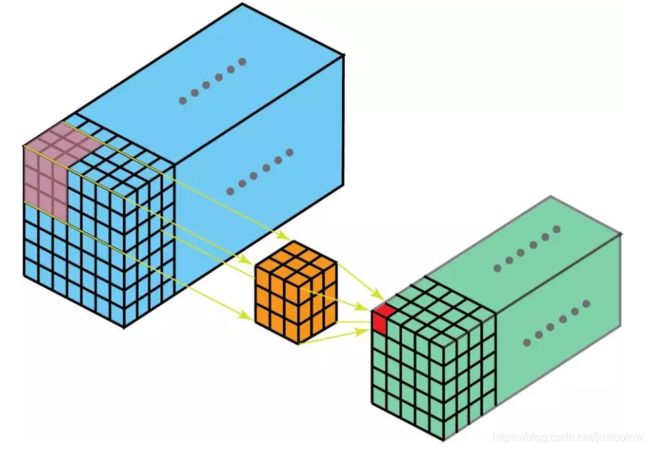
在 3D 卷积中，3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动。在每个位置，逐元素的乘法和加法都会提供一个数值。因为过滤器是滑过一个 3D 空间，所以输出数值也按 3D 空间排布。也就是说输出是一个 3D 数据。

与 2D 卷积（编码了 2D 域中目标的空间关系）类似，3D 卷积可以描述 3D 空间中目标的空间关系。对某些应用（比如生物医学影像中的 3D 分割/重构）而言，这样的 3D 关系很重要，比如在 CT 和 MRI 中，血管之类的目标会在 3D 空间中蜿蜒曲折。

3、转置卷积

转置卷积也就是我们常说的反卷积（FSC）。对于下图的例子，我们在一个 2×2 的输入（周围加了 2×2 的单位步长的零填充）上应用一个 3×3 核的转置卷积。上采样输出的大小是 4×4。

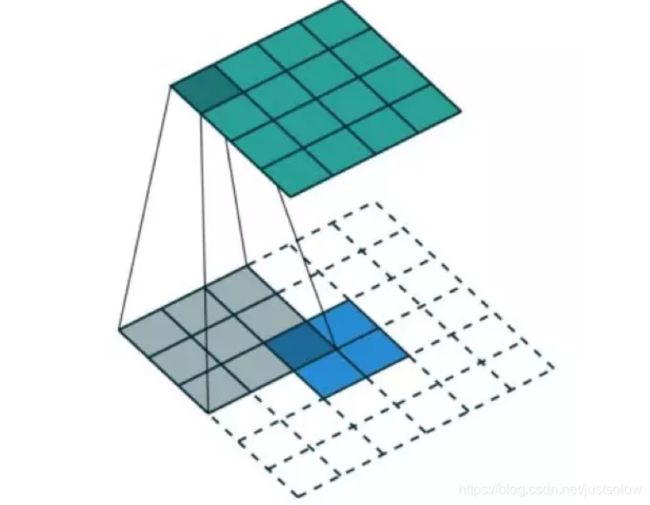
有了直观的了解以后，我们再来看看计算机里面的实现过程，这时候你就可以清楚地知道为什么他会被叫做转置卷积了。
下面的例子展示了这种运算的工作方式。它将输入平展为 16×1 的矩阵，并将卷积核转换为一个稀疏矩阵（4×16）。然后，在稀疏矩阵和平展的输入之间使用矩阵乘法。之后，再将所得到的矩阵（4×1）转换为 2×2 的输出。

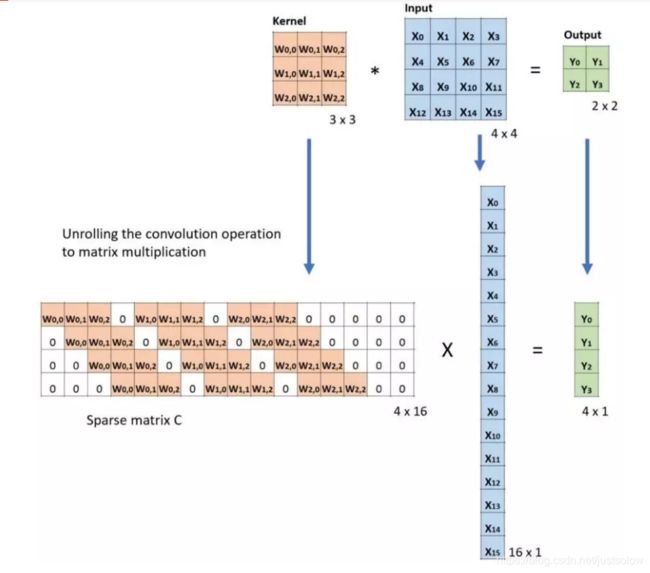
现在，如果我们在等式的两边都乘上矩阵的转置 CT，并借助「一个矩阵与其转置矩阵的乘法得到一个单位矩阵」这一性质，那么我们就能得到公式 CT x Small = Large，如下图所示。

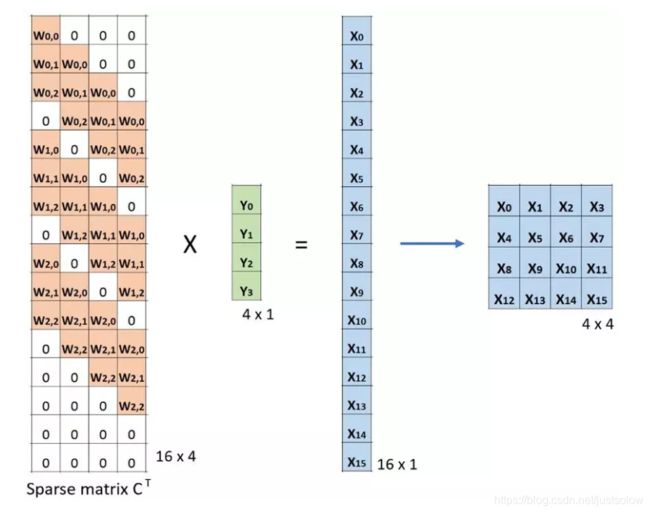
3、深度可分卷积

现在来看深度可分卷积，这在深度学习领域要常用得多（比如 MobileNet 和 Xception）。深度可分卷积包含两个步骤：深度卷积核 1×1 卷积。

在描述这些步骤之前，有必要回顾一下我们之前介绍的 2D 卷积核 1×1 卷积。首先快速回顾标准的 2D 卷积。举一个具体例子，假设输入层的大小是 7×7×3（高×宽×通道），而过滤器的大小是 3×3×3。经过与一个过滤器的 2D 卷积之后，输出层的大小是 5×5×1（仅有一个通道）。

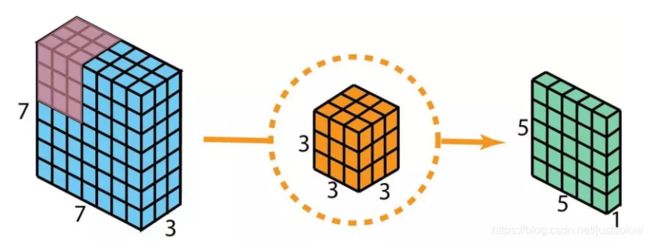
一般来说，两个神经网络层之间会应用多个过滤器。假设我们这里有 128 个过滤器。在应用了这 128 个 2D 卷积之后，我们有 128 个 5×5×1 的输出映射图（map）。然后我们将这些映射图堆叠成大小为 5×5×128 的单层。通过这种操作，我们可将输入层（7×7×3）转换成输出层（5×5×128）。空间维度（即高度和宽度）会变小，而深度会增大。

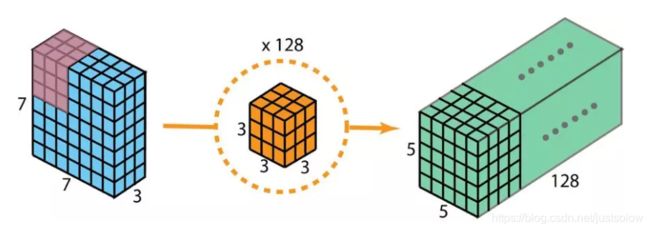
现在使用深度可分卷积，看看我们如何实现同样的变换。

首先，我们将深度卷积应用于输入层。但我们不使用 2D 卷积中大小为 3×3×3 的单个过滤器，而是分开使用 3 个核。每个过滤器的大小为 3×3×1。每个核与输入层的一个通道卷积（仅一个通道，而非所有通道！）。每个这样的卷积都能提供大小为 5×5×1 的映射图。然后我们将这些映射图堆叠在一起，创建一个 5×5×3 的图像。经过这个操作之后，我们得到大小为 5×5×3 的输出。现在我们可以降低空间维度了，但深度还是和之前一样。

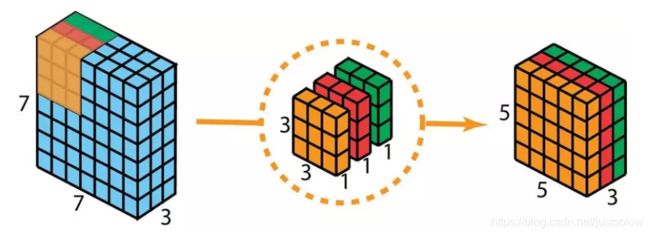
深度可分卷积——第一步：我们不使用 2D 卷积中大小为 3×3×3 的单个过滤器，而是分开使用 3 个核。每个过滤器的大小为 3×3×1。每个核与输入层的一个通道卷积（仅一个通道，而非所有通道！）。每个这样的卷积都能提供大小为 5×5×1 的映射图。然后我们将这些映射图堆叠在一起，创建一个 5×5×3 的图像。经过这个操作之后，我们得到大小为 5×5×3 的输出。

在深度可分卷积的第二步，为了扩展深度，我们应用一个核大小为 1×1×3 的 1×1 卷积。将 5×5×3 的输入图像与每个 1×1×3 的核卷积，可得到大小为 5×5×1 的映射图。

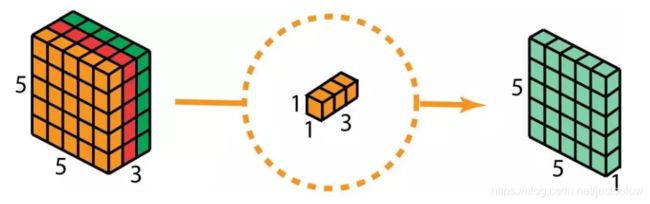
因此，在应用了 128 个 1×1 卷积之后，我们得到大小为 5×5×128 的层。

下图展示了深度可分卷积的整个过程。

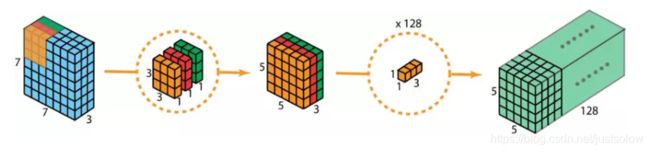
这样做极大的提升了计算的效率，节省了计算资源。

5、分组卷积

看图应该就懂了，分开卷积在合并么。

6、平展卷积

也是看图基本几句可以了解了，分别在C,H,W三个维度上拆分卷积。

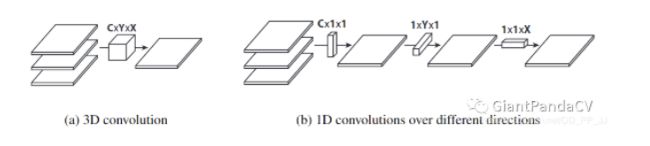
论文在结论中提到，使用Flattened Convolutions能够将计算量减少为原来的10倍，并可以达到类似或更高的准确率在CIFAR-10、CIFAR-100和MNIST数据集中。

深度学习中的学习型滤波器具有分布特征值，直接将分离应用在滤波器中会导致严重的信息损失，过多使用的话会对模型准确率产生一定影响。

7、DCN可变性卷积

DCN提出的动机是为何特征提取形状一定要是正方形或者矩形，为何不能更加自适应的分布到目标上（如下图右侧所示），进而提出了一种形状可学习的卷积。

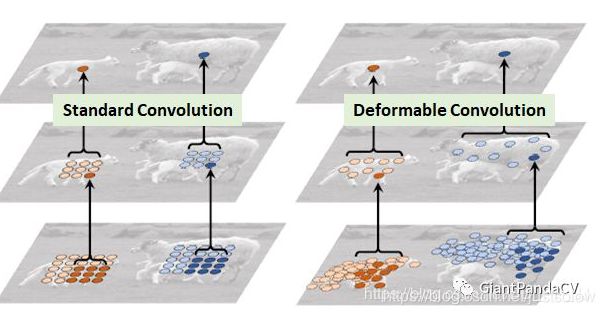
实现过程如下图所示，在普通卷积之外又添加了一个分支，专门用于学习每个点的偏移量，将原始的卷积和offset结合就形成了可变形卷积。

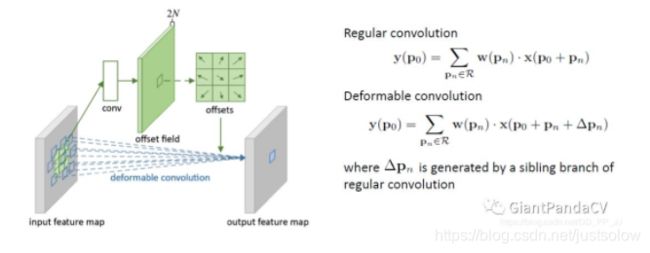
8. Attention

（1）这里介绍两个最经典的注意力机制的模块，SE Module和CBAM Module。
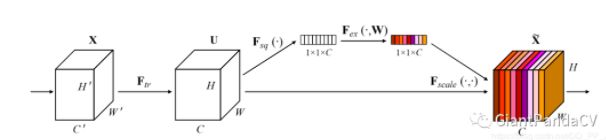
SENet的核心想法是，每个通道的重要性不是一样的。基于这个想法，SENet添加了一个模块，如上图靠上的分支，这个模块作用是给每个通道打分，最终将打分的结果与卷积得到的feature map相乘，完成特征通道的权重重分配。SENet是通道注意力机制的最经典的实现。

pytorch实现：

class SELayer(nn.Module):
    def __init__(self, channel, reduction=16):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
            nn.Linear(channel, channel // reduction, bias=False),
            nn.ReLU(inplace=True),
            nn.Linear(channel // reduction, channel, bias=False),
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y.expand_as(x)

缺点：不利于并行处理，添加SELayer以后导致在GPU上运行速度有一定的减慢。
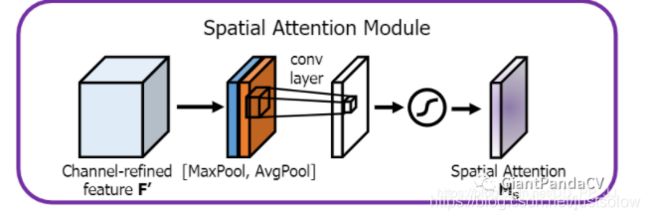
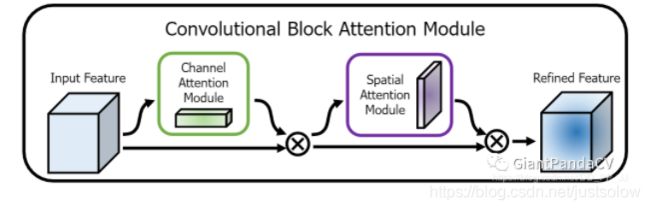
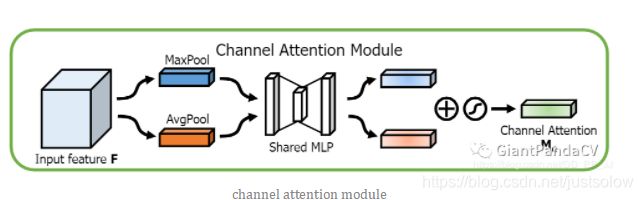
（2）CBAM模块算是比较早的一批将通道注意力机制和空间注意力机制结合起来的模型，通过添加该模块，能在一定程度上优化feature。

CBAM分为Channel Attention Module 和 Spatial Attention Module:

相关代码（还是代码好理解）：

class ChannelAttention(nn.Module):
    def __init__(self, in_planes, rotio=16):
        super(ChannelAttention, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.max_pool = nn.AdaptiveMaxPool2d(1)

        self.sharedMLP = nn.Sequential(
            nn.Conv2d(in_planes, in_planes // ratio, 1, bias=False), nn.ReLU(),
            nn.Conv2d(in_planes // rotio, in_planes, 1, bias=False))
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avgout = self.sharedMLP(self.avg_pool(x))
        maxout = self.sharedMLP(self.max_pool(x))
        return self.sigmoid(avgout + maxout)

class SpatialAttention(nn.Module):
    def __init__(self, kernel_size=7):
        super(SpatialAttention, self).__init__()
        assert kernel_size in (3,7), "kernel size must be 3 or 7"
        padding = 3 if kernel_size == 7 else 1

        self.conv = nn.Conv2d(2,1,kernel_size, padding=padding, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avgout = torch.mean(x, dim=1, keepdim=True)
        maxout, _ = torch.max(x, dim=1, keepdim=True)
        x = torch.cat([avgout, maxout], dim=1)
        x = self.conv(x)
        return self.sigmoid(x)

最终CBAM模块选择将两个部分进行串联：

9、空洞卷积（dalited conv）

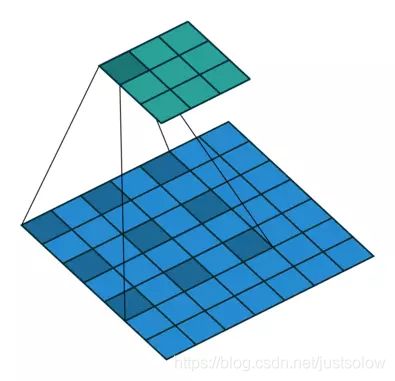
Deep CNN 对于其他任务还有一些致命性的缺陷。较为著名的是 up-sampling 和 pooling layer 的设计。
主要问题有：

1、Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic. (参数不可学习)
2、内部数据结构丢失；空间层级化信息丢失。
3、小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)

在这样问题的存在下，语义分割问题一直处在瓶颈期无法再明显提高精度， 而 dilated convolution 的设计就良好的避免了这些问题。

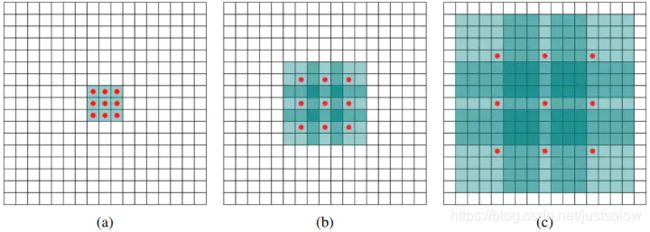
(a)图对应3x3的1-dilated conv，和普通的卷积操作一样，(b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3x3，但是这个卷积的感受野已经增大到了7x7（如果考虑到这个2-dilated conv的前一层是一个1-dilated conv的话，那么每个红点就是1-dilated的卷积输出，所以感受野为3x3，所以1-dilated和2-dilated合起来就能达到7x7的conv）,©图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15x15的感受野。对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到(kernel-1)*layer+1=7的感受野，也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。

空洞卷积存在的问题
潜在问题 1：The Gridding Effect

假设我们仅仅多次叠加 dilation rate 2 的 3 x 3 kernel 的话，则会出现这个问题：

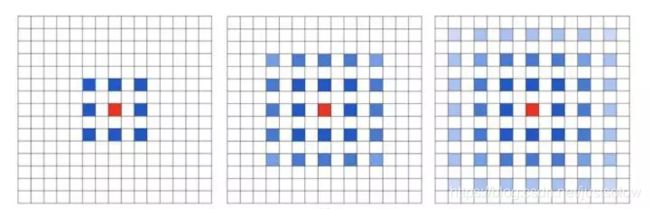
我们发现我们的 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。

潜在问题 2：Long-ranged information might be not relevant.

我们从 dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而光采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了。如何同时处理不同大小的物体的关系，则是设计好 dilated convolution 网络的关键。

总结：

卷积核的设计非常多，以上仅仅是一部分常见的卷积核，以上卷积核可以这样分类：

通道和空间

Convolution
1x1 Convolution
Spatial and Cross-Channel Convolutions
通道相关性（channel）

Depthwise Separable Convolutions
Shuffled Grouped Convolutions
Squeeze and Excitation Network
Channel Attention Module in CBAM
空间相关性（HxW）

Spatially Separable Convolutions
Flattened Convolutions
Dilated Convolutions
Deformable Convolution
Spatial Attention Module in CBAM