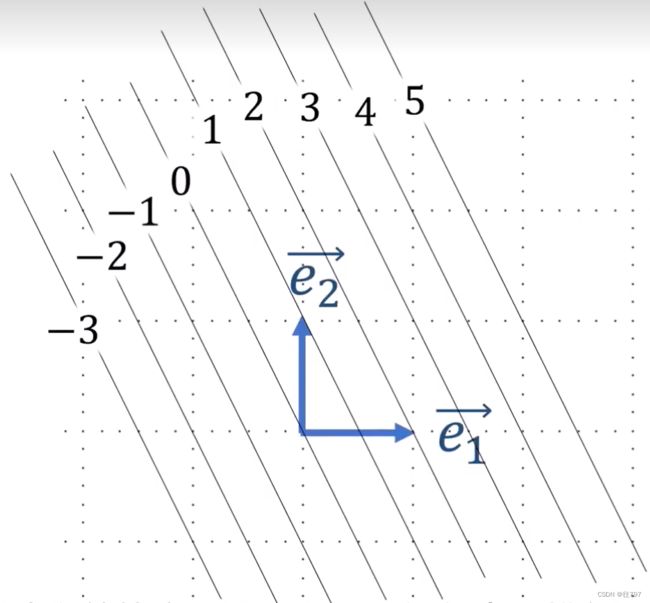
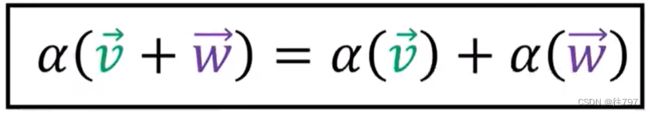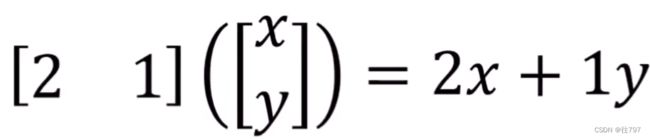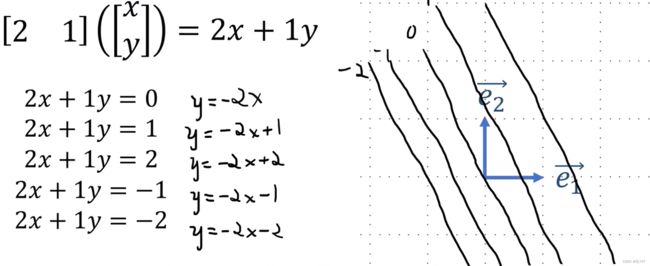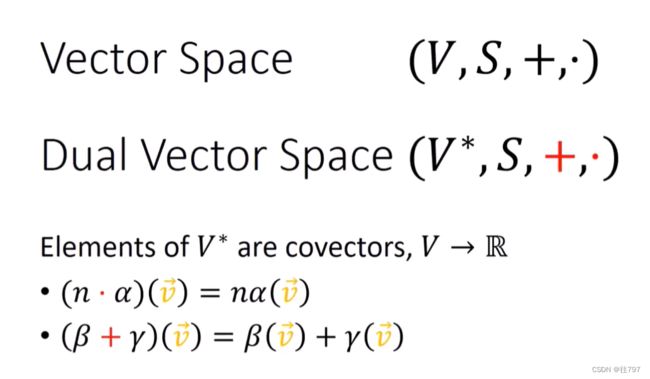6.Tensors For Beginners-What are Convector
Covectors (协向量)
What‘s a covector
Covectors are “basically” Row Vectors
在一定程度上,可认为 协向量 基本上就像 行向量。
但不能简单地认为 这就是列向量进行转置!
行向量 和 列向量 是根本不同类型的对象。
(处理正交基时,将列向量转置成行向量的做法是正确的,但在其他坐标系中不是这样)
要理解这个,需将 行向量视为函数,
因此,可将行向量 视为 列向量上的函数,row vectors are functions on (column) vectors
eg:y=f(x) x就是输入
行向量 [ 2,1 ]是函数,列向量 [ -3 ; 4 ]是函数的输入,
要得到函数的输出值,只需对该行向量和列向量进行矩阵乘法 或“点积”
现如果,有 任意通用的协向量α 作用于 任意通用向量v上,
则可通过两向量的点积来获取输出值,
因此,最终我们应将 行向量 视为 【从某个向量空间V 中 获取输入并返回实数或“标量”】的函数
这些行向量函数是如何工作的?
假设一行向量 作用于两个相加的向量输入上,可通过两种方式求,
(1.分配律--我认为就是分配律的体现)
将行向量分配给每个输入,然后将结果相加,输出
所以行向量作为函数 在这里有个属性:可以在之前添加输入;或在之后添加输出。会得到相同的结果
还有一个想法是:
若向量输入按某个数字进行缩放会怎样
同样有两种方法计算
2.把缩放数 提到最前面,再计算行向量与列向量的点积,最后再缩放结果,
因此,作为函数的行向量具有这个属性:可缩放输入,或缩放输出,并得到相同的结果。
总而言之, 协向量是一个 函数,它接受一个向量并产生一个“标量”(或一个数字);它具有可添加输入或添加输出以获得相同答案的属性;并且它具有可按相同数量缩放输入或缩放输出并得到相同答案的属性。
这种能添加或缩放 输入或输出 并获得相同答案的行为 称为 “线性“。所以协向量是线性函数。
如何可视化协向量?
我们可以将普通向量可视化为箭头,我们可以对协向量做同样的事情,但对于可视化函数来说,这是件尴尬的事。
有一种更好的办法可视化协向量
首先将2D行向量视为两个变量x、y的函数,(x、y是输入)
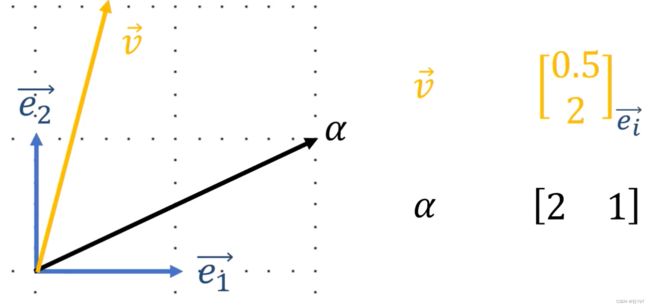
在这个例子中,这个行向量 [ 2 , 1 ] 就可认为是一个函数:v,如何可视化 用两个变量产生一个输出 的函数 呢?
这与地形图有些相似,地形图上,同一海拔高度的都用一条线连起来。
同样地,我们给这个函数一个输出,就有一条线,
如 2x+1y = 0 确定一条线;
2x+1y = 1 确定一条线;
2x+1y = 2 确定一条线;
2x+1y = -1 确定一条线;
2x+1y = -2 确定一条线;
所以我们可将协向量【2,1】视为 一堆的直线:
注意到,这些线 向右上角增加,可添加箭头提示增加的方向。
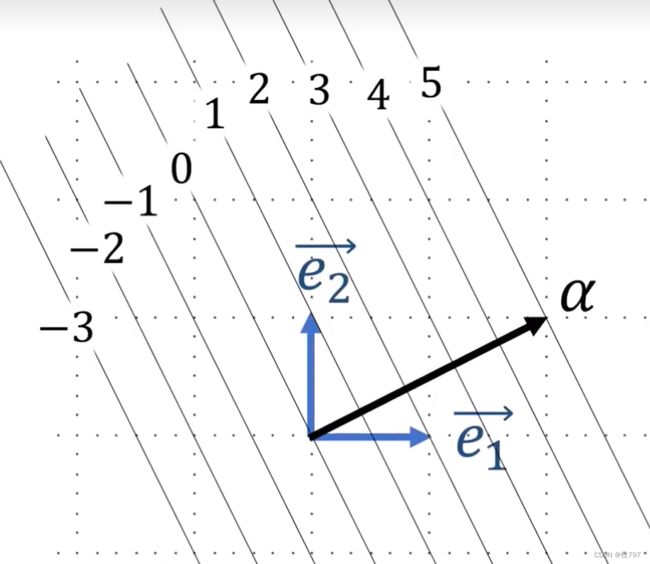
将行向量α=【2,1】绘制在图上的话,会发现 α 垂直于 所有的直线。
为什么会垂直?把【2,1】用【a,b】去进行证明,一个方向是 这些直线的方向相同,方向向量相同,用方向向量与α进行点乘; 另一个方向是 斜率,直线的斜率都一样(-a/b),α行向量作为直线的话,斜率是b/a,也可证明
所以我们可将协向量【2,1】视为 一堆的直线,而且这非常有用。
例子:
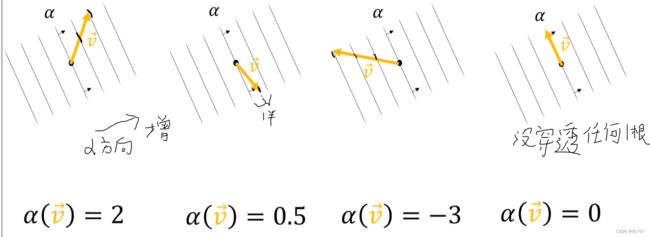
在这四个图中,协向量α相同,可视化为一堆线
在该协向量上, 有向量V指向不同的方向,
记住:这一堆线中的每一条线都是代表一常量值的线,
因此,要获得作用在V上的α的值,需要做的是 计算V穿透的线的个数。
PS:这样计算真的好简单,但是对于编写成代码来计算的话,好像很难把,想不出头绪,能自己画出图,这样是最直观,但画图也不容易。
接着,修改协向量,获得新的协向量来进行计算
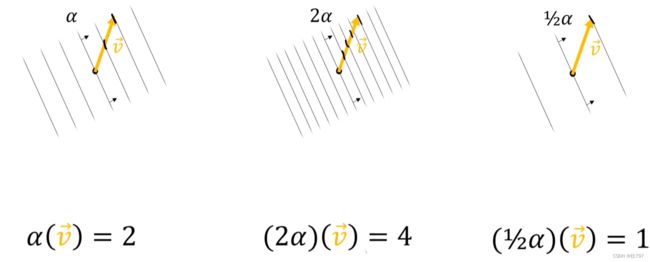
把协向量放大两倍
把协向量放大两倍,其实就是从 α 变为 2α , 如果你从式子上看的话, 能直接想到应该是结果放大两倍, 那么对应的输出结果应该放大两倍, 那对应图上,就是穿透的线要翻倍,则图要变密集,比原来密集一倍。
从 【a,b】*【x;y】上理解,ax+by函数,变为【2a,2b】*【x;y】= 2ax + 2by、ax+by = k---------y = -ax/b + k/b;
2ax+2by= k-------y= -ax/b + k/2b; 只是截距变啦,斜率没变, 所以截距影响线 的间距?
以上就是缩放协向量;
接着便是把协向量进行相加的情况,
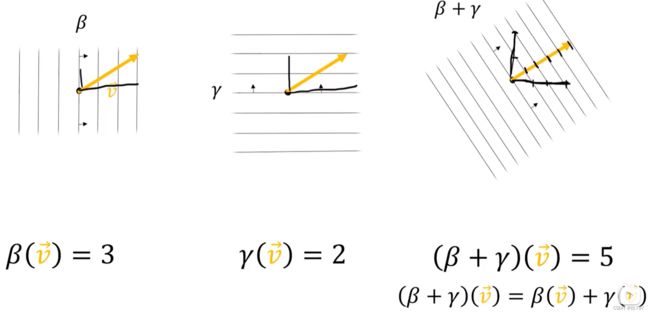
β、γ两个协向量进行相加,如何画出β+γ的线?----------结果 在 β方向上与β具有相同的密度,在γ方向上与γ具有相同的密度。
观察相加后的新协向量,V在β方向上的分量 同之前一样,穿透三根线,V在γ方向上的分量 同之前一样,穿透两根线。
从某种意义上说,β的水平密度为3,垂直密度为0;而γ的水平密度为0,垂直密度为2
而β+γ ,就是将两者结合在一起,水平密度:3+0=3;垂直密度:0+2 =2
而V在β+γ这个协向量上穿透5根线,其实就是原来的:V在β上穿透3根,在γ上穿透2根,加起来就是5根。,
其实从式子上理解的话,是非常容易理解的。
以上就证明,协向量具有合理的缩放和添加规则,
作用于向量V的所有covector 的集合形成一个新的向量空间,称为”对偶空间“,用 ” V* “表示,
有一组不同的添加规则,称为”red+“ ---- ” + “
有一组不同的缩放规则,称为”red·“------” · “
用不同颜色来表示这些规则的原因是 因为它们实际上是不同的规则,
黑色规则用于添加和缩放向量,就是用箭头表示的矢量所作规则;
红色规则用于添加和缩放协向量,像上面的例子那般,
V* 中的元素就是协向量,它们是 从V到实数的函数,
总结。协向量是从向量到实数的函数 , 这些函数具有可以添加和缩放输入 或 添加和缩放输出 以获得相同答案的属性。这就是所谓的”线性“,所以这些是线性函数。
作用在向量空间 V 上的所有协向量的集合形成 向量空间V*,这些协向量有自己的加法和缩放规则,可将协向量视为 一簇线,
+