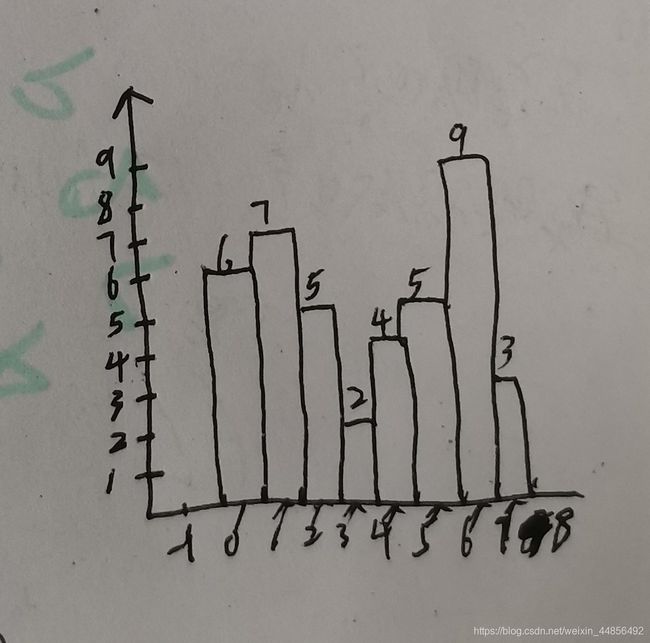【刷题】不同专题篇
小文目录:
-
-
- 1、递归
-
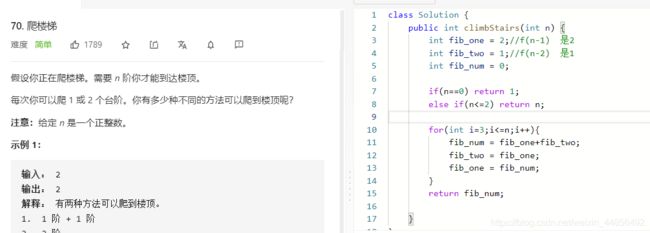
- L70:爬楼梯(斐波那契数列)
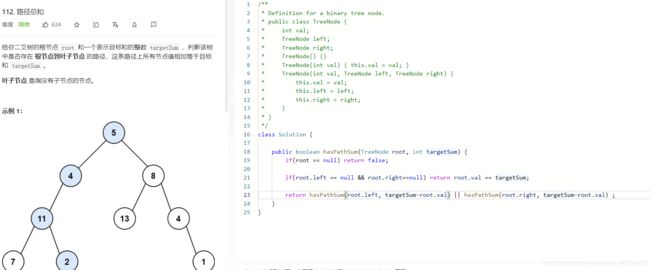
- L112:路径总和
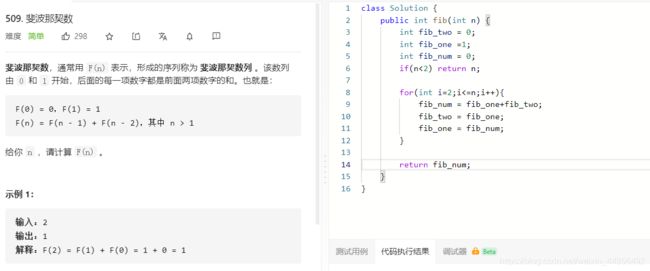
- L509:斐波那契数列
- 2、分治
-
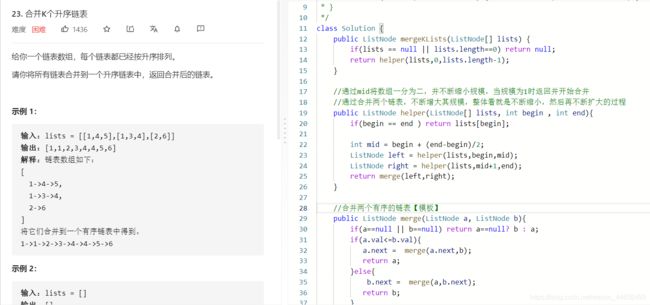
- L23:合并K个升序链表
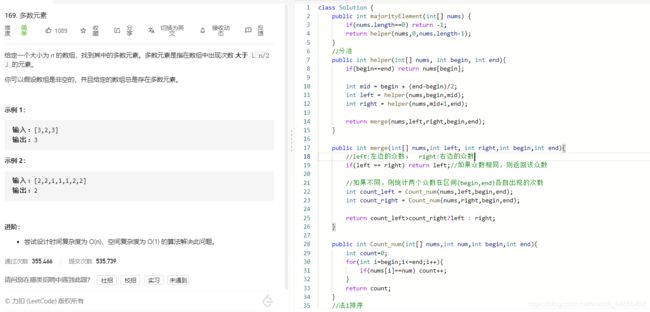
- L169:多数元素(超过一半的数字)
- 3、单调栈
-
- L84:柱状图中最大矩形
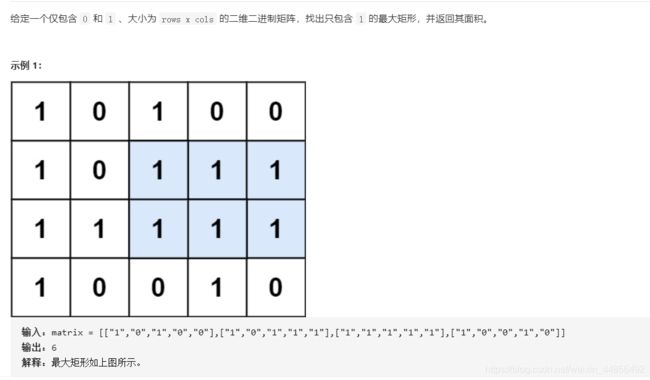
- L85:最大矩形
- L739:每日温度
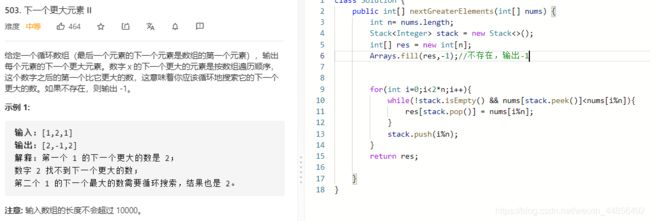
- L503: 下一个更大的元素
- 4、并查集
- 5、滑动窗口
-
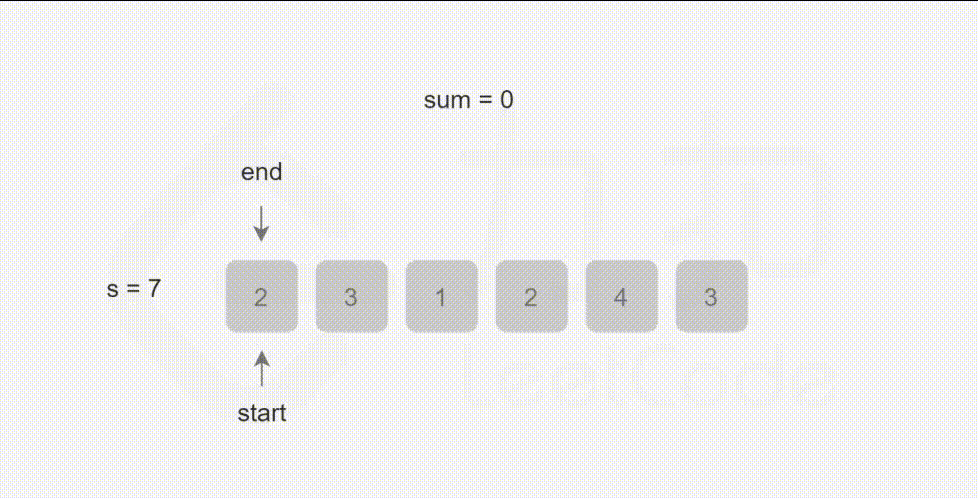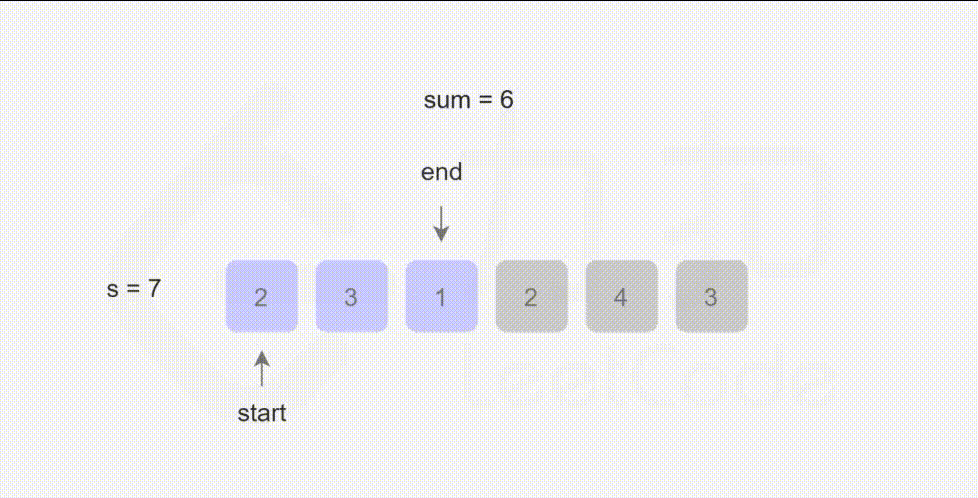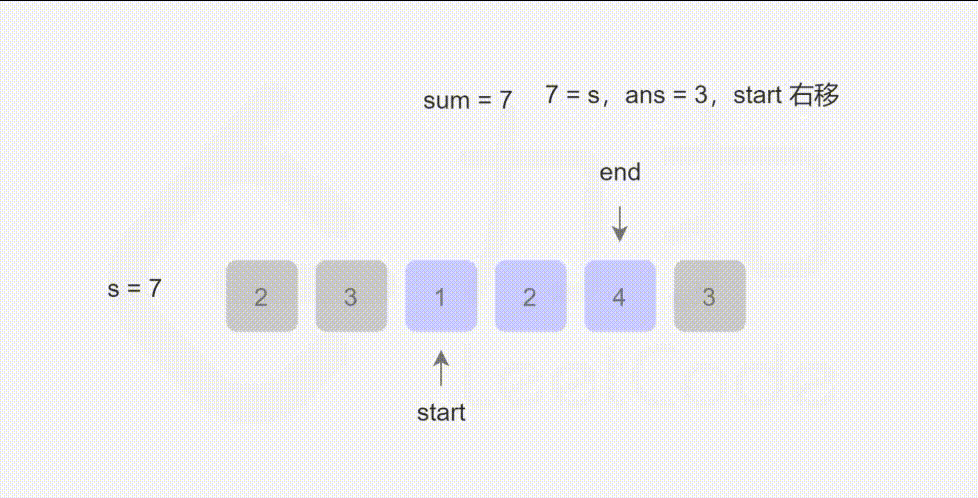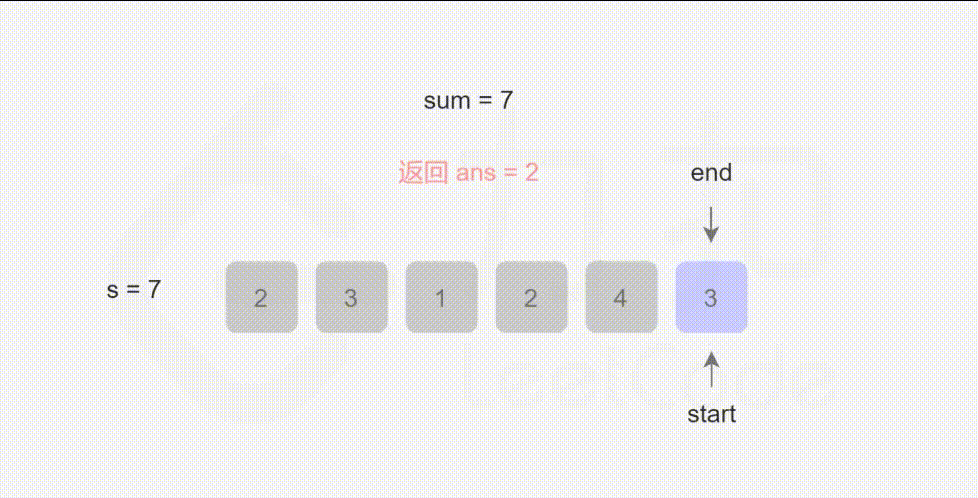
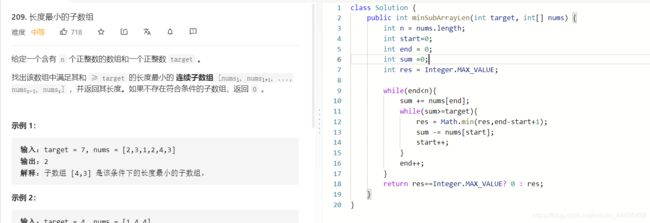
- L209:长度最小的子数组
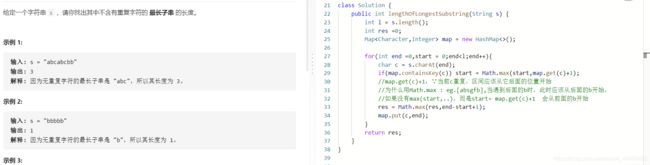
- L3:无重复字符的最长子串
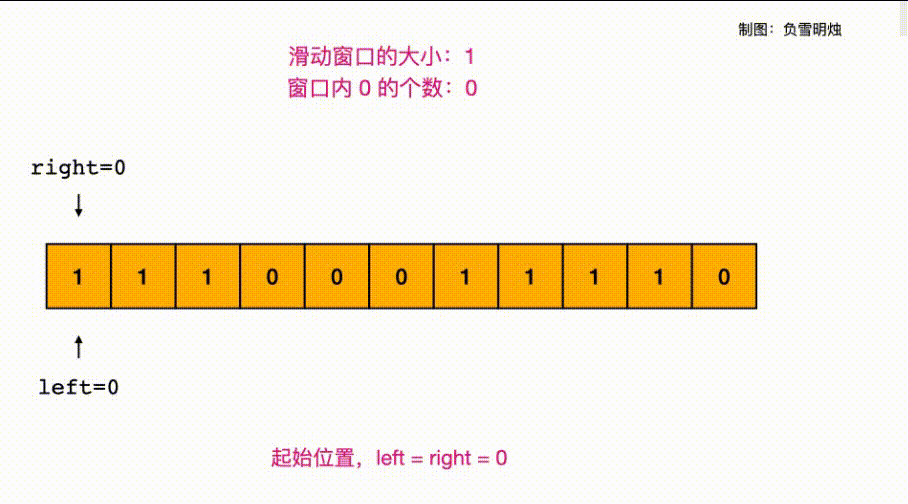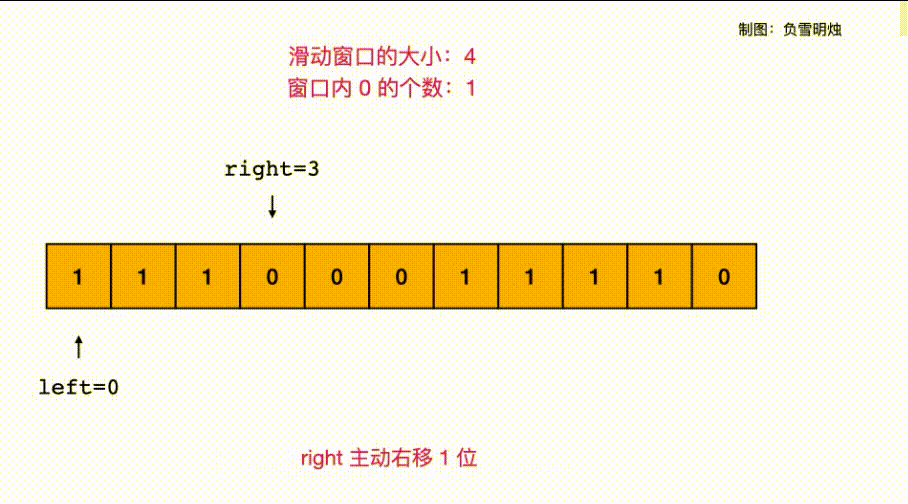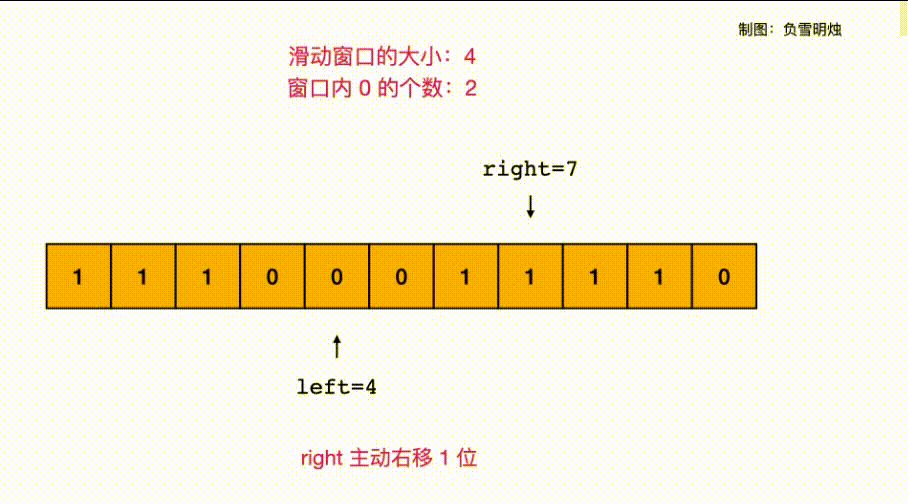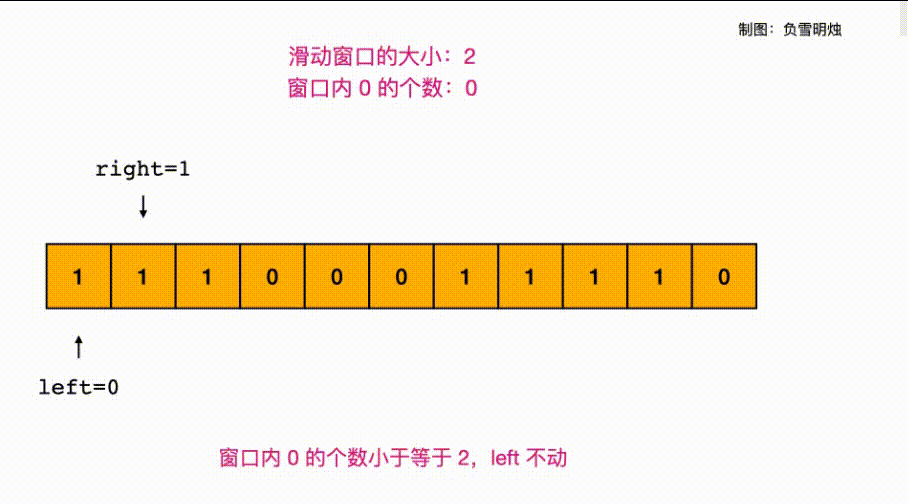
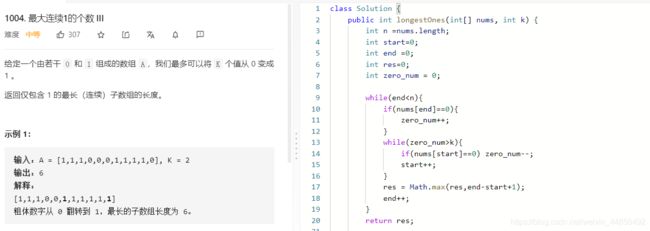
- L1004:最大连续1的个数 III
- 6、前缀和
-
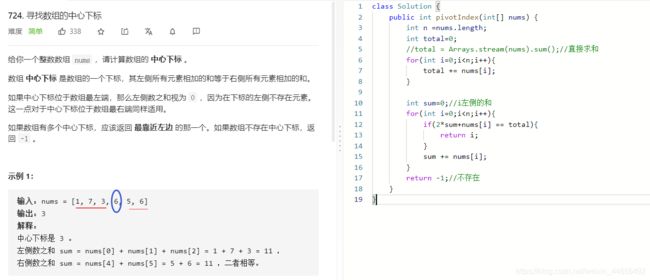
- L724:寻找数组的中心下标
- L560:和为K的子数组
- L437:路径总和 III
- L1248:统计优美子数组
- 7、拆分(差分)
-
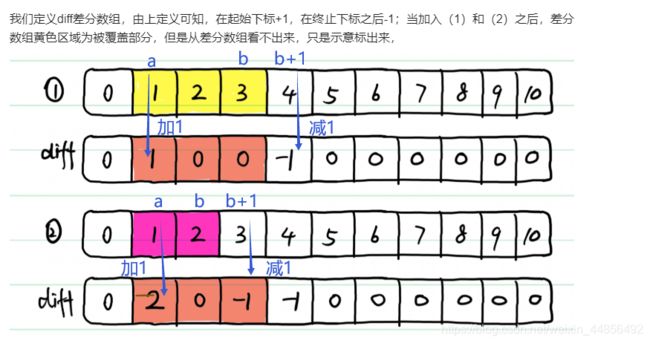
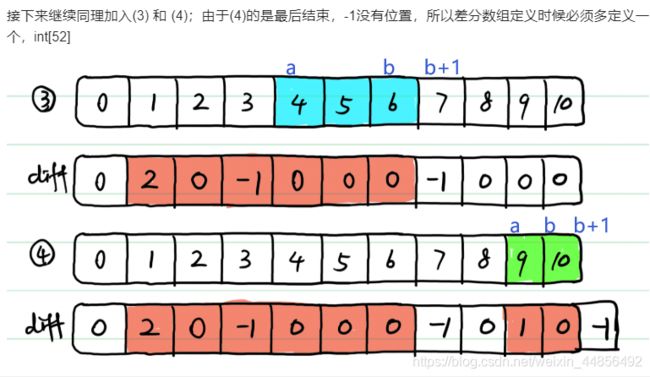
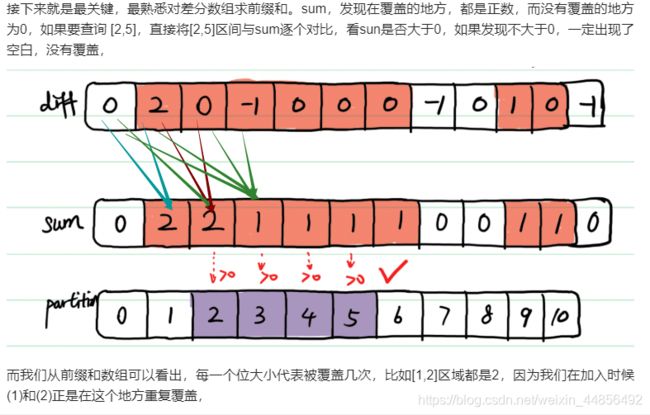
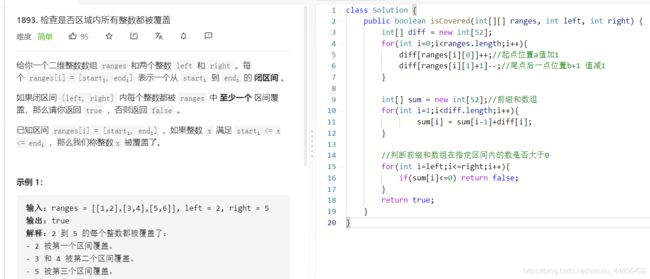
- L1893:检查是否区域内所有整数都被覆盖
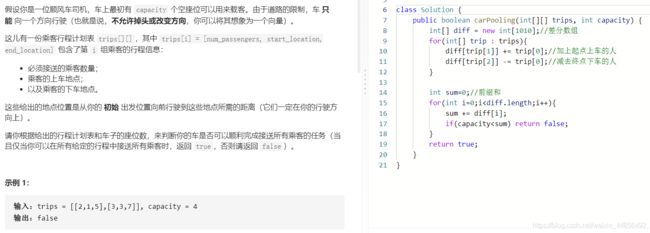
- L1094:拼车
- 8、拓扑排序
-
- L210:课程表 II
- 9、字符串
-
- L5:回文子串
- L20:有效括号
- L43:字符串相乘
- 10、二分查找
-
- L33:搜索旋转排序数组
- L34:在排序数组中查找元素的第一个和最后一个位置
- 11、BFS
- 12、DFS&回溯
- 13、动态规划
- 14、贪心
- 15、字典树
-
递归: LeetCode70、112、509
分治: LeetCode23、169、240
单调栈: LeetCode84、85、739、503
并查集: LeetCode547、200、684
滑动窗口:LeetCode209、3、1004、1208
前缀和: LeetCode724、560、437、1248
差分: LeetCode1094、121、122
拓扑排序:LeetCode210
字符串: LeetCode5、20、43、93
二分查找:LeetCode33、34
BFS: LeetCode127、139、130、529、815
DFS&回溯::LeetCode934、685、1102、531、533、113、332、337
动态规划:LeetCode213、123、62、63、361、1230
贪心算法:LeetCode55、435、621、452
字典树: LeetCode820、208、648
1、递归
L70:爬楼梯(斐波那契数列)
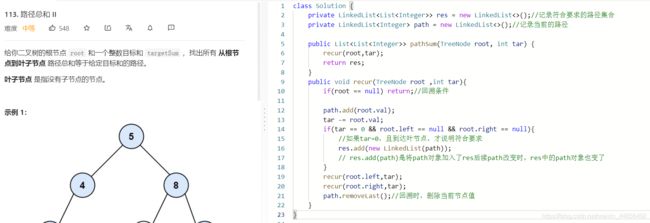
L112:路径总和
L509:斐波那契数列
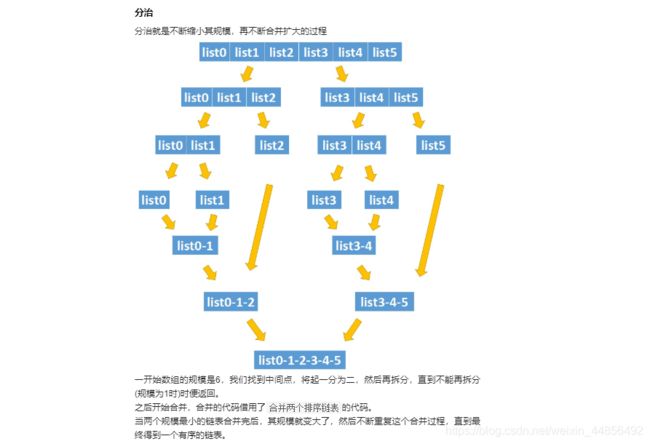
2、分治
L23:合并K个升序链表
L169:多数元素(超过一半的数字)
3、单调栈
单调栈:判别是否需要使用单调栈,如果需要找到左边或者右边第一个比当前位置的数大或者小,则可以考虑使用单调栈
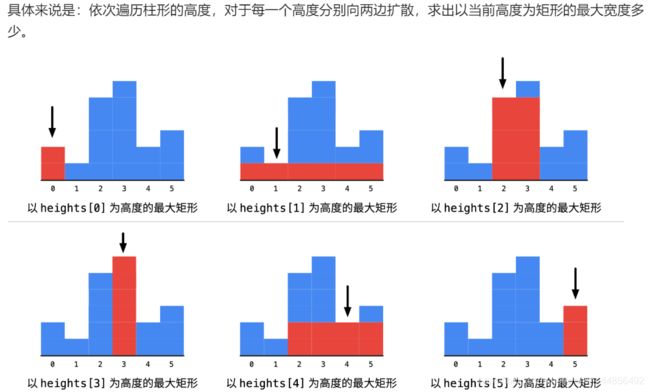
L84:柱状图中最大矩形

上文中,定义了-1和8。表示当前柱子左侧/右侧最近的柱子没有比自己低的,故高度还是本身。
例如:[-1,0,-1,-1,3,4,5,3],当中的-1表示第0、2、3号柱子各自的左边(从左往右依次遍历时)都没有比自己低的柱子;[2,2,3,8,7,7,7,8]当中的8表示第7、3号柱子各自的右边(从右往左依次遍历时)都没有比自己低的柱子。
其他数字表示:例如[-1,0,-1,-1,3,4,5,3]中的0表示索引1号柱子左边离他最近比他低的柱子编号是0;5表示索引6号的柱子左边离他最近比他低的柱子编号是5;
例如[2,2,3,8,7,7,7,8]中的3表示索引2号的柱子右边最近比他低的是3号;
代码:
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
Stack<Integer> stack = new Stack<>();
int[] left = new int[n];//记录从左到右每个柱子的左边离他最近的比他低的柱子编号
int[] right = new int[n];//记录从右到左每个柱子的右边离他最近的比他低的柱子编号
//找左边的
for(int i =0;i<n;i++){
while(!stack.isEmpty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
left[i] = stack.isEmpty()? -1 : stack.peek();
stack.push(i);
}
stack.clear();
//找右边的
for(int i =n-1;i>=0;i--){
while(!stack.isEmpty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
right[i] = stack.isEmpty()? n : stack.peek();
stack.push(i);
}
//计算面积
int res =0;
for(int i=0;i<n;i++){
res=Math.max(res,(right[i]-left[i]-1)*heights[i]);//为什么是减1不是+1?
}
return res;
}
}
L85:最大矩形
代码:
class Solution {
public int maximalRectangle(char[][] matrix) {
if(matrix.length==0) return 0;
int[] heights = new int[matrix[0].length];//记录matrix每一列连续是1的高度
int ans=0;
//计算每一列的高度,即连续是1的高度
for(int i=0;i<matrix.length;i++){
//遍历每一列,更新高度
for(int j=0;j<matrix[0].length;j++){
if(matrix[i][j] == '1'){
heights[j] += 1;
}else heights[j] =0;
//这里是清空heights[j],而不是会保留上次的值;因为高度需要连续,即连续的1,只要中间有一个是0,则高度从0开始重新累计
}
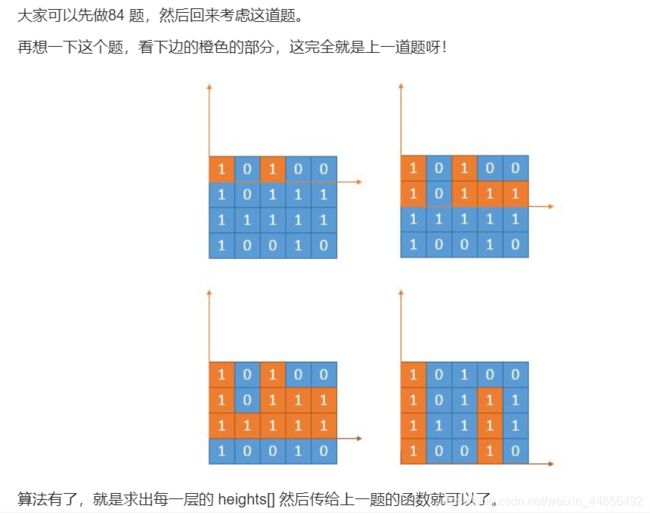
ans =Math.max(ans,largeRecetangle(heights));//将计算好的heights送到84题,求heights[]的最大矩形面积
}
return ans;
}
public int largeRecetangle(int[] heights){
int n = heights.length;
int[] left =new int[n];
int[] right =new int[n];
Stack<Integer> stack = new Stack<>();
for(int i=0;i<n;i++){
while(!stack.isEmpty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
left[i] = stack.isEmpty()? -1: stack.peek();
stack.push(i);
}
stack.clear();
for(int i=n-1;i>=0;i--){
while(!stack.isEmpty() && heights[stack.peek()]>=heights[i]){
stack.pop();
}
right[i] = stack.isEmpty()? n: stack.peek();
stack.push(i);
}
int res = 0;
for(int i=0;i<n;i++){
res = Math.max(res,(right[i]-left[i]-1)*heights[i]);
}
return res;
}
}
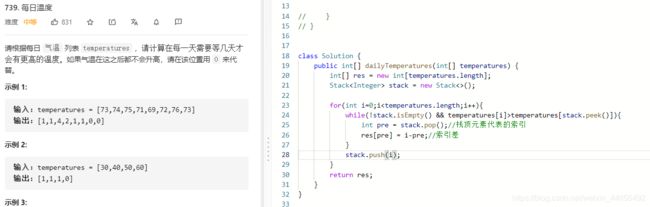
L739:每日温度
L503: 下一个更大的元素
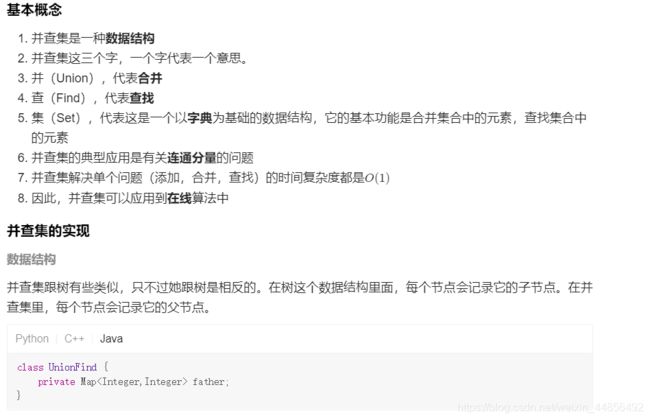
4、并查集
就是集合,能够快速合并,能够快速查询两个节点是否在同一集合中的一种数据结构。一般用树(数组)实现。(并查集基本上可以用DFS、BFS来解决)
5、滑动窗口
L209:长度最小的子数组
L3:无重复字符的最长子串
L1004:最大连续1的个数 III
6、前缀和
L724:寻找数组的中心下标
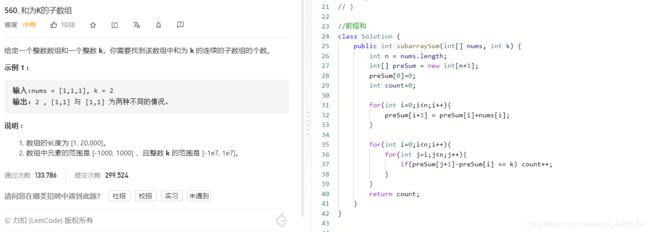
L560:和为K的子数组
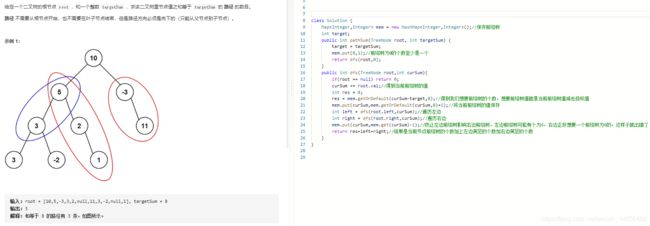
L437:路径总和 III
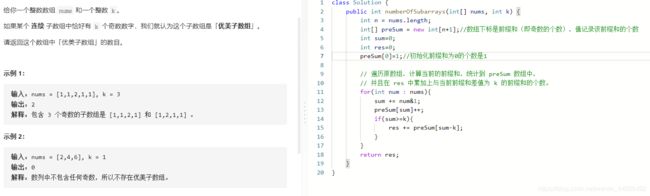
L1248:统计优美子数组
7、拆分(差分)
L1893:检查是否区域内所有整数都被覆盖
L1094:拼车
8、拓扑排序
拓扑排序实际上应用的是贪心算法,贪心算法简而言之:每一步最优,则全局最优。
拓扑排序保证了每个活动(如“课程”)的所有前驱活动都排在该活动的前面,并且可以完成所有活动。
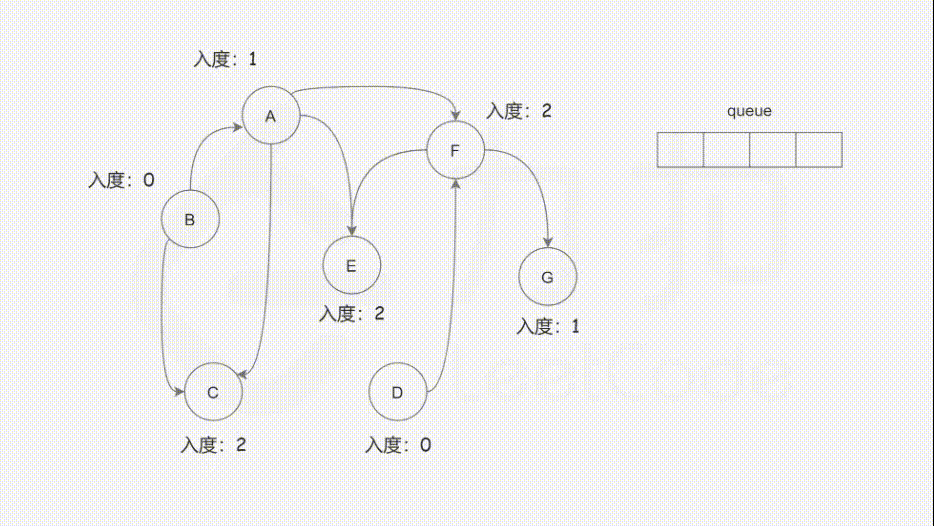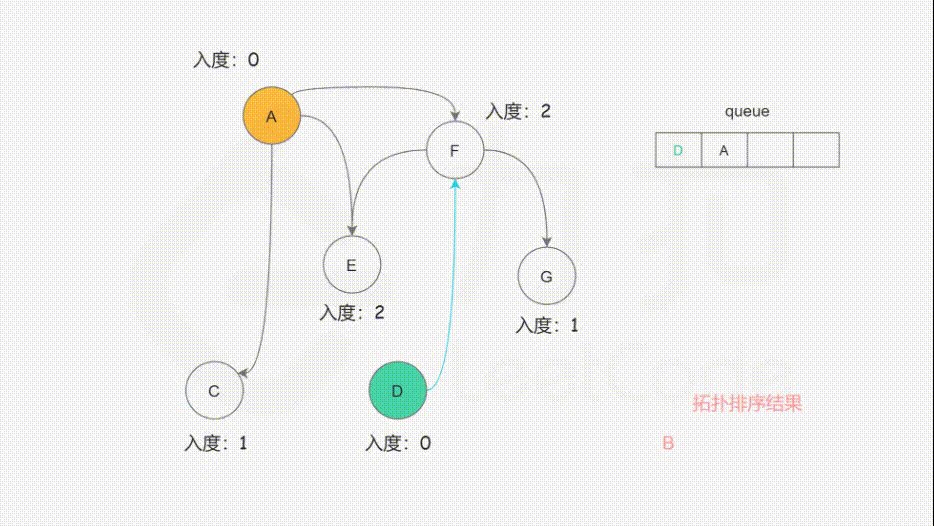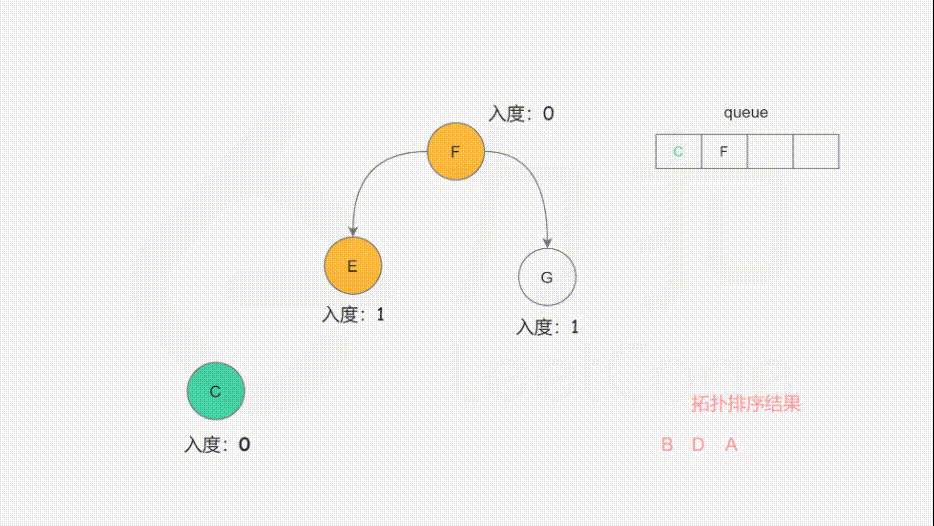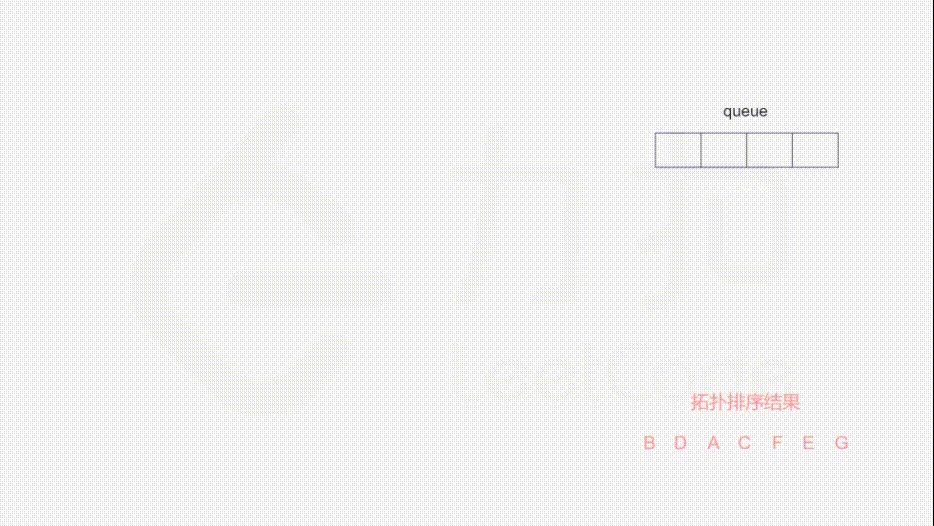
L210:课程表 II
入度:指向当前节点的边,有几条入度就是几
class Solution {
List<List<Integer>> edegs;//存储有向图
int[] indeg;//存储每个节点的入度(即指向该节点的点的个数)
int[] res;//存储答案
int index;//答案的下标,用来循环后移
public int[] findOrder(int numCourses, int[][] prerequisites) {
edegs = new ArrayList<List<Integer>>();
for(int i=0;i<numCourses;i++){
edegs.add(new ArrayList<>());//初始化,先给每个点创造边
}
indeg = new int[numCourses];
res = new int[numCourses];
index = 0;
for(int[] info : prerequisites){
//info存储每个点的矩阵[a,b],a表示当前课程,b表示a前面需有的课
edegs.get(info[1]).add(info[0]);
//给当前点的须有点b(info[1])添加边,指向当前点a(info[0])
indeg[info[0]]++;//当前点的入度+1
}
Queue<Integer> queue = new LinkedList<Integer>();
//将所有入度为0的节点添加到队列当中
for(int i=0;i<numCourses;i++){//∵拓扑排序有多种结果,所以这些节点入队的顺序没有要求
if(indeg[i]==0) queue.offer(i);
}
while(!queue.isEmpty()){
int u = queue.poll();//从队首取出一个节点
res[index++] = u;//加入到结果集
for(int v : edegs.get(u)){//找到u节点的邻接点v
indeg[v]--;//v的入度-1
if(indeg[v] == 0){
queue.offer(v);
}
}
}
if(index!=numCourses) return new int[0];
return res;
}
}
9、字符串
L5:回文子串
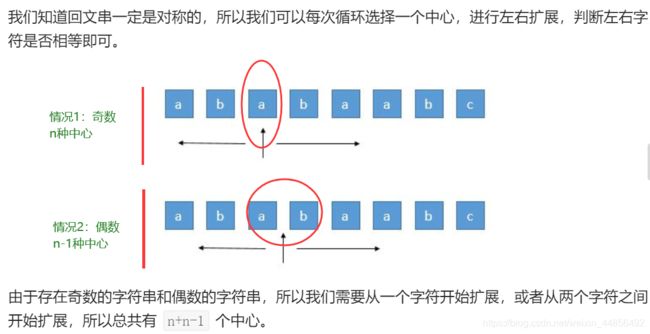
思路:中心扩展法
假设字符串的每个字符为一种初始中心,然后分别向这个字符左右两侧扩展,即判断两边的字符是否相同。如果两边的字母相同,我们就可以继续扩展;如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。我们枚举所有的「回文中心」并尝试「扩展」,直到无法扩展为止,此时的回文串长度即为此「回文中心」下的最长回文串长度。我们对所有的长度求出最大值,即可得到最终的答案。
例如:str = acdbdaastr=acdbbdaa,当中心索引是3时,对应字符b,然后分别从其两边扩展,d==d、c!=a,结束,返回长度3
代码:
class Solution {
public String longestPalindrome(String s) {
if (s == null || s.length() < 1){
return "";
}
// 初始化最大回文子串的起点和终点
int start = 0;
int end = 0;
// 遍历每个位置,当做中心位
for (int i = 0; i < s.length(); i++) {
// 分别拿到奇数偶数的回文子串长度
int len_odd = expandCenter(s,i,i);//情况1、当子串中心是一个字符,eg.abcba 中心是c
int len_even = expandCenter(s,i,i + 1);//情2、当子串中心是两个字符eg.abccba中心是cc
// 对比最大的长度
int len = Math.max(len_odd,len_even);
// 计算对应最大回文子串的起点和终点
if (len > end - start){
//eg.len=12(偶数,说明中间两个字符作为中心),i=6,则start=i-5=1;end=i+6=12;
// 区间为[1,12],中心位置是i=6、7
//eg.len= 1(奇数,说明中间1个字符作为中心),i=6,则start=i-5=1;end=i+5=11;
// 区间为[1,11],中心位置是i=6
start = i - (len - 1)/2;
end = i + len/2;
}
}
// 注意:这里的end+1是因为 java自带的左闭右开的原因
return s.substring(start,end + 1);
}
private int expandCenter(String s,int left,int right){
// left = right 的时候,此时回文中心是一个字符,回文串的长度是奇数
// right = left + 1 的时候,此时回文中心是一个空隙,回文串的长度是偶数
// 跳出循环的时候恰好满足 s.charAt(left) != s.charAt(right)
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)){
left--;
right++;
}
//因为跳出循环时,s.charAt(left)!= s.charAt(right),即不包括此时的left和right,所以应该是[left+1,right-1],即(right-1)-(left+1)+1=right-left-1
//回文串的长度是right-left+1-2 = right - left - 1
return right - left - 1;
}
}
class Solution {
public String longestPalindrome(String s) {
if(s.length()<2) return s;
int n = s.length();
boolean[][] dp = new boolean[n][n];//dp[i][j]:字符串从i到j是否为回文
int max_len = 1;//最长回文长度至少是1,∵一个字符也是回文
int start=0;//最长回文起点
int end=0;//最长回文终点
for(int r=1;r<n;r++){
for(int l=0;l<r;l++){
if(s.charAt(l) == s.charAt(r) && (r-l<3 || dp[l+1][r-1])){
dp[l][r] = true;
if(r-l+1>max_len){
max_len = r-l+1;
start=l;
end = r;
}
}
}
}
return s.substring(start,end+1);
}
}
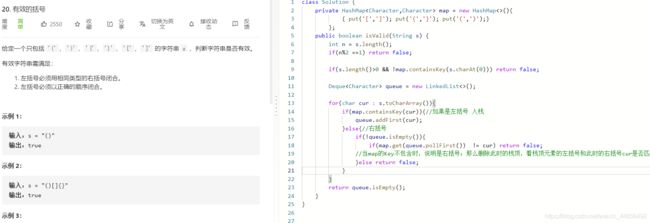
L20:有效括号
L43:字符串相乘
class Solution {
public String multiply(String num1, String num2) {
if(num1.equals("0") || num2.equals("0")) return "0";
String res = "0";
for(int i=num2.length()-1;i>=0;i--){
int carry = 0;
StringBuilder temp = new StringBuilder();//记录num2的当前i位上的数与nums1乘积的结果
//补0
for(int ii=0;ii<num2.length()-1-i;ii++){
temp.append(0);
}
int n2 = num2.charAt(i)-'0';//num2的当前i位上的数
//num2 的第 i 位数字 n2 与 num1 相乘
for(int j=num1.length()-1;j>=0 || carry!=0;j--){//∵存在j=-1(最低位前),但是进位carry上仍有数
int n1= j<0? 0 : num1.charAt(j)-'0';
int product = (carry+n1*n2)%10;//余数放到product
temp.append(product);
carry = (carry+n1*n2)/10;
}
res = addStrings(res,temp.reverse().toString());//将当前结果与新计算的结果求和作为新的结果
}
return res;
}
//对两个字符串数字进行相加,返回字符串形式的和
public String addStrings(String num1, String num2){
StringBuilder builder = new StringBuilder();
int carry=0;
for(int i=num1.length()-1,j=num2.length()-1;i>=0 || j>=0 || carry!=0;i--,j--){
int x = i<0? 0 : num1.charAt(i)-'0';
int y = j<0? 0 : num2.charAt(j)-'0';
int sum = (x+y+carry)%10;
builder.append(sum);
carry = (x+y+carry)/10;
}
return builder.reverse().toString();
}
}
10、二分查找
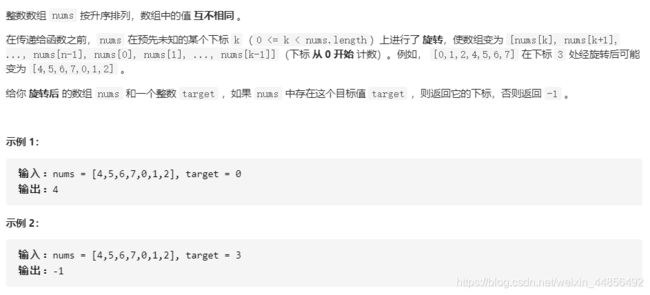
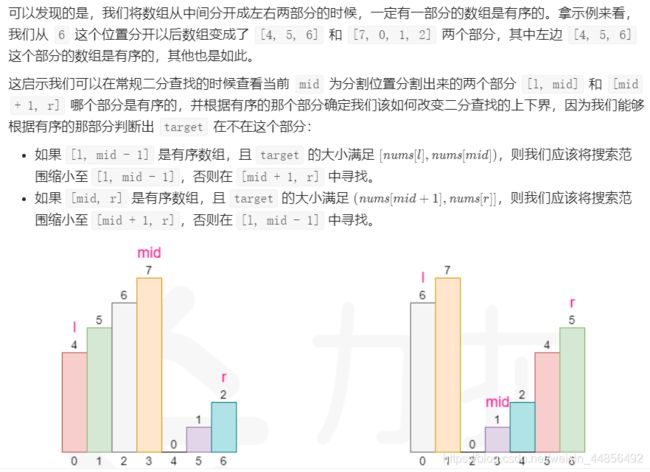
L33:搜索旋转排序数组
class Solution {
public int search(int[] arr, int target) {
int start = 0;
int end = arr.length-1;
int mid;
if(arr == null || arr.length == 0) return -1;
if(arr.length == 1) return target==arr[0]? 0: -1;
while(start <= end){
mid = start+(end-start)/2;
if(arr[mid] == target) return mid;
if(arr[mid]>= arr[start]){//情形1:左边有序
if(target >= arr[start] && target < arr[mid]){//情形1.1:target位于左边
end = mid-1;//左边右届缩小
}else{//情形1.2:target位于右边
start = mid +1;//右边左届缩小
}
}else{//情形2:右边有序
if(target> arr[mid] && target <= arr[end]){//情形2.1:target位于右边
start = mid+1;//右边左届缩小
}else{//情形2.2:target位于左边
end = mid-1;//左边右届缩小
}
}
}
return -1;
}
}
L34:在排序数组中查找元素的第一个和最后一个位置
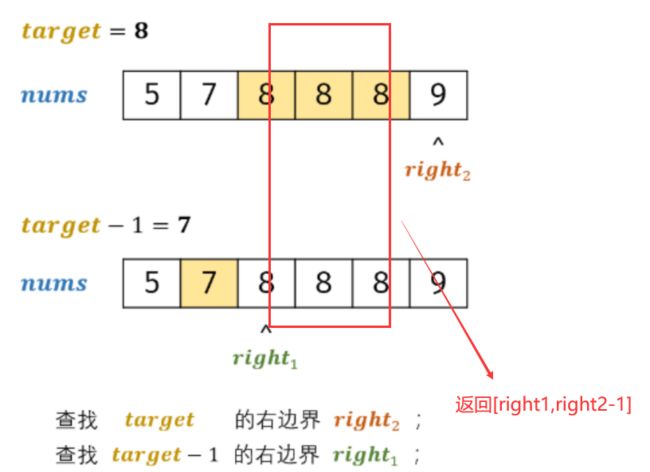
思路:
参考传送门,首先找到target-1的右边界,即target的起始第一个位置start,然后找到target的右边界,即target+1的起始位置xx,end=xx-1即target的最后一个位置,返回[start,end]
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length==0) return new int[]{-1,-1};
int start = helper(nums,target-1);//target第一个位置
int end = helper(nums,target)-1;//target最后一个位置
if(start>end) return new int[]{-1,-1};//说明没找到
return new int[]{start,end};
}
public int helper(int[] nums,int target){
int i=0;
int j=nums.length-1;
while(i<=j){
int mid = (i+j)>>1;
if(nums[mid]<=target){
i = mid+1;
}else{
j = mid-1;
}
}
return i;
}
}
11、BFS
L127:
L:139
class Solution {
int[] dx = {1,-1,0,0};//下,上,
int[] dy = {0,0,1,-1};//右,左
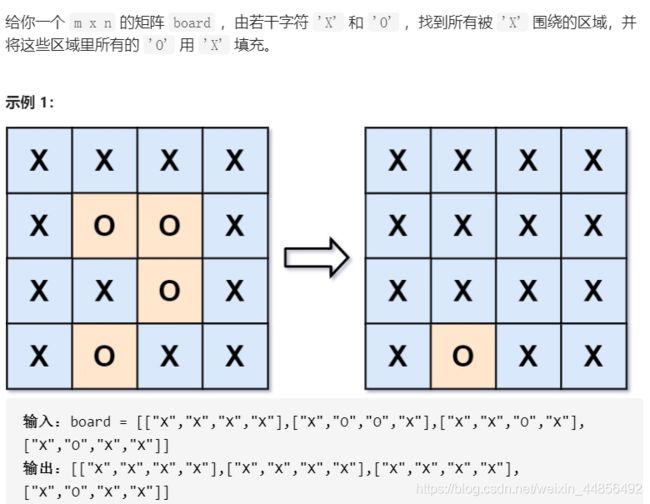
public void solve(char[][] board) {
int n = board.length;
int m = board[0].length;
if(n==0) return;
Queue<int[]> queue = new LinkedList<int[]>();
for(int i=0;i<n;i++){//列边界上的0
if(board[i][0]=='O'){
queue.offer(new int[]{i,0});
board[i][0]='A';
}
if(board[i][m-1]=='O'){
queue.offer(new int[]{i,m-1});
board[i][m-1]='A';
}
}
for(int j=0;j<m;j++){//行边界上的0
if(board[0][j]=='O'){
queue.offer(new int[]{0,j});
board[0][j]='A';
}
if(board[n-1][j]=='O'){
queue.offer(new int[]{n-1,j});
board[n-1][j]='A';
}
}
while(!queue.isEmpty()){//搜索每个边界上的0 的直接或间接相邻的0 标记位A
int[] tmp = queue.poll();
int x = tmp[0], y =tmp[1];
for(int i=0;i<4;i++){
int mx = x+dx[i], my = y+dy[i];
if(mx<0 || my<0 || mx>=n || my >=m || board[mx][my]!='O') continue;
queue.offer(new int[]{mx,my});
board[mx][my]='A';
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(board[i][j]=='A') board[i][j]='O';
else if (board[i][j] == 'O') board[i][j]='X';
}
}
}
}
L529:扫雷游戏
L:815
12、DFS&回溯
代码:
class Solution {
public int numIslands(char[][] grid) {
int count =0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]=='1'){
dfs(grid,i,j);
count++;
}
}
}
return count;
}
public void dfs(char[][] grid,int i,int j){
if(i<0 || j<0 || i>=grid.length|| j >=grid[0].length || grid[i][j]== '0') return;
grid[i][j]='0';//考虑到连续岛屿,即连续的1
dfs(grid,i+1,j);
dfs(grid,i,j+1);
dfs(grid,i,j-1);
dfs(grid,i-1,j);
}
}
L;685
L332:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int rob(TreeNode root) {
int[] res = dfs(root);
return Math.max(res[0],res[1]);
}
public int[] dfs(TreeNode node){
if(node==null) return new int[]{0,0};
// 由于需要后序遍历,所以先计算左右子结点,然后计算当前结点的状态值
int[] left = dfs(node.left);
int[] right = dfs(node.right);
int select = node.val+left[1]+right[1];//选择当前节点,则它的左右孩子都不能选
int NotSelect = Math.max(left[0],left[1])+Math.max(right[0],right[1]);
//不选该节点,它的左右孩子可以选,而且可以都选
return new int[]{select,NotSelect};
}
}
13、动态规划
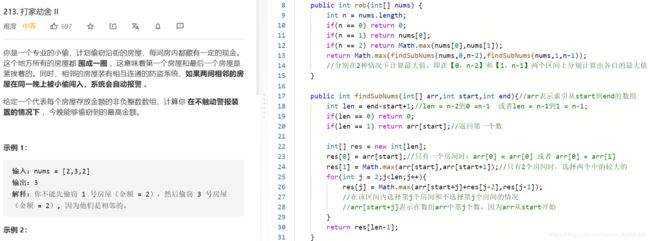
L213:打家劫舍||
- 和T198相比(首尾不相邻),只是多了选大小的语句
- 首尾相邻,结果只有两种情况;
1、选第一个,最后一个不选,那么在【0,n-2】区间进行T198的计算
2、不选第一个,最后一个选,那么在【1,n-1】区间进行T198的计算 - 然后针对1和2的结果,选择大的那个即可
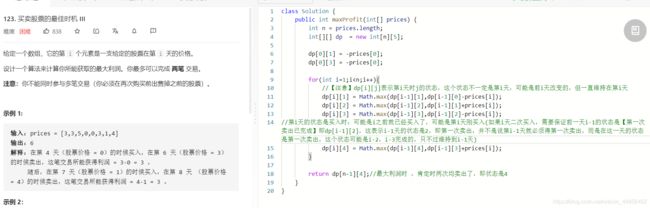
L123:
思路:动态规划
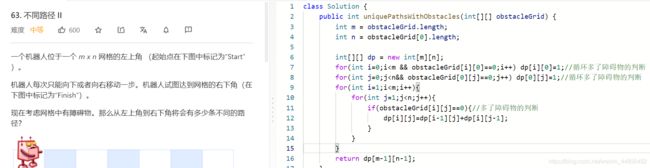
每次只能向右或向下走

优化:
cur[j] = cur[j-1] + cur[j]
未赋值之前右边的cur[j] 始终表示当前行第i行的上一行(i-1行)第j列的值,i
赋值之后左边的cur[j]表示当前行第i行第j列的值,cur[j-1] 表示当前行第i行第j-1列的值(cur[j-1] 在计算cur[j]之前就已经计算了,所以表示的是当前行而不是上一行 )
代码:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for(int i=0;i<m;i++){ dp[i][0] =1;}
for(int i=0;i<n;i++){ dp[0][i] =1;}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
dp[i][j] = dp[i][j-1] + dp[i-1][j];
}
}
return dp[m-1][n-1];
}
}
优化:
class Solution {
public int uniquePaths(int m, int n) {
int[] cur = new int[n];
Arrays.fill(cur,1);
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
cur[j] = cur[j] + cur[j-1];
//第一个cur[j]:当第i行j列的;第二个cur[j]:当前行的上一行和第j列的,即i-行,j列;
// cur[j-1]:当前行,j-1列,即i行j-1列
}
}
return cur[n-1];
}
}
L:361
L:1230
14、贪心
做出在当前看来是最好的选择 以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪心算法不要回溯。
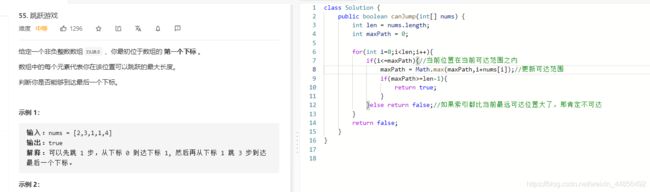
L:55
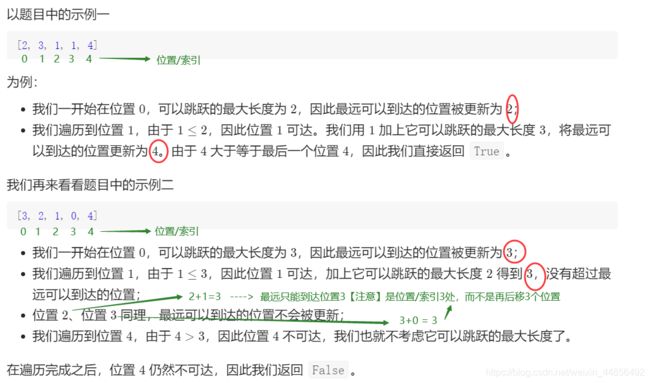
遍历数组每个数,每次更新当前可到达的最远位置,即索引,如果遇到最远位置(索引)超过数组末尾索引,说明可以达到;如果遍历完了,最远位置的记录值小于最后一个位置,则不可达。【注意】最远位置即数组的索引值,而不是说当前数后移多少个位置。

class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int count=0;//记录重叠区间的个数
if(intervals.length==0) return 0;
Arrays.sort(intervals,new Comparator<int[]>(){
public int compare(int[] o1,int[] o2){
return o1[1] - o2[1];
}
});
int rightEnd = intervals[0][1];//排序后首个区间的右端点
for(int i =1;i<intervals.length;i++){
if(intervals[i][0]>=rightEnd){//说明没有重叠,更新区间
rightEnd = intervals[i][1];
}else count++;
}
return count;
}
}
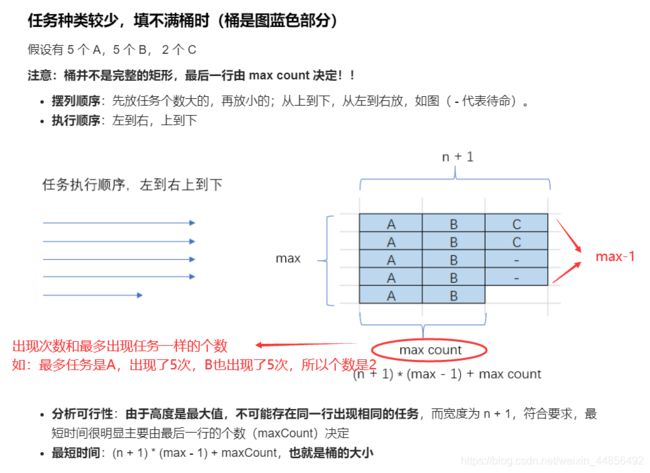
代码:
class Solution {
public int leastInterval(char[] tasks, int n) {
int[] buckets = new int[26];
//统计每个任务出现的次数
for(char task : tasks){
buckets[task - 'A'] +=1;
}
int max=0;//计算出现次数最多的任务
for(int i=0;i<26;i++){
max = Math.max(buckets[i],max);
}
//计算maxCount
int maxCount=0;//这个是0,而不是初始化为1
for(int i=0;i<26;i++){//因为遍历时把26个都遍历了,包括最大任务,所以最后maxCount必>=1;
if(buckets[i]==max){
maxCount++;
}
}
int res=0;
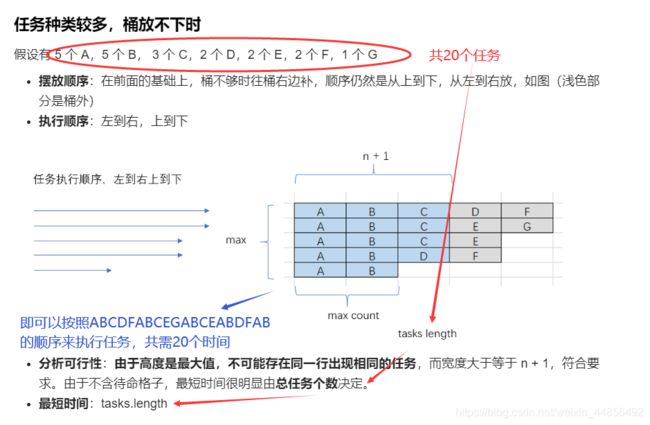
res = Math.max( (max-1)*(n+1)+maxCount, tasks.length);
return res;
}
}
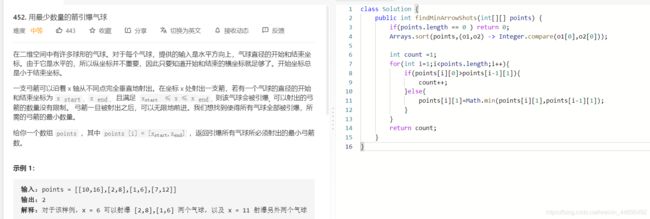
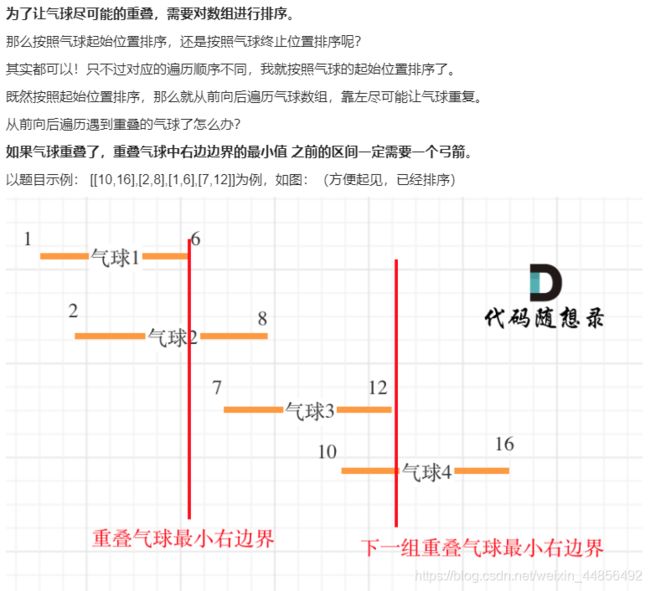
L:452
15、字典树
L820:单词的压缩编码
L208:
L648: