HDU 1067 GAP (BFS + HASH)
Gap
Time Limit: 20000/10000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 667 Accepted Submission(s): 366
Problem Description
Let's play a card game called Gap. You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.

Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.

At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.
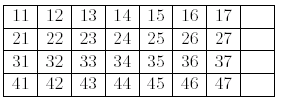
Your task is to find the minimum number of moves to reach the goal layout.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.

Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.

At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.

Your task is to find the minimum number of moves to reach the goal layout.
Input
The input starts with a line containing the number of initial layouts that follow.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Output
For each initial layout, produce a line with the minimum number of moves to reach the goal layout. Note that this number should not include the initial four moves of the cards of value 1. If there is no move sequence from the initial layout to the goal layout, produce "-1".
Sample Input
4 12 13 14 15 16 17 21 22 23 24 25 26 27 31 32 33 34 35 36 37 41 42 43 44 45 46 47 11 26 31 13 44 21 24 42 17 45 23 25 41 36 11 46 34 14 12 37 32 47 16 43 27 35 22 33 15 17 12 16 13 15 14 11 27 22 26 23 25 24 21 37 32 36 33 35 34 31 47 42 46 43 45 44 41 27 14 22 35 32 46 33 13 17 36 24 44 21 15 43 16 45 47 23 11 26 25 37 41 34 42 12 31
Sample Output
0 33 60 -1
学会了手写哈希,用的是AP哈希,此函数在前面的哈希函数对比那篇博文里有介绍,不解的是用来余的数稍微开的一点就MLE了,32G内存不至于这么快就用完吧。。。
#include <iostream>
#include <queue>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <string>
using namespace std;
const int MAX = 999991;
int G_MAP[][8] = {{0,0,0,0,0,0,0,0},
{11,12,13,14,15,16,17,0},
{21,22,23,24,25,26,27,0},
{31,32,33,34,35,36,37,0},
{41,42,43,44,45,46,47,0}};
int VIS[MAX];
int STEP;
unsigned int GOAL_HASH;
struct Node
{
int x,y;
};
struct State
{
int map[5][10];
Node pos[50],blank[4];
unsigned int hash;
int step;
void operator =(State const & r)
{
for(int i = 0;i < 5;i ++)
for(int j = 0;j < 10;j ++)
map[i][j] = r.map[i][j];
for(int i = 0;i < 50;i ++)
pos[i] = r.pos[i];
for(int i = 0;i < 4;i ++)
blank[i] = r.blank[i];
hash = r.hash;
step = r.step;
}
};
void APhash(State &);
int APhash(int (*)[8]);
int bfs(State &);
void debug(const State &);
int main(void)
{
int n;
GOAL_HASH = APhash(G_MAP);
scanf("%d",&n);
while(n --)
{
State first;
int count_blank = 0,count_num = 0;
memset(first.map,0,sizeof(first.map));
for(int i = 0;i < 50;i ++)
first.pos[i].x = first.pos[i].y = 0;
for(int i = 1;i <= 4;i ++)
for(int j = 1;j <= 7;j ++)
{
Node temp;
temp.x = i;
temp.y = j;
scanf("%d",&first.map[i][j]);
int temp_num = first.map[i][j];
if(temp_num % 10 == 1)
{
first.map[temp_num / 10][0] = temp_num;
first.map[i][j] = 0;
first.blank[count_blank ++] = temp;
}
else
{
first.pos[temp_num].x = i;
first.pos[temp_num].y = j;
}
}
first.step = 0;
printf("%d\n",bfs(first));
}
return 0;
}
void APhash(State & r)
{
unsigned hash = 0;
for(int i = 1;i <= 4;i ++)
for(int j = 0;j < 8;j ++)
if(r.map[i][j] & 1)
hash ^= (~((hash << 11) ^ r.map[i][j] ^ (hash >> 5)));
else
hash ^= ((hash << 7) ^ r.map[i][j] ^ (hash >> 3));
r.hash = (hash & 0x7fffffff) % MAX;
}
int APhash(int (* s)[8])
{
unsigned hash = 0;
for(int i = 1;i <= 4;i ++)
for(int j = 0;j < 8;j ++)
if(s[i][j] & 1)
hash ^= (~((hash << 11) ^ s[i][j] ^ (hash >> 5)));
else
hash ^= ((hash << 7) ^ s[i][j] ^ (hash >> 3));
return ((hash & 0x7fffffff) % MAX);
}
int bfs(State & r)
{
memset(VIS,0,sizeof(VIS));
queue<State> que;
que.push(r);
APhash(r);
if(r.hash == GOAL_HASH)
return r.step;
while(!que.empty())
{
State cur = que.front();
que.pop();
for(int i = 0;i < 4;i ++)
if(cur.blank[i].y >= 1 && cur.blank[i].y <= 7)
{
State next = cur;
int num = cur.map[cur.blank[i].x][cur.blank[i].y - 1] + 1;
if((num % 10 == 8) || (num == 1))
continue;
next.map[cur.pos[num].x][cur.pos[num].y] = 0;
next.map[cur.blank[i].x][cur.blank[i].y] = num;
APhash(next);
next.step ++;
if(VIS[next.hash] == 1)
continue;
if(next.hash == GOAL_HASH)
return next.step;
next.pos[num] = cur.blank[i];
next.blank[i] = cur.pos[num];
VIS[next.hash] = 1;
que.push(next);
}
}
return -1;
}
void debug(const State & r)
{
cout << endl;
printf("hash=%d\n",r.hash);
for(int i = 1;i <= 4;i ++)
{
for(int j = 0;j < 8;j ++)
printf("%d ",r.map[i][j]);
cout << endl;
}
cout << endl;
}