灰狼优化算法训练多层感知神经网络研究(Matlab代码实现)
个人主页:研学社的博客
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 参考文献
4 Matlab代码、数据、文章讲解
1 概述
本文首次采用最近提出的灰狼优化器(GWO)来训练多层感知器(MLP)。利用8个标准数据集(包括5个分类数据集和3个函数近似数据集)对所提方法的性能进行基准测试。为了验证,将结果与一些最著名的进化训练器进行了比较:粒子群优化(PSO),遗传算法(GA),蚁群优化(ACO),进化策略(ES)和基于群体的增量学习(PBIL)。统计结果证明,GWO算法在改进局部最优避免方面能够提供非常有竞争力的结果。结果还表明,拟议培训师的分类和近似准确率很高。
神经网络(NN)是计算智能领域最伟大的发明之一。它们模仿人脑的神经元,主要解决分类问题。NN的基本概念于1943年首次提出[1]。文献中提出了不同类型的神经网络:前馈网络 [2]、Kohonen 自组织网络 [3]、径向基函数 (RBF) 网络 [4]、递归神经网络 [5] 和尖峰神经网络 [6]。在前馈神经网络 (FNN) 中,信息在整个网络中沿一个方向级联。然而,顾名思义,递归神经网络在两个方向上共享神经元之间的信息。最后,尖峰神经网络激活具有尖峰的神经元。
尽管 NN 存在差异,但它们在学习中很常见。学习是指 NN 从经验中学习的能力。与生物神经元类似,人工神经网络(ANN)已经配备了适应一组给定输入的机制。这里有两种常见的学习类型: 监督 .[7, 8] 和无监督 [9, 10]。在前一种情况下,NN 会从外部来源(主管)获得反馈。然而,在无监督学习中,神经网络在没有任何额外外部反馈的情况下适应输入(学习)。
一般来说,为 NN 提供学习的方法称为培训师。培训师负责训练 NN,以针对新的给定输入集实现最高性能。在监督学习中,训练方法首先为 NN 提供一组称为训练样本的样本。然后,训练师在每个训练步骤中修改 NN 的结构参数,以提高性能。训练阶段完成后,将省略培训师,NN 即可使用。培训师可以被认为是任何 NN 中最重要的组成部分。
文献中有两种类型的学习方法:确定性和随机性。反向传播(BP)[11]和基于梯度的方法被认为是确定性方法。在此类技术中,如果训练样本保持一致,则训练阶段会产生相同的性能。该组中的培训师大多是数学优化技术,旨在找到最大性能(最小误差)。相比之下,随机训练器利用随机优化技术来最大化 NN 的性能。
确定性训练器的优点是:简单和快速。确定性训练算法通常从解决方案开始,并引导其达到最佳状态。收敛速度非常快,但得到的解的质量在很大程度上取决于初始解。此外,局部最优诱捕的可能性很高。局部最优是指搜索空间中的次优解,可能会被错误地假定为全局最优。这里的挑战是训练器需要重新启动未知的运行次数,使用不同的初始解决方案来找到全局最佳。
相比之下,随机训练器从随机解决方案开始训练过程并对其进行演变(它们)。随机性是随机训练器的重要组成部分,适用于初始解决方案和训练过程中解决方案改进的方法。这些方法的优点是高度局部最优避免,但它们大多比确定性方法慢得多[12],[13]。文献表明,随机训练方法近年来受到广泛关注,这是由于高度的局部最优回避。
随机训练算法可分为两组:单解和基于多解的算法[14]。在前一类中,培训师使用单个随机构造的 NN 开始训练,并迭代地发展它,直到满足最终标准。基于单一解决方案的训练器的例子是模拟退火(SA)[15,16]和爬山[17,18]。与基于单解的方法相比,基于多解的算法通过一组随机创建的 NN 启动训练过程,并将它们相互发展,直到满足最终标准。文献表明,具有多种解决方案的随机算法提供了更高的解决局部最优停滞的能力[19]。
文献中一些最受欢迎的多解决方案训练器是:遗传算法(GA)[19,20],粒子群优化(PSO)[21,22],蚁群优化(ACO)[23,24],人工蜂群(ABC)[25,26]和差分进化(DE)[27,28].最近的进化训练算法是:混合中心力优化和粒子群优化(CFO-PSO)[29],社交蜘蛛优化算法(SSO)[30],化学反应优化(CRO)[31]带电系统搜索(CSS)[32],入侵杂草优化(IWO)[33]和基于教学的优化(TLBO)训练器[34].之所以将这种优化技术用作训练算法,是因为它们在近似全局最优方面的高性能。这也促使我尝试研究我最近提出的称为灰狼优化器(GWO)[14]的算法在训练FNN方面的效率。
详细文章见第4部分。
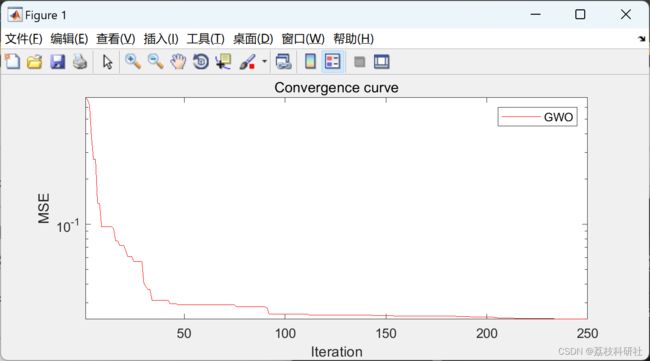
2 运行结果
部分代码:
% Srat traning using GWO
[Best_MSE,Best_NN,cg_curve]=GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
% Draw the convergence curve
figure('Position',[500 500 660 290])
semilogy(cg_curve,'Color','r')
hold on
title('Convergence curve')
xlabel('Iteration');
ylabel('MSE');
axis tight
grid off
box on
legend('GWO')
% Calculate the classification rate
% load the dataset and normalization
load iris.txt
x=sortrows(iris,2);
%I2=x(1:150,1:4);
H2=x(1:150,1);
H3=x(1:150,2);
H4=x(1:150,3);
H5=x(1:150,4);
T=x(1:150,5);
%I=(I2-0.1)./(7.9-0.1)
H2=H2';
[xf,PS] = mapminmax(H2);
I2(:,1)=xf;
H3=H3';
[xf,PS2] = mapminmax(H3);
I2(:,2)=xf;
H4=H4';
[xf,PS3] = mapminmax(H4);
I2(:,3)=xf;
H5=H5';
[xf,PS4] = mapminmax(H5);
I2(:,4)=xf;
Thelp=T;
T=T';
[yf,PS5]= mapminmax(T);
T=yf;
T=T';
Rrate=0;
% Load the obtained optimal values for weights and biases
W=Best_NN(1:63);
B=Best_NN(64:75);
for pp=1:150
actualvalue=My_FNN(4,9,3,W,B,I2(pp,1),I2(pp,2), I2(pp,3),I2(pp,4));
if(T(pp)==-1)
if (actualvalue(1)>=0.95 && actualvalue(2)<0.05 && actualvalue(3)<0.05)
Rrate=Rrate+1;
end
end
if(T(pp)==0)
if (actualvalue(1)<0.05 && actualvalue(2)>=0.95 && actualvalue(3)<0.05)
Rrate=Rrate+1;
end
end
if(T(pp)==1)
if (actualvalue(1)<0.05 && actualvalue(2)<0.05 && actualvalue(3)>=0.95)
Rrate=Rrate+1;
end
end
end
Classification_rate=(Rrate/150)*100
3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]S. Mirjalili,How effective is the Grey Wolf optimizer in training multi-layer perceptrons Applied Intelligece, in press, 2015,