- 机器学习数据预处理阶段为什么需要——归一化处理
参考:https://www.cnblogs.com/bjwu/p/8977141.html通常,在DataScience中,预处理数据有一个很关键的步骤就是数据的标准化。这里主要引用sklearn文档中的一些东西来说明,主要把各个标准化方法的应用场景以及优缺点总结概括,以来充当笔记。提升模型精度在机器学习算法的目标函数(例如SVM的RBF内核或线性模型的l1和l2正则化),许多学习算法中目标函数
- Vue 3 组合式 API 中的组件生命周期函数详解
码力无边-OEC
Vuevue.js前端javascript前端框架web
Vue3组合式API中的组件生命周期函数详解Vue3引入了组合式API(CompositionAPI),相比于选项式API(OptionsAPI),它更加灵活且易于复用。在组件的开发中,生命周期函数是必不可少的一部分,用于在特定的阶段执行逻辑操作。本文将详细讲解Vue3组合式API的生命周期函数及其相关知识点,并通过语法糖实现相关示例。什么是生命周期函数?Vue组件从创建到销毁的过程中,会经历一系
- 【C++11】哈希表与无序容器:从概念到应用
卜及中
C++初阶知识C++进阶哈希算法c++算法
文章目录一、前言二、哈希表(HashTable)1.基本概念2.哈希函数3.冲突解决方法链地址法(SeparateChaining)开放寻址法(OpenAddressing)4.性能分析5.动态扩容6.应用场景7.优缺点二.无序容器的介绍1.unordered_set2.unordered_map3.unordered_multiset4.unordered_multimap5.总结三.无序容器与
- “重复”定义函数的睿智(Python/与ai助手“智普清言”深度交流)
梦幻精灵_cq
笔记学习
镜像双胞谬重复,定制便捷巧活工。 笔记模板由python脚本于2025-07-1612:16:30创建,本篇笔记适合至少通晓一门语言,熟悉基本编程范式的coder翻阅。学习的细节是欢悦的历程 博客的核心价值:在于输出思考与经验,而不仅仅是知识的简单复述。Python官网: 这里,才python前沿。英文原版,原汁原味,才是寻根溯源的正统。地址:https://www.python.org/F
- 详解C语言函数——一篇看完彻底学会使用自定义函数
秋刀鱼的滋味@
C语言语法详解c语言开发语言c++
目录1.函数前言1.1函数的概念:1.2为什么要使用函数:2.标准库函数2.1什么是标准库:2.2库函数有哪些:3.自定义函数3.1函数的定义:3.2函数的声明:3.4函数的调用:4.实参和形参4.1实参:4.2形参:4.3实参和形参的关系5.数组传参6.return语句6.1return语句作用:6.2常见的return问题:7.嵌套函数和链式访问7.1嵌套函数:7.2链式访问(例-printf
- “疫战”之下,“枕戈”以待⑪又见黄码
潭客的语文生活
“疫战”之下,“枕戈”以待⑪又见黄码“你健康码有变吗?”阿易的微信好友里再次出现了这个已经让他淡忘的字眼。“没有呀,还是绿码。怎么啦!”阿易依旧充满疑惑。“恭喜,我变黄了。”“什么?!是什么时候变的?”“下午三点左右,社区通知。我就路过而已呀。”她说的路过指的是:六一环岛+古田路+宜发大厦+劳动大厦,还有福新路与长乐路交叉口,这几个地方路过就有变黄码可能。阿易一身冷汗,他中午回来的路线里就有六一路
- 2023-04-03
向日葵积极向上
每日一省导师班复训结束了,这一次断断续续的听课,听的不是很好,不过,还是有收获的,今天的实操流程有很大的启发。今天老公又说,你学了这么久有用的不嘛?问题解决了没?怎么还是这个样子呢?他爱怎么怎么的,我好解脱……听到他这样说,我心里就在想,这货就那样,固执又不学习,他自己也没招,把希望寄托在我身上,希望我去解决目前的问题(一直以来都这样,只要有事就是我的事)。我说:我们养了十几年的娃,十几年的教育结
- python双引号打不出来_在python 3中使用单引号和双引号时出错 - python
weixin_39897749
python双引号打不出来
使用os.system()函数时,我在python中遇到了EOL错误。以下是代码行生成错误:os.system("catsubdomains.txt|cut-d'"'-f1")基本上,我试图使用分号[“]修改输出字符串(双引号)参考方案如果需要在带"的字符串中编写",则可以将其写为\""catsubdomains.txt|cut-d'\"'-f1"在PythonCloudFunction中使用错误
- 2023-07-16
幸福的玲宝宝
感恩7/15感恩今天发工资啦,好开心,钱宝宝进账!感恩老公孩子和我一起填报中考志愿一家人其乐融融,欢声笑语,看到老公对孩子的重视,好开心!感恩自己勇敢上台分享自己的真实发生,看见了自己的模式,情绪化,感恩龙溪老师的点评!感恩庆文中午再次请我吃饭,谢谢庆文!感恩姐妹们夸我勇敢和进步,一群人,走的更远!感恩7/14感恩今天自己一个人面对客户,谈了好几个年卡,事上勤奋,结果随缘,真好!感恩一位交警帮我复
- 阳明三变
凤凰鸟
共读阳明《传习录》第28天今天共读陆澄录三十八——四十二(64—65页)今天读的这几节都比较短,也没有想到什么。最后王荣平老师跟我们分享他们在旺苍共读的情况。王胜男老师说她感触最深的是:参加共读的老师都很卷,勇猛精进,王昌侠老师晚上十二点多睡,早晨四点多起来去教室参加共读,还有老师晚上在教室码字写体会很晚。王荣平老师也提到一些老师早晨早早到教室参加自己的共读,都很拼的。真不知道这一群人的动力从哪来
- 反反复复的小明
康康的视野
问题生教育总是不断重复着过去的故事,班主任总是在与学生斗智斗勇中渡过一个又一个的工作日。今天下午本来是我们市里初二语文岗培的时间,由于抗疫,岗培改为钉钉平台上看老师的直播讲座。我开着手机,戴着耳机,边听课边改周记。第二节课上课,生物老师带了四个我班上学生来找我,其中两个是因到图书馆借书而迟到,两个上课还在打架。于是只好手机里放着视频直播课,自己处理这几个孩子违纪的事情。先逐一了解情况,小明和阿泽借
- 惩罚不是体罚
han满天星
前段时间教育部颁发了《中小学教育惩戒规则(试行)》,很多教师都松了一口气:整天面对批评不得,招不得的学生,时刻盯着老师的一举一动,随时准备上访的家长,真是如履薄冰,现在终于有法可依了。真正阅读了《中小学教育惩戒规则(试行)》之后,才发现,《规则》虽然详细规定了能够实施惩戒的具体情况,但同时又对教师严厉禁止的行为,做出了非常细化的规定。《规则》既充分保证了教师的权利,也充分保证了学生不受到体罚以及变
- 从 0 到 1 搞定nvidia 独显推流:硬件视频编码环境安装完整学习笔记
lxmyzzs
图像算法之音视频编解码音视频学习笔记
笔记用于安装和配置一套完整的媒体处理工具链,包括NVIDIA编码头文件、带CUDA加速的FFmpeg以及ZLMediaKit流媒体服务框架,适用于需要进行视频编解码、流媒体推流/拉流等场景的开发与部署。标题核心组件及版本说明nv-codec-headers来源:Gitee仓库jario-jin/nv-codec-headers版本:n11.1.5.0(对应NVIDIAVideoCodecSDK接口
- 【C++11】lambda表达式 | 函数包装器
_宁清
C++c++lambda函数包装器bindfunctionlambda表达式
文章目录一、lambda表达式1.为什么需要lambda表达式2.lambda的定义3.lambda的语法捕捉列表4.函数对象和lambda表达式的底层原理二、函数包装器1.function包装器2.bind包装器用bind包装器绑定固定参数用bind包装器调整传参顺序无意义的绑定3.bind包装器的意义一、lambda表达式1.为什么需要lambda表达式在C++98中,如果想要对一个数据集合中
- 学习笔记56-(已解决)pip指令下载超时Read timed out错误
李卓璐
报错整理pip
(已解决)pip指令下载超时Readtimedout错误下了一上午卡到自闭然后查了很多帖子,最后更换国内安装源和设置超时时间可以解决。在pip3installXXX命令的后面加上–default-timeout=100-ihttps://pypi.tuna.tsinghua.edu.cn/simple
- 商汤科技视觉算法面试30问全景精解
商汤科技视觉算法面试30问全景精解——AI赋能×智能视觉×产业创新:商汤科技视觉算法面试核心考点全览前言商汤科技(SenseTime)作为全球领先的人工智能平台公司,专注于计算机视觉、深度学习和智慧城市、智能汽车、智能医疗等领域,推动人脸识别、目标检测、视频分析、自动驾驶等前沿技术的产业化落地。商汤视觉算法岗位面试不仅考察候选人对视觉基础理论的扎实掌握,更关注其在大规模安防、自动驾驶、智慧医疗等复
- Go语言面试宝典:50道必会题目与精解_golang面试必问50个问题
2401_86436851
golang面试开发语言
1.指针与引用2.并发编程3.切片与数组4.接口5.垃圾回收6.错误处理7.包管理8.Map9.Defer语句10.类型断言11.并发同步12.接口实现13.错误跟踪14.并发性能15.内存管理16.编译和运行17.泛型18.网络编程19.测试20.代码组织21.Goroutine泄漏22.闭包23.指针与性能24.错误封装25.接口与空接口26.并发错误27.切片操作28.字符串处理29.环境变
- 5.Kotlin协程
热爱Android的人
kotlin
文章目录1.协程的基本用法1.1先添加依赖库1.2开启一个协程GlobalScope.launch函数delay()函数Thread.sleep()函数runBlocking函数1.3创建多个协程launch函数suspend关键字coroutineScope函数2.更多的作用域构建器async函数withContext()函数线程参数3.使用协程简化回调的写法suspendCoroutine函数
- R语言使用glmnet包拟合lasso-cox回归模型(包含生存时间和结果标签)、使用lasso-cox模型进行特征筛选、使用sapply函数对特征数据进行标准化z-score
statistics.insight
R语言入门课机器学习人工智能r语言数据挖掘数据分析
R语言使用glmnet包拟合lasso-cox回归模型(包含生存时间和结果标签)、使用lasso-cox模型进行特征筛选、使用sapply函数对特征数据进行标准化z-score目录R语言使用glmnet包拟合lasso-cox回归模型(包含生存时间和结果标签)、使用lasso-cox模型进行特征筛选、使用sapply函数对特征数据进行标准化z-score分类模型(classification)决策
- Python 线程优先队列 PriorityQueue - Python零基础入门教程
猿说编程
目录一.Python线程队列Queue分类二.Python线程优先队列PriorityQueue简介三.Python线程优先队列PriorityQueue函数介绍四.Python线程优先队列PriorityQueue使用五.猜你喜欢零基础Python学习路线推荐:Python学习目录>>Python基础入门在线程队列Queue/线程队列LifoQueue文章中分别介绍了先进先出队列Queue和先进
- 使用Debug-View Kotlin,提升你的Android调试体验!
侯深业Dorian
使用Debug-ViewKotlin,提升你的Android调试体验!去发现同类优质开源项目:https://gitcode.com/1、项目介绍Debug-ViewKotlin是一个专为Android开发者设计的高效、直观的浮层调试控制台。它会在应用界面的最上方提供实时的性能指标和日志信息,包括但不限于内存占用、帧率(FPS)、启动时间和各种自定义的日志数据。只需简单集成,就能让开发和测试过程变
- 生个孩子吧!
道路yu梦想
图片发自App春节前几天我家宝宝出生,到今天刚好过去43天,昨天是妻子术后第一次复查的时间。我在家照顾宝宝,妻子一个人去医院。经过妻子的一个月子期,照顾宝宝对我来说并非难事,只是妻子的复查结果并不遂愿,还需要进一步恢复和定期复查。今天又带宝宝去妇幼保健站做听力复筛,刚出生在医院做筛查时一只耳朵没有通过,今天都通过了。前两天去社区卫生服务中心打了疫苗、建了档案,接下来还要去好多次,打疫苗、定期填表…
- 深度强化学习 | 图文详细推导深度确定性策略梯度DDPG算法
Mr.Winter`
机器人人工智能数据挖掘深度学习神经网络强化学习具身智能
目录0专栏介绍1演员-评论家架构1.1Critic网络优化1.2Actor网络优化2深度确定性策略梯度算法0专栏介绍本专栏以贝尔曼最优方程等数学原理为根基,结合PyTorch框架逐层拆解DRL的核心算法(如DQN、PPO、SAC)逻辑。针对机器人运动规划场景,深入探讨如何将DRL与路径规划、动态避障等任务结合,包含仿真环境搭建、状态空间设计、奖励函数工程化调优等技术细节,旨在帮助读者掌握深度强化学
- 【Python练习】056. 编写一个函数,实现简单的CSV文件解析器
视睿
从零开始学习机器人python前端服务器
056.编写一个函数,实现简单的CSV文件解析器056.编写一个函数,实现简单的CSV文件解析器示例代码示例CSV文件内容示例运行代码说明扩展功能支持自定义分隔符的示例注意事项实现CSV文件解析的方法使用标准库csv模块解析使用pandas库解析手动实现基础解析器处理复杂CSV格式性能优化建议056.编写一个函数,实现简单的CSV文件解析器以下是一个简单的Python函数,用于解析CSV文件。这个
- 曲中人
武汉小明同学
以为自己够洒脱却逃不开这命运的曲折有时觉得很脆弱忽然发现没人可以诉说心早已不愿漂泊却注定没了奢求的资格多少深夜独自难过反复重播着这首歌初闻不知曲中意再听已是曲中人谁是谁非爱与恨满身的伤痕昔日浪漫的回忆如今早已变陌生只怨老天太弄人坎坷的红尘
- gpt面试题
任小栗
#面试题gptvue.js前端
vue面试题一、响应式系统相关❓1.Vue3的响应式系统是如何实现的?和Vue2有何本质区别?答案:Vue3使用Proxy实现响应式(位于@vue/reactivity模块),替代Vue2的Object.defineProperty。核心机制如下:使用targetMap:WeakMap存储依赖关系利用track()和trigger()方法实现依赖收集与派发更新effect()包装副作用函数,自动收
- c++读取文件中图像信息并用opencv展示
送分童子笑嘻嘻
#include#include#include#include#include#include#include//usingnamespacestd;usingnamespacecv;//字符串分割函数,std::vectorsplit(std::stringstr,std::stringpattern){std::string::size_typepos;std::vectorresult;s
- 易效能一阶 G188期的90天践行正式开始
任旻
G188期是我参加第二次复训的班级,第一次参加的是G151,2017年的三八节在成都开启了真正的易效能系统的学习和践行。第一次复训是G169重庆班,这次也是重庆班,与前两次有很多不同的地方:1.强大的教练团队支持,有每年读书300本的教练带班,有全球工具使用最牛的教练,有易效能系统的学习部部长带教练团队的教练等等。全班来了二三十位教练。2.课程内容的升级,两天全是满满干活,get到不少的新知识,在
- 我的2022上半年总结
随心墨痕
七月已过一周,回顾上半年,今天对自己上半年做一个小的总结。2022年,对我来说是非常特别的一年,无论是读书学习,还是工作生活,都发生了很多变化,而且都是积极的变化。接下来从几个方面对自己做个复盘总结。1、读书今年计划共读书籍有13本,《让时间陪你慢慢变富》、《原则1、2》、《文明、现代化、价值投资与中国》、《穷查理宝典》、《滚雪球》、《聪明的投资者》、《价值投资的秘密》、《思考,快与慢》、《股市长
- 桃花流水鳜鱼肥
网中的水滴
渔歌子·西塞山前白鹭飞唐张志和西塞山前白鹭飞,桃花流水鳜鱼肥。青箬笠,绿蓑衣,斜风细雨不须归。图片发自App庄子说:“独与天地精神往来”,人只有在独处之时,方能拨开迷雾,心灵游于物外,与天地精神往来,看清生命的真相。独处,是一种高远的人生境界。苏东坡写过一首词:夜饮东坡醒复醉,归来仿佛三更。家童鼻息已雷鸣,敲门都不应,倚杖听江声。长恨此身非我有,何时忘却营营。夜阑风静毂纹平,小舟从此逝,江海寄余生
- JAVA基础
灵静志远
位运算加载Date字符串池覆盖
一、类的初始化顺序
1 (静态变量,静态代码块)-->(变量,初始化块)--> 构造器
同一括号里的,根据它们在程序中的顺序来决定。上面所述是同一类中。如果是继承的情况,那就在父类到子类交替初始化。
二、String
1 String a = "abc";
JAVA虚拟机首先在字符串池中查找是否已经存在了值为"abc"的对象,根
- keepalived实现redis主从高可用
bylijinnan
redis
方案说明
两台机器(称为A和B),以统一的VIP对外提供服务
1.正常情况下,A和B都启动,B会把A的数据同步过来(B is slave of A)
2.当A挂了后,VIP漂移到B;B的keepalived 通知redis 执行:slaveof no one,由B提供服务
3.当A起来后,VIP不切换,仍在B上面;而A的keepalived 通知redis 执行slaveof B,开始
- java文件操作大全
0624chenhong
java
最近在博客园看到一篇比较全面的文件操作文章,转过来留着。
http://www.cnblogs.com/zhuocheng/archive/2011/12/12/2285290.html
转自http://blog.sina.com.cn/s/blog_4a9f789a0100ik3p.html
一.获得控制台用户输入的信息
&nbs
- android学习任务
不懂事的小屁孩
工作
任务
完成情况 搞清楚带箭头的pupupwindows和不带的使用 已完成 熟练使用pupupwindows和alertdialog,并搞清楚两者的区别 已完成 熟练使用android的线程handler,并敲示例代码 进行中 了解游戏2048的流程,并完成其代码工作 进行中-差几个actionbar 研究一下android的动画效果,写一个实例 已完成 复习fragem
- zoom.js
换个号韩国红果果
oom
它的基于bootstrap 的
https://raw.github.com/twbs/bootstrap/master/js/transition.js transition.js模块引用顺序
<link rel="stylesheet" href="style/zoom.css">
<script src=&q
- 详解Oracle云操作系统Solaris 11.2
蓝儿唯美
Solaris
当Oracle发布Solaris 11时,它将自己的操作系统称为第一个面向云的操作系统。Oracle在发布Solaris 11.2时继续它以云为中心的基调。但是,这些说法没有告诉我们为什么Solaris是配得上云的。幸好,我们不需要等太久。Solaris11.2有4个重要的技术可以在一个有效的云实现中发挥重要作用:OpenStack、内核域、统一存档(UA)和弹性虚拟交换(EVS)。
- spring学习——springmvc(一)
a-john
springMVC
Spring MVC基于模型-视图-控制器(Model-View-Controller,MVC)实现,能够帮助我们构建像Spring框架那样灵活和松耦合的Web应用程序。
1,跟踪Spring MVC的请求
请求的第一站是Spring的DispatcherServlet。与大多数基于Java的Web框架一样,Spring MVC所有的请求都会通过一个前端控制器Servlet。前
- hdu4342 History repeat itself-------多校联合五
aijuans
数论
水题就不多说什么了。
#include<iostream>#include<cstdlib>#include<stdio.h>#define ll __int64using namespace std;int main(){ int t; ll n; scanf("%d",&t); while(t--)
- EJB和javabean的区别
asia007
beanejb
EJB不是一般的JavaBean,EJB是企业级JavaBean,EJB一共分为3种,实体Bean,消息Bean,会话Bean,书写EJB是需要遵循一定的规范的,具体规范你可以参考相关的资料.另外,要运行EJB,你需要相应的EJB容器,比如Weblogic,Jboss等,而JavaBean不需要,只需要安装Tomcat就可以了
1.EJB用于服务端应用开发, 而JavaBeans
- Struts的action和Result总结
百合不是茶
strutsAction配置Result配置
一:Action的配置详解:
下面是一个Struts中一个空的Struts.xml的配置文件
<?xml version="1.0" encoding="UTF-8" ?>
<!DOCTYPE struts PUBLIC
&quo
- 如何带好自已的团队
bijian1013
项目管理团队管理团队
在网上看到博客"
怎么才能让团队成员好好干活"的评论,觉得写的比较好。 原文如下: 我做团队管理有几年了吧,我和你分享一下我认为带好团队的几点:
1.诚信
对团队内成员,无论是技术研究、交流、问题探讨,要尽可能的保持一种诚信的态度,用心去做好,你的团队会感觉得到。 2.努力提
- Java代码混淆工具
sunjing
ProGuard
Open Source Obfuscators
ProGuard
http://java-source.net/open-source/obfuscators/proguardProGuard is a free Java class file shrinker and obfuscator. It can detect and remove unused classes, fields, m
- 【Redis三】基于Redis sentinel的自动failover主从复制
bit1129
redis
在第二篇中使用2.8.17搭建了主从复制,但是它存在Master单点问题,为了解决这个问题,Redis从2.6开始引入sentinel,用于监控和管理Redis的主从复制环境,进行自动failover,即Master挂了后,sentinel自动从从服务器选出一个Master使主从复制集群仍然可以工作,如果Master醒来再次加入集群,只能以从服务器的形式工作。
什么是Sentine
- 使用代理实现Hibernate Dao层自动事务
白糖_
DAOspringAOP框架Hibernate
都说spring利用AOP实现自动事务处理机制非常好,但在只有hibernate这个框架情况下,我们开启session、管理事务就往往很麻烦。
public void save(Object obj){
Session session = this.getSession();
Transaction tran = session.beginTransaction();
try
- maven3实战读书笔记
braveCS
maven3
Maven简介
是什么?
Is a software project management and comprehension tool.项目管理工具
是基于POM概念(工程对象模型)
[设计重复、编码重复、文档重复、构建重复,maven最大化消除了构建的重复]
[与XP:简单、交流与反馈;测试驱动开发、十分钟构建、持续集成、富有信息的工作区]
功能:
- 编程之美-子数组的最大乘积
bylijinnan
编程之美
public class MaxProduct {
/**
* 编程之美 子数组的最大乘积
* 题目: 给定一个长度为N的整数数组,只允许使用乘法,不能用除法,计算任意N-1个数的组合中乘积中最大的一组,并写出算法的时间复杂度。
* 以下程序对应书上两种方法,求得“乘积中最大的一组”的乘积——都是有溢出的可能的。
* 但按题目的意思,是要求得这个子数组,而不
- 读书笔记-2
chengxuyuancsdn
读书笔记
1、反射
2、oracle年-月-日 时-分-秒
3、oracle创建有参、无参函数
4、oracle行转列
5、Struts2拦截器
6、Filter过滤器(web.xml)
1、反射
(1)检查类的结构
在java.lang.reflect包里有3个类Field,Method,Constructor分别用于描述类的域、方法和构造器。
2、oracle年月日时分秒
s
- [求学与房地产]慎重选择IT培训学校
comsci
it
关于培训学校的教学和教师的问题,我们就不讨论了,我主要关心的是这个问题
培训学校的教学楼和宿舍的环境和稳定性问题
我们大家都知道,房子是一个比较昂贵的东西,特别是那种能够当教室的房子...
&nb
- RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系
daizj
oraclermanfilespersetPARALLELISM
RMAN配置中通道(CHANNEL)相关参数 PARALLELISM 、FILESPERSET的关系 转
PARALLELISM ---
我们还可以通过parallelism参数来指定同时"自动"创建多少个通道:
RMAN > configure device type disk parallelism 3 ;
表示启动三个通道,可以加快备份恢复的速度。
- 简单排序:冒泡排序
dieslrae
冒泡排序
public void bubbleSort(int[] array){
for(int i=1;i<array.length;i++){
for(int k=0;k<array.length-i;k++){
if(array[k] > array[k+1]){
- 初二上学期难记单词三
dcj3sjt126com
sciet
concert 音乐会
tonight 今晚
famous 有名的;著名的
song 歌曲
thousand 千
accident 事故;灾难
careless 粗心的,大意的
break 折断;断裂;破碎
heart 心(脏)
happen 偶尔发生,碰巧
tourist 旅游者;观光者
science (自然)科学
marry 结婚
subject 题目;
- I.安装Memcahce 1. 安装依赖包libevent Memcache需要安装libevent,所以安装前可能需要执行 Shell代码 收藏代码
dcj3sjt126com
redis
wget http://download.redis.io/redis-stable.tar.gz
tar xvzf redis-stable.tar.gz
cd redis-stable
make
前面3步应该没有问题,主要的问题是执行make的时候,出现了异常。
异常一:
make[2]: cc: Command not found
异常原因:没有安装g
- 并发容器
shuizhaosi888
并发容器
通过并发容器来改善同步容器的性能,同步容器将所有对容器状态的访问都串行化,来实现线程安全,这种方式严重降低并发性,当多个线程访问时,吞吐量严重降低。
并发容器ConcurrentHashMap
替代同步基于散列的Map,通过Lock控制。
&nb
- Spring Security(12)——Remember-Me功能
234390216
Spring SecurityRemember Me记住我
Remember-Me功能
目录
1.1 概述
1.2 基于简单加密token的方法
1.3 基于持久化token的方法
1.4 Remember-Me相关接口和实现
- 位运算
焦志广
位运算
一、位运算符C语言提供了六种位运算符:
& 按位与
| 按位或
^ 按位异或
~ 取反
<< 左移
>> 右移
1. 按位与运算 按位与运算符"&"是双目运算符。其功能是参与运算的两数各对应的二进位相与。只有对应的两个二进位均为1时,结果位才为1 ,否则为0。参与运算的数以补码方式出现。
例如:9&am
- nodejs 数据库连接 mongodb mysql
liguangsong
mongodbmysqlnode数据库连接
1.mysql 连接
package.json中dependencies加入
"mysql":"~2.7.0"
执行 npm install
在config 下创建文件 database.js
- java动态编译
olive6615
javaHotSpotjvm动态编译
在HotSpot虚拟机中,有两个技术是至关重要的,即动态编译(Dynamic compilation)和Profiling。
HotSpot是如何动态编译Javad的bytecode呢?Java bytecode是以解释方式被load到虚拟机的。HotSpot里有一个运行监视器,即Profile Monitor,专门监视
- Storm0.9.5的集群部署配置优化
roadrunners
优化storm.yaml
nimbus结点配置(storm.yaml)信息:
# Licensed to the Apache Software Foundation (ASF) under one
# or more contributor license agreements. See the NOTICE file
# distributed with this work for additional inf
- 101个MySQL 的调节和优化的提示
tomcat_oracle
mysql
1. 拥有足够的物理内存来把整个InnoDB文件加载到内存中——在内存中访问文件时的速度要比在硬盘中访问时快的多。 2. 不惜一切代价避免使用Swap交换分区 – 交换时是从硬盘读取的,它的速度很慢。 3. 使用电池供电的RAM(注:RAM即随机存储器)。 4. 使用高级的RAID(注:Redundant Arrays of Inexpensive Disks,即磁盘阵列
- zoj 3829 Known Notation(贪心)
阿尔萨斯
ZOJ
题目链接:zoj 3829 Known Notation
题目大意:给定一个不完整的后缀表达式,要求有2种不同操作,用尽量少的操作使得表达式完整。
解题思路:贪心,数字的个数要要保证比∗的个数多1,不够的话优先补在开头是最优的。然后遍历一遍字符串,碰到数字+1,碰到∗-1,保证数字的个数大于等1,如果不够减的话,可以和最后面的一个数字交换位置(用栈维护十分方便),因为添加和交换代价都是1
![]() 到复平面的连续映射下的像集,则该点集就称为一条平面曲线,该映射称为该曲线的一个参数方程.按照参数的增大或减小的方向可给出曲线的方向,参数增大的方向为曲线的正方向(默认),参数减小的方向为曲线的反方向.
到复平面的连续映射下的像集,则该点集就称为一条平面曲线,该映射称为该曲线的一个参数方程.按照参数的增大或减小的方向可给出曲线的方向,参数增大的方向为曲线的正方向(默认),参数减小的方向为曲线的反方向. 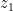 到点
到点 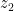 的有向线段
的有向线段 ![z(t)=z_{1}+t(z_{2}-z_{1}),t\in [0,1]](http://img.e-com-net.com/image/info8/aad45ac558994280a1bf187d77d79c14.gif) .
.
![z(\theta )=z_{0}+re^{i\theta },\theta \in [0,2\pi ]](http://img.e-com-net.com/image/info8/cf43d275bb004d29915d7b6858a4757c.gif) 和
和 ![z(\theta )=z_{0}+re^{i\theta },\theta =[0,4\pi ]](http://img.e-com-net.com/image/info8/d18690fcaa374d258231bbcefbb4e5a8.gif) 都表
都表
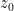 为圆心, 为半径的圆周.
为圆心, 为半径的圆周.
![z(t)=z_{1}+t(z_{2}-z_{1}),t\in [0,1]](http://img.e-com-net.com/image/info8/aad45ac558994280a1bf187d77d79c14.gif) 的切向量.
的切向量.
![]()
![]() .
.![]() 经
经 ![]() 到
到 ![]() 折线段的参数方程
折线段的参数方程 ![z(\theta )=z_{0}+re^{i\theta },\theta \in [0,2\pi ]](http://img.e-com-net.com/image/info8/1e668a0296ed44f8a801d0972ea50950.gif) 的切向量.
的切向量.
![]() .
.![z:[a,b]\rightarrow C](http://img.e-com-net.com/image/info8/a2ab794a2b1948d49bd4918c285f9e2b.gif) ,若存在
,若存在 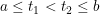 ,使得
,使得 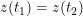 ,则称
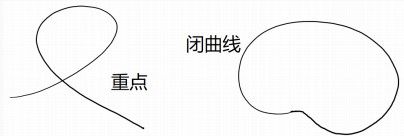
,则称 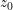 是该参数方程的一个 重(chóng)点 .
是该参数方程的一个 重(chóng)点 .
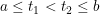 ,都有
,都有 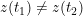 ,或以起点和终点为唯一的重点(即使得
,或以起点和终点为唯一的重点(即使得 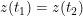 成立的唯一参数值为
成立的唯一参数值为 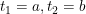 ),则该参数方程描述的曲线称为 简单曲线 (后者称为 简单闭曲线 ).
),则该参数方程描述的曲线称为 简单曲线 (后者称为 简单闭曲线 ).
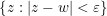 称为点 的 − 邻域 ,记作
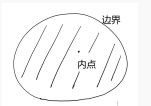
称为点 的 − 邻域 ,记作 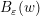 . 定义 对平面点集 中的一点 ,若存在 的 − 邻域
. 定义 对平面点集 中的一点 ,若存在 的 − 邻域 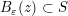 ,则称 是 的 内点 .若 中的所有点都是 的内点,则称 是平面上的 开
,则称 是 的 内点 .若 中的所有点都是 的内点,则称 是平面上的 开
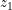 和
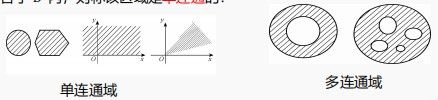
和 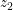 ,都存在落在 中,分别以
,都存在落在 中,分别以 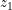 和
和 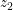 为起点和终点的曲线,则称该集合为 道路连通 的.
为起点和终点的曲线,则称该集合为 道路连通 的.
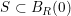 ,则称 为 有界 集.
,则称 为 有界 集.